算法学习记录-查找——平衡二叉树（AVL）

AVL:

本章参考了严蔚敏的《数据结构》，程杰《大话数据结构》

　　上一章的排序二叉树对于我们寻找无序序列中的元素的效率有了大大的提高。查找的最差情况是树的高度。这里就有问题了，将无序数列转化为

二叉排序树的时候，树的结构是非常依赖无序序列的顺序，这样会出现极端的情况。

【如图1】：

　　这样的一颗二叉排序树就是一颗比较极端的情况。我们在查找时候，效率依赖树的高度，所以不希望这样极端情况出现，而是希望元素比较均匀

的分布在根节点两端。

问题提出：

　　能不能有一种方法，使得我们的二叉排序树不依赖无序序列的顺序，也能使得我们得到的二叉排序树是比较均匀的分布。

引入：

　　平衡二叉树（Self-Balancing Binary Search Tree 或 Height-Balanced Binary Search Tree），是一种特殊的二叉排序树，其中每一个结点的

左子树和右子树的高度差至多等于1.

　　这里的平衡从名字中可以看出，Height-Balanced是高度平衡。

　　它或者是一颗空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1.

　　若将二叉树上的结点的平衡因子BF（Balance Factor）定义为该节点的左子树的深度减去它的右子树的深度，则平衡二叉树上所有结点的平衡因子只

可能是-1、0、1。否则就不是平衡二叉树。

　　上图图1中，就不是平衡二叉树。

　　以图1来看看各个结点的平衡因子。

【如下图2】：

如何构成平衡二叉树？

从转化为平衡二叉树的过程中可以提炼出转化的几个基本情况：

下图是在维基百科上摘录的：

可以看出调整的操作分两大类，前两个是一组，后两个是一组，每组之间是对称的。

前两个是对应上图1 2 中情况，

后两个是对应上图5 6 中情况。

分别以其中一种旋转为例，另一种对应的旋转对称。

单次左旋：对应上图1（左左）中情况

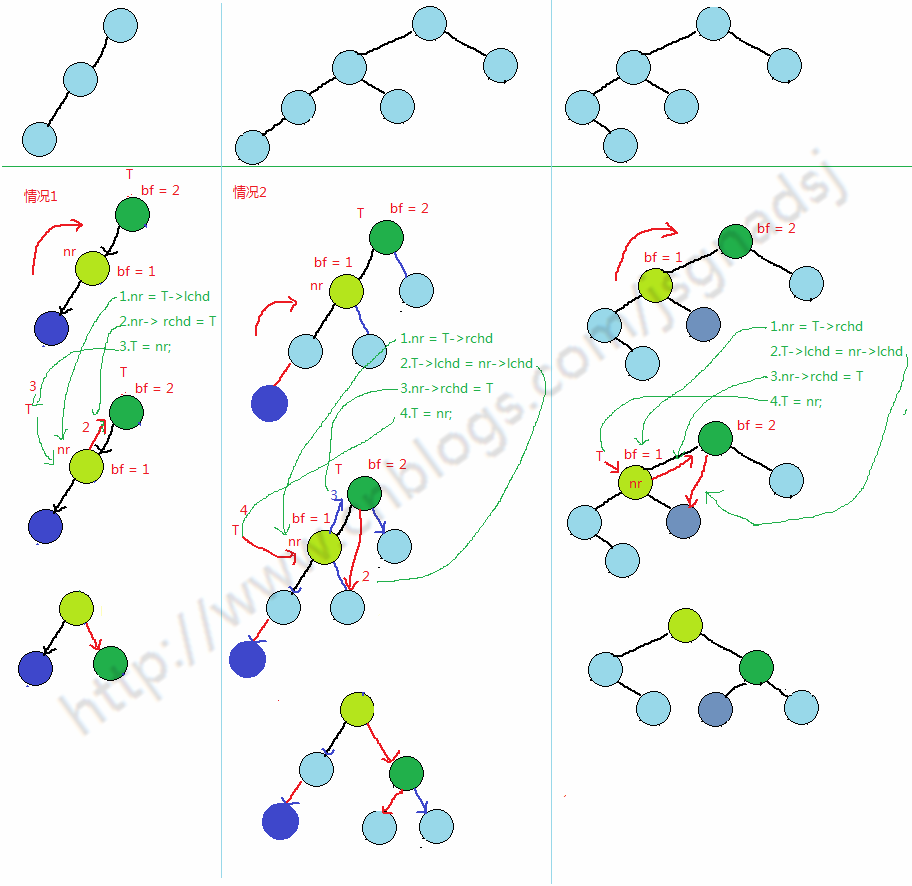
简单左右旋转代码：（只有一次）

 1 void rotateL(pBinTree *p)//左旋转
 2 {
 3     pBinTree r;
 4     r = (*p)->rchd; //r 为新的根
 5     (*p)->rchd = r->lchd;
 6     r->lchd = (*p);
 7     (*p) = r;
 8 }
 9 
10 void rotateR(pBinTree *p)//右旋转
11 {
12     pBinTree r;
13     r = (*p)->lchd; //r 为新的根
14     
15     (*p)->lchd = r->rchd; //新根节点的右孩子附到旧的根结点的左孩子
16     r->rchd = (*p);
17     (*p) = r;
18 }

两次旋转对应图中3（左右）情况

需要旋转两次简单的左右旋转。基于上面代码就可以实现。

为了方便，AVL引入了BF（平衡因子）来调整树。只要出现非平衡树就调整，把不平衡消除最小的情况。

下面就是通过判断BF来实现调整

 1 void BlanceLeft(pBinTree *p)//从最小非平衡树开始调整
 2 {
 3     pBinTree nR,nRchd;
 4     nR = (*p)->lchd;
 5     switch (nR->bf)
 6     {
 7         case LH:    //新插入的结点在左子树
 8         {
 9             (*p)->bf = EH;
10             nR->bf = EH;
11             rotateR(p);
12             break;
13         }
14         case RH:    //新插入的结点在右子树
15         {
16             nRchd = nR->rchd;
17             switch(nRchd->bf)//增加结点是nR的左孩子还是右孩子？
18             {
19                 case LH://
20                 {
21                     (*p)->bf = RH;
22                     nR->bf = EH;
23                     break;
24                 }
25                 case EH://
26                 {
27                     (*p)->bf = EH;
28                     nR->bf = EH;
29                     break;
30                 }
31                 case RH:
32                 {
33                     (*p)->bf = EH;
34                     nR->bf = LH;
35                     break;
36                 }
37             }
38             nRchd->bf = EH;
39             rotateL(&((*p)->lchd));
40             rotateR(p);
41         }
42     }
43 }
44 void BlanceRight(pBinTree *p)//从最小非平衡树开始调整
45 {
46     pBinTree nR,nRchd;
47     nR = (*p)->rchd;
48     
49     switch (nR->bf){
50     case RH:    //新插入的结点在左子树
51         {
52             (*p)->bf = EH;
53             nR->bf = EH;
54             rotateL(p);
55             break;
56         }
57     case LH:    //新插入的结点在右子树
58         {
59             nRchd = nR->lchd;
60             switch(nRchd->bf)//增加结点是nR的左孩子还是右孩子？
61             {
62             case LH://
63                 {
64                     (*p)->bf = EH;
65                     nR->bf = RH;
66                     break;
67                 }
68             case EH://
69                 {
70                     (*p)->bf = EH;
71                     nR->bf = EH;
72                     break;
73                 }
74             case RH:
75                 {
76                     (*p)->bf = LH;
77                     nR->bf = EH;
78                     break;
79                 }
80             }
81             nRchd->bf = EH;
82             rotateR(&((*p)->rchd));
83             rotateL(p);
84         }
85     }
86 }

然后再就是插入算法，这里采用递归的方式插入。

 1 bool InsertAVL(pBinTree *T,int key,bool *taller)
 2 {
 3     if (!*T)
 4     {
 5         *T = (pBinTree)malloc(sizeof(BinTree));
 6         (*T)->data = key;
 7         (*T)->bf   = EH;
 8         (*T)->lchd = NULL;
 9         (*T)->rchd = NULL;
10         *taller = true;
11     }
12     else
13     {
14         if (key  == (*T)->data)
15         {
16             *taller = false;
17             return false;
18         }
19         if (key < (*T)->data)
20         {
21             if (!InsertAVL(&((*T)->lchd),key,taller))
22             {
23                 return false;
24             }
25             if (*taller)
26             {
27                 switch ((*T)->bf)
28                 {
29                 case LH:
30                     {
31                         BlanceLeft(T);
32                         *taller = false;
33                         break;
34                     }
35                 case EH:
36                     {
37                         (*T)->bf = LH;
38                         *taller = true;
39                         break;
40                     }
41                 case RH:
42                     {
43                         (*T)->bf = EH;
44                         *taller = false;
45                         break;
46                     }
47                 }
48 
49             }
50         }
51         else // key > (*T)->data 
52         {
53             if (!InsertAVL(&((*T)->rchd),key,taller))
54             {
55                 return false;
56             }
57             if (*taller)
58             {
59                 switch ((*T)->bf)
60                 {
61                 case LH:
62                     {
63                         (*T)->bf = EH;
64                         *taller = false;
65                         break;
66                     }
67                 case EH:
68                     {
69                         (*T)->bf = RH;
70                         *taller = true;
71                         break;
72                     }
73                 case RH:
74                     {
75                           BlanceRight(T);
76                         *taller = false;
77                         break;
78                     }
79                 }
80 
81             }
82         }
83     }
84     return true;
85 }

以上的代码用switch case 显得非常的繁琐。会导致删除结点的程序判断BF调整非平衡的步骤更多。

以后添加删除部分代码。

完整代码：

  1 // AVL.cpp : 定义控制台应用程序的入口点。
  2 //
  3 
  4 #include "stdafx.h"
  5 #include <stdlib.h>
  6 
  7 #define LH  1
  8 #define EH  0
  9 #define RH -1
 10 
 11 typedef int dataType;
 12 
 13 
 14 typedef struct BinTNode {
 15     dataType data;
 16     int bf;
 17     struct BinTNode *lchd,*rchd;
 18 }BinTree,*pBinTree;
 19 
 20 void rotateL(pBinTree *p)
 21 {
 22     pBinTree r;
 23     r = (*p)->rchd; //r 为新的根
 24     (*p)->rchd = r->lchd;
 25     r->lchd = (*p);
 26     (*p) = r;
 27 }
 28 
 29 void rotateR(pBinTree *p)
 30 {
 31     pBinTree r;
 32     r = (*p)->lchd; //r 为新的根
 33     
 34     (*p)->lchd = r->rchd; //新根节点的右孩子附到旧的根结点的左孩子
 35     r->rchd = (*p);
 36     (*p) = r;
 37 }
 38 
 39 void BlanceLeft(pBinTree *p)//从最小非平衡树开始调整
 40 {
 41     pBinTree nR,nRchd;
 42     nR = (*p)->lchd;
 43     switch (nR->bf)
 44     {
 45         case LH:    //新插入的结点在左子树
 46         {
 47             (*p)->bf = EH;
 48             nR->bf = EH;
 49             rotateR(p);
 50             break;
 51         }
 52         case RH:    //新插入的结点在右子树
 53         {
 54             nRchd = nR->rchd;
 55             switch(nRchd->bf)//增加结点是nR的左孩子还是右孩子？
 56             {
 57                 case LH://
 58                 {
 59                     (*p)->bf = RH;
 60                     nR->bf = EH;
 61                     break;
 62                 }
 63                 case EH://
 64                 {
 65                     (*p)->bf = EH;
 66                     nR->bf = EH;
 67                     break;
 68                 }
 69                 case RH:
 70                 {
 71                     (*p)->bf = EH;
 72                     nR->bf = LH;
 73                     break;
 74                 }
 75             }
 76             nRchd->bf = EH;
 77             rotateL(&((*p)->lchd));
 78             rotateR(p);
 79         }
 80     }
 81 }
 82 void BlanceRight(pBinTree *p)//从最小非平衡树开始调整
 83 {
 84     pBinTree nR,nRchd;
 85     nR = (*p)->rchd;
 86     
 87     switch (nR->bf){
 88     case RH:    //新插入的结点在左子树
 89         {
 90             (*p)->bf = EH;
 91             nR->bf = EH;
 92             rotateL(p);
 93             break;
 94         }
 95     case LH:    //新插入的结点在右子树
 96         {
 97             nRchd = nR->lchd;
 98             switch(nRchd->bf)//增加结点是nR的左孩子还是右孩子？
 99             {
100             case LH://
101                 {
102                     (*p)->bf = EH;
103                     nR->bf = RH;
104                     break;
105                 }
106             case EH://
107                 {
108                     (*p)->bf = EH;
109                     nR->bf = EH;
110                     break;
111                 }
112             case RH:
113                 {
114                     (*p)->bf = LH;
115                     nR->bf = EH;
116                     break;
117                 }
118             }
119             nRchd->bf = EH;
120             rotateR(&((*p)->rchd));
121             rotateL(p);
122         }
123     }
124 }
125 
126 bool InsertAVL(pBinTree *T,int key,bool *taller)
127 {
128     if (!*T)
129     {
130         *T = (pBinTree)malloc(sizeof(BinTree));
131         (*T)->data = key;
132         (*T)->bf   = EH;
133         (*T)->lchd = NULL;
134         (*T)->rchd = NULL;
135         *taller = true;
136     }
137     else
138     {
139         if (key  == (*T)->data)
140         {
141             *taller = false;
142             return false;
143         }
144         if (key < (*T)->data)
145         {
146             if (!InsertAVL(&((*T)->lchd),key,taller))
147             {
148                 return false;
149             }
150             if (*taller)
151             {
152                 switch ((*T)->bf)
153                 {
154                 case LH:
155                     {
156                         BlanceLeft(T);
157                         *taller = false;
158                         break;
159                     }
160                 case EH:
161                     {
162                         (*T)->bf = LH;
163                         *taller = true;
164                         break;
165                     }
166                 case RH:
167                     {
168                         (*T)->bf = EH;
169                         *taller = false;
170                         break;
171                     }
172                 }
173 
174             }
175         }
176         else // key > (*T)->data 
177         {
178             if (!InsertAVL(&((*T)->rchd),key,taller))
179             {
180                 return false;
181             }
182             if (*taller)
183             {
184                 switch ((*T)->bf)
185                 {
186                 case LH:
187                     {
188                         (*T)->bf = EH;
189                         *taller = false;
190                         break;
191                     }
192                 case EH:
193                     {
194                         (*T)->bf = RH;
195                         *taller = true;
196                         break;
197                     }
198                 case RH:
199                     {
200                           BlanceRight(T);
201                         *taller = false;
202                         break;
203                     }
204                 }
205 
206             }
207         }
208     }
209     return true;
210 }
211 
212 
213 int _tmain(int argc, _TCHAR* argv[])
214 {
215     int a[10] = {2,1,0,3,4,6,7,9,8,5};
216     int i;
217     bool taller;
218     pBinTree T = NULL;
219 
220     for (i=0;i<10;i++)
221     {
222         InsertAVL(&T,a[i],&taller);
223     }
224     getchar();
225     return 0;
226 }

以上代码经过测试，可以使用。

posted @ 2013-12-17 13:58 sjdang 阅读(748) 评论(0) 编辑收藏举报

刷新页面返回顶部

算法学习记录-查找——平衡二叉树（AVL）

公告