强化学习 1 --- 马尔科夫决策过程详解(MDP)
强化学习 --- 马尔科夫决策过程(MDP)
1、强化学习介绍
强化学习任务通常使用马尔可夫决策过程(Markov Decision Process,简称MDP)来描述,具体而言:机器处在一个环境中,每个状态为机器对当前环境的感知;机器只能通过动作来影响环境,当机器执行一个动作后,会使得环境按某种概率转移到另一个状态;同时,环境会根据潜在的奖赏函数反馈给机器一个奖赏。综合而言,强化学习主要包含四个要素:状态、动作、转移概率以及奖赏函数。
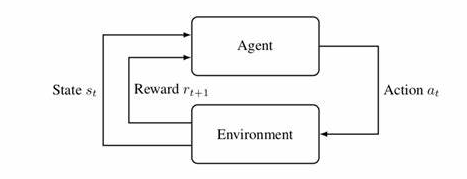
根据上图,agent(智能体)在进行某个任务时,首先与environment进行交互,产生新的状态state,同时环境给出奖励reward,如此循环下去,agent和environment不断交互产生更多新的数据。强化学习算法就是通过一系列动作策略与环境交互,产生新的数据,再利用新的数据去修改自身的动作策略,经过数次迭代后,agent就会学习到完成任务所需要的动作策略。
2、马尔科夫过程(Markov Process)
马尔可夫性当前状态包含了对未来预测所需要的有用信息,过去信息对未来预测不重要,该就满足了马尔科夫性,严格来说,就是某一状态信息包含了所有相关的历史,只要当前状态可知,所有的历史信息都不再需要,当前状态就可以决定未来,则认为该状态具有马尔科夫性。用公式描述为:
马尔科夫过程又叫做马尔科夫链(Markov Chain),它是一个无记忆的随机过程,可以用一个元组<S, P>表示,其中
S是有限数量的状态集 \(S ={s_1, s_2, s_3, \cdots, s_t}\)P是状态转移概率矩阵 \(p(S_{t+1} = s'|s_t=s) \;\) 其中 \(s'\) 表示下一时刻的状态,\(s\) 表示当前状态
如下如所示:对于状态\(s_1\)来说,有0.1的概率保持不变,有0.2的概率转移到\(s_2\)状态,有0.7的概率转移到\(s_4\)状态。
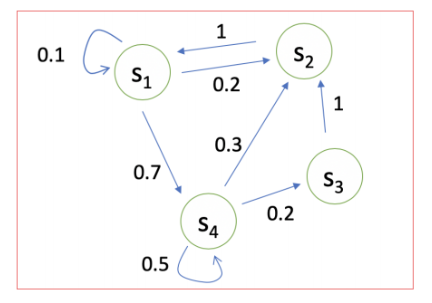
我们可以使用矩阵来表示:
3、马尔科夫奖励过程(Markov Reward Process)
3.1、概念介绍
马尔科夫奖励过程是在马尔科夫过程基础上增加了奖励函数 \(R\) 和衰减系数 \(\gamma\), 用 \(<S, R,P, \gamma>\)表示
- \(R\) : 表示 \(S\) 状态下某一时刻的状态\(S_t\) 在下一个时刻 \((t + 1)\) 能获得的奖励的期望
- \(G_t\) : 收获 \(G_t\)为在一个马尔科夫奖励链上从t时刻开始往后所有的奖励的有衰减的收益总和
- \(\gamma\) : 折扣因子\((Discount \; factor γ ∈ [0, 1])\)
- 1、为了避免出现状态循环的情况
- 2、系统对于将来的预测并不一定都是准确的,所以要打折扣
- 很显然
越靠近1,考虑的利益越长远。
- \(V(s)\) : 状态价值函数(state value function) 表示从从该状态开始的马尔科夫链收获\(G_t\)的期望
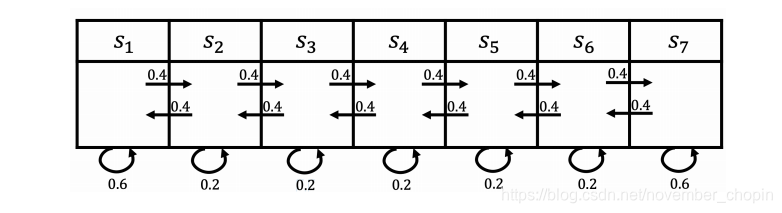
例子:对于如下状态,我们设定进入 \(S_1\) 状态奖励为 5,进入\(S_7\) 状态奖励为 10,其余状态奖励为 0。则\(R\)可以如下表示:\(R = [5,0,0,0,0,0,10]\) ,折扣 因子 \(\gamma\) 为 0.5。则对于下面两个马尔可夫过程获得的奖励为:
- $S_4, S_5, S_6, S_7: $ 0 + 0.5*0 + 0.5*0 + 0.125 *10 = 1.25
- \(S_4,S_3,S_2,S_1\) : 0 + 0.5 ×0 + 0.25×0 + 0.125×5 = 0.625
3.2、Bellman Equation 贝尔曼方程
\(v(s) = E[G_t|S_t = s]\)
\(= E[R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots|S_t = s]\)
\(= E[R_{t+1} + \gamma(R_{t+2} + R_{t+3} + \cdots)|S_t=s]\)
\(=E[R_{t+1} + \gamma v(S_{t+1})|S_t = s]\)
\(=\underbrace{E[R_{t+1}|S_t=s]}_{当前的奖励} + \underbrace{\gamma E[v(S_{t+1})|S_t = s]}_{下一时刻状态的价值期望}\)
使用贝尔曼方程状态价值\(V\)可以表示为:
S 表示下一时刻的所有状态,s' 表示下一时刻可能的状态
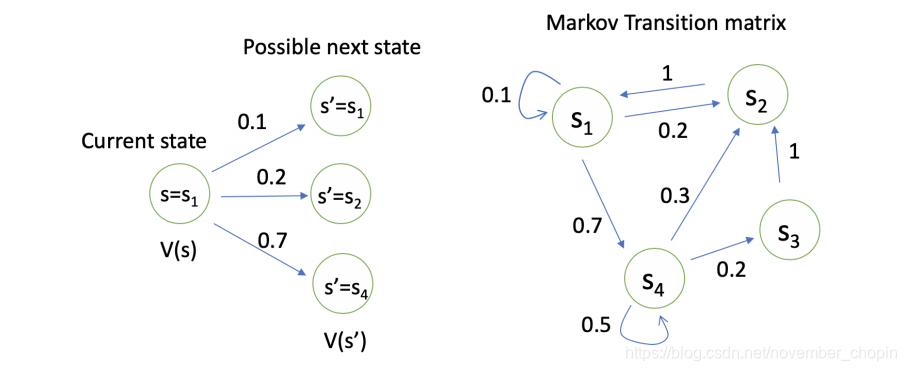
通过贝尔曼方程,可以看到价值函数\(v(s)\)有两部分组成,一个是当前获得的奖励的期望,即\(R(s)\),另一个是下一时刻的状态期望,即下一时刻 可能的状态能获得奖励期望与对应状态转移概率乘积的和,最后在加上折扣。如下图所示,对于状态 \(s_1\),它的价值函数为:\(V(s_1) = R(s_1) + \gamma(0.1*V(s_1) + 0.2*V(s_2) + 0.7*V(s_4))\)
4、马尔科夫决策过程(Markov Decision Process)
马尔科夫决策过程是在马尔科夫奖励过程的基础上加了 Decision 过程,相当于多了一个动作集合,可以用 \(<S, A, P, R, \gamma>\),这里的 P 和 R 都与具体的行为 a 对应,而不像马尔科夫奖励过程那样仅对应于某个状态。
-
\(A\) 表示有限的行为集合
-
\(S\)表示有限的状态集合
-
\(P^a\) is dynamics / transition model for each action
\[P(s_{t+1} = s'|s_t = s, a_t = a) = P[S_{t+1}=s'|S_t = s, A_t = a] \] -
\(R\) 是奖励函数 \(R(s_t=s, a_t = a) = E[R_t|s_t=s, a_t=a]\)
4.1、策略 (Policy)
用 \(\pi\) 表示策略的集合,其元素 \(\pi(a|s)\) 表示某一状态 s 采取可能的行为 a 的概率
这里需要注意的是:
- Policy定义完整定义的个体行为方式,即包括了个体在各状态下的所有行为和概率
- 同时某一确定的Policy是静态的,与时间无关
- Policy仅和当前的状态有关,与历史信息无关,但是个体可以随着时间更新策略
在马尔科夫奖励过程中 策略 \(\pi\) 满足以下方程,可以参照下面图来理解
状态转移概率可以描述为:在执行策略 \(\pi\) 时,状态从 s 转移至 s' 的概率等于执行该状态下所有行为的概率与对应行为能使状态从 s 转移至 s’ 的概率的乘积的和。参考下图
奖励函数可以描述为:在执行策略 \(\pi\) 时获得的奖励等于执行该状态下所有行为的概率与对应行为产生的即时奖励的乘积的和。
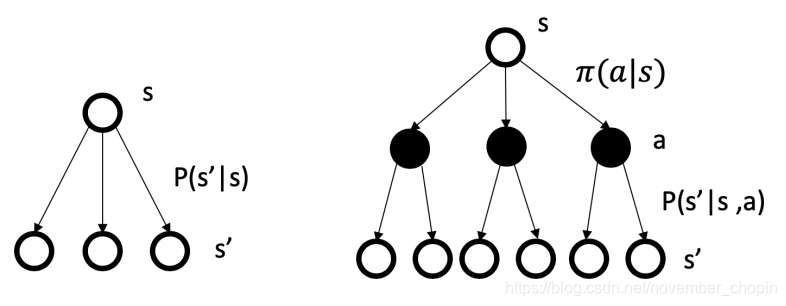
我们引入策略,也可以理解为行动指南,更加规范的描述个体的行为,既然有了行动指南,我们要判断行动指南的价值,我们需要再引入基于策略的价值函数。
基于策略的状态价值函数(state value function)
- \(V(s)\) 表示从状态 \(s\) 开始,遵循当前策略时所获得的收获的期望
其中 \(G_t\) 可以参照马科夫奖励过程。我们有了价值衡量标准,如果状态 s 是一个好的状态,如何选择动作到达这个状态,这时就需要判断动作的好坏,衡量行为价值。
基于策略的行为价值函数(action value function)
- \(q_{\pi}(s,a)\)当前状态s执行某一具体行为a所能的到的收获的期望
- 根据 Bellman 公式推导可得(参照马尔科夫奖励过程中 V 的推导)
在某一个状态下采取某一个行为的价值,可以分为两部分:其一是离开这个状态的价值,其二是所有进入新的状态的价值于其转移概率乘积的和。参考下图右理解
- 由状态价值函数和行为价值函数的定义,可得两者的关系
我们知道策略就是用来描述各个不同状态下执行各个不同行为的概率,而状态价值是遵循当前策略时所获得的收获的期望,即状态 s 的价值体现为在该状态下遵循某一策略而采取所有可能行为的价值按行为发生概率的乘积求和。参照下图左理解
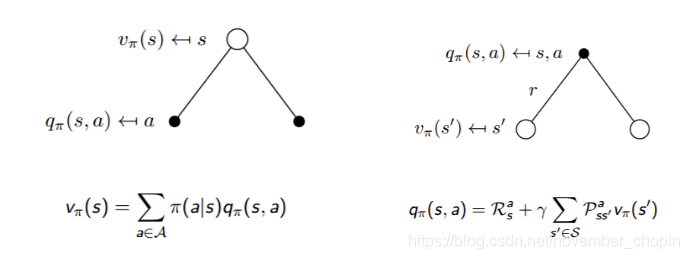
- 上面两个公式组合可得 Bellman Expectation Equation
5、最优价值函数
解决强化学习问题意味着要寻找一个最优的策略让个体在与环境交互过程中获得始终比其它策略都要多的收获,这个最优策略我们可以用 \(\pi_*\) 表示。一旦找到这个最优策略\(\pi_*\) ,那么我们就解决了这个强化学习问题。一般来说,比较难去找到一个最优策略,但是可以通过比较若干不同策略的优劣来确定一个较好的策略,也就是局部最优解。
我们一般是通过对应的价值函数来比较策略的优劣,也就是说,寻找较优策略可以通过寻找较优的价值函数来完成。可以定义最优状态价值函数是所有策略下产生的众多状态价值函数中的最大者,即:
同理也可以定义最优动作价值函数是所有策略下产生的众多动作状态价值函数中的最大者,即:
我们可以最大化最优行为价值函数找到最优策略:
Bellman Optimality Equation
只要我们找到了最大的状态价值函数或者动作价值函数,那么对应的策略 \(\pi_*\) 就是我们强化学习问题的解。同时,利用状态价值函数和动作价值函数之间的关系,我们也可以得到:
当到达 最优的时候,一个状态的价值就等于在当前 状态下最大的那个动作价值
把上面两个式子结合起来有Bellman Optimality Equation
6、MDP 实例
下面给出一个例子,希望能能好的理解MDP过程
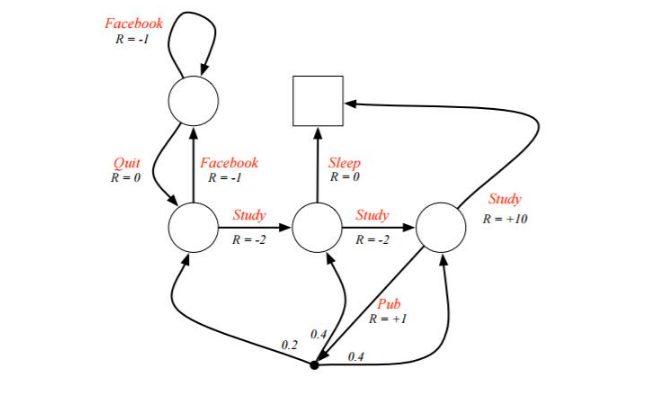
例子是一个学生学习考试的MDP。里面左下那个圆圈位置是起点,方框那个位置是终点。上面的动作有study, pub, facebook, quit, sleep,每个状态动作对应的即时奖励R已经标出来了。我们的目标是找到最优的动作价值函数或者状态价值函数,进而找出最优的策略。
为了方便,我们假设衰减因子 $\gamma = 1, \quad \pi(a|s)=0.5 $
对于终点方框位置,由于其没有下一个状态,也没有当前状态的动作,因此其状态价值函数为0。对于其余四个状态,我们依次定义其价值为\(v_1, v_2, v_3, v_4\) 分别对应左上,左下,中下,右下位置的圆圈。我们基于
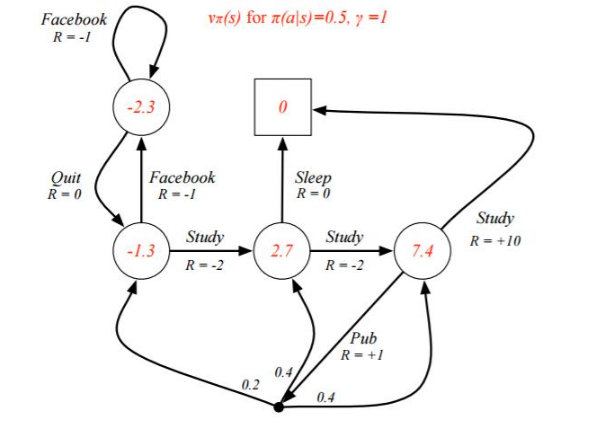
来计算所有状态的价值函数,可以得到如下方程组
- 对于 v_1: \(v_1 = 0.5 * (-1 + v_1) + 0.5 * (0 + v_2)\)
- 对于 v_2: \(v_2 = 0.5 * (-1 + v_1) + 0.5 * (-2 + v_3)\)
- 对于 v_3: \(v_3 = 0.5 * (0+0) + 0.5 * (-2 + v_4)\)
- 对于 v_4: \(v_4 = 0.5 * (10+0) + 0.5 * (1 + 0.2 * v_2 + 0.4 * v_3 + 0.4 * v_4)\)
解这个方程组可得:\(v_1 = -2.3, v_2 = -1.3, v_3 = 2.7, v_4 = 7.4\) 既是每个状态的价值函数
上面我们固定了策略\(π(a|s)π(a|s),\)虽然求出了每个状态的状态价值函数,但是却并不一定是最优价值函数。那么如何求出最优价值函数呢?这里由于状态机简单,求出最优的状态价值函数 \(v_*(s)\) 或者动作价值函数 \(q_*(s)\) 比较容易。
我们这次以动作价值函数\(q_*(s)\) 来为例求解。然后我们按照下面公式,
可以得到下面等式
然后求出所有的 \(q_*(s,a)\) ,然后再 利用 \(v_*(s, a) = max_aq_*(s,a)\) 就可以求出所有的 \(v_*(s)\) ,最终结果如下图所示
7、MDP 小结
虽然MDP可以直接用方程组求解简单的问题,但是却不能解决复杂的问题,因此我们需要寻找其他的方法来求解
下篇文章使用动态规划方法来解决 MDP问题,涉及到 Policy Iteration 和 Value Iteration 两个算法,还请大家多多关注。
本篇文章是我的强化学习开篇之作,如果觉得文章写的不错,还请各位看官老爷点赞收藏加关注啊,后面会一直写下去的,再此谢谢啦
参考资料:
- B站 周老师强化学习纲要第二讲上
- 博客园
![返回主页]() 刘建平Pinard
刘建平Pinard


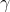 越靠近1,考虑的利益越长远。
越靠近1,考虑的利益越长远。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号