tarjan求割边割点
tarjan求割边割点
内容及代码来自http://m.blog.csdn.net/article/details?id=51984469
割边:在连通图中,删除了连通图的某条边后,图不再连通。这样的边被称为割边,也叫做桥。
割点:在连通图中,删除了连通图的某个点以及与这个点相连的边后,图不再连通。这样的点被称为割点。
DFS搜索树:用DFS对图进行遍历时,按照遍历次序的不同,我们可以得到一棵DFS搜索树。
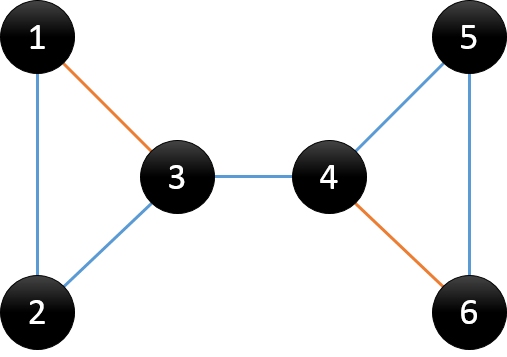
树边:在搜索树中的蓝色线所示,可理解为在DFS过程中访问未访问节点时所经过的边,也称为父子边
回边:在搜索树中的橙色线所示,可理解为在DFS过程中遇到已访问节点时所经过的边,也称为返祖边、后向边
观察DFS搜索树,我们可以发现有两类节点可以成为割点。对根节点u,若其有两棵或两棵以上的子树,则该根结点u为割点;对非叶子节点u(非根节点),若其中的某棵子树的节点均没有指向u的祖先节点的回边,说明删除u之后,根结点与该棵子树的节点不再连通;则节点u为割点。对于根结点,显然很好处理;但是对于非叶子节点,怎么去判断有没有回边是一个值得深思的问题。我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号,low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小),那么low[u]的计算过程如下。
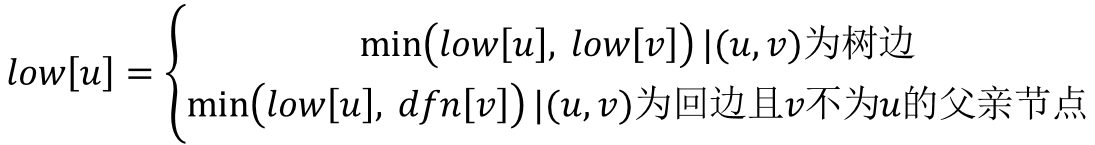
对于给的例子,其求出的dfn和low数组如下。
id 123456
dfn 123456
low 111444
可以发现,对于情况2,当(u,v)为树边且low[v]≥dfn[u]时,节点u才为割点。而当(u,v)为树边且low[v]>dfn[u]时,表示v节点只能通过该边(u,v)与u连通,那么(u,v)即为割边。tarjan算法的时间复杂度是O(n+m)的,非常快。
以hihoCoder1183为例给出代码:

1 #include<cstdio> 2 #include<vector> 3 #include<algorithm> 4 using namespace std; 5 int n,m,order=0; 6 int low[20004],dfn[20004],father[20004],son[20004]; 7 //father:父结点 son:子结点个数 8 vector<int> cutpoint,edge[20004]; 9 vector< pair<int,int> > cutedge; 10 11 void tarjan(int u) 12 { 13 dfn[u]=low[u]=++order; 14 bool flag=false; 15 for (int i=0;i<edge[u].size();i++) 16 { 17 int v=edge[u][i]; 18 if(!dfn[v]) 19 { 20 son[u]++; 21 father[v]=u; 22 tarjan(v); 23 if(low[v]>=dfn[u]) flag=true; 24 //点u为割点 25 if(low[v]>dfn[u]) cutedge.push_back(make_pair(min(v,u),max(v,u))); 26 //边v-u为割边 27 low[u]=min(low[u],low[v]); 28 } 29 else if(v!=father[u]) low[u]=min(low[u],dfn[v]); 30 } 31 //根节点若有两棵或两棵以上的子树则该为割点 32 //非根节点若所有子树节点均没有指向u的祖先节点的回边则为割点 33 if((father[u]==0&&son[u]>1)||(father[u]&&flag)) cutpoint.push_back(u); 34 } 35 36 int main() 37 { 38 scanf("%d%d",&n,&m); 39 for (int i=1;i<=m;i++) 40 { 41 int u,v; 42 scanf("%d%d",&u,&v); 43 edge[u].push_back(v),edge[v].push_back(u); 44 } 45 tarjan(1); 46 sort(cutedge.begin(),cutedge.end()); 47 sort(cutpoint.begin(),cutpoint.end()); 48 if(0==cutpoint.size()) puts("Null"); 49 else 50 { 51 printf("%d",cutpoint[0]); 52 for (int i=1;i<cutpoint.size();i++) printf(" %d",cutpoint[i]); 53 puts(""); 54 } 55 for(int i=0;i<cutedge.size();i++) printf("%d %d\n",cutedge[i].first,cutedge[i].second); 56 }
不过话说一整篇博客,光复制别人的东西不大好,那我就上一个自己打的链表实现的代码:

1 #include<cstdio> 2 #include<vector> 3 #include<algorithm> 4 #define N 420000 5 using namespace std; 6 vector<int>cutpoint; 7 vector<pair<int,int> >cutedge; 8 int next[N],to[N],num,head[N],dfn[N],low[N],tim,son[N],father[N],n,m,a,b; 9 bool flag; 10 void add(int false_from,int false_to){ 11 next[++num]=head[false_from]; 12 to[num]=false_to; 13 head[false_from]=num; 14 } 15 void dfs(int x){ 16 dfn[x]=low[x]=++tim; 17 bool flag=0; 18 for(int i=head[x];i;i=next[i]){ 19 if(!dfn[to[i]]){ 20 son[x]++; 21 father[to[i]]=x; 22 dfs(to[i]); 23 if(low[to[i]]>=dfn[x]) 24 flag=1; 25 if(low[to[i]]>dfn[x]) 26 cutedge.push_back(make_pair(min(x,to[i]),max(x,to[i]))); 27 low[x]=min(low[x],low[to[i]]); 28 } 29 else 30 if(father[x]!=to[i]) 31 low[x]=min(low[x],dfn[to[i]]); 32 } 33 if((!father[x]&&son[x]>1)||(father[x]&&flag)) 34 cutpoint.push_back(x); 35 } 36 int main(){ 37 scanf("%d%d",&n,&m); 38 for(int i=1;i<=m;++i){ 39 scanf("%d%d",&a,&b); 40 add(a,b); 41 add(b,a); 42 } 43 dfs(1); 44 sort(cutpoint.begin(),cutpoint.end()); 45 sort(cutedge.begin(),cutedge.end()); 46 printf("%d",cutpoint[0]); 47 for(int i=1;i<cutpoint.size();i++) 48 printf(" %d",cutpoint[i]); 49 printf("\n"); 50 for(int i=0;i<cutedge.size();i++) 51 printf("%d %d\n",cutedge[i].first,cutedge[i].second); 52 return 0; 53 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号