tarjan算法求LCA
tarjan算法求LCA
LCA（Least Common Ancestors）的意思是最近公共祖先，即在一棵树中，找出两节点最近的公共祖先。
这里我们使用tarjan算法离线算法解决这个问题。
离线算法，是指首先读入所有的询问（求一次LCA叫做一次询问），然后重新组织查询处理顺序以便得到更高效的处理方法。Tarjan算法是一个常见的用于解决LCA问题的离线算法，它结合了深度优先遍历和并查集，整个算法为线性处理时间。
总思路就是每进入一个节点u的深搜，就把整个树的一部分看作以节点u为根节点的小树，再搜索其他的节点。每搜索完一个点后，如果该点和另一个已搜索完点为需要查询LCA的点，则这两点的LCA为另一个点的现在的祖先。
1.先建立两个链表，一个为树的各条边，另一个是需要查询最近公共祖先的两节点。
2.建好后，从根节点开始进行一遍深搜。
3.先把该节点u的father设为他自己（也就是只看大树的一部分，把那一部分看作是一棵树），搜索与此节点相连的所有点v，如果点v没被搜索过，则进入点v的深搜，深搜完后把点v的father设为点u。
4.深搜完一点u后，开始判断节点u与另一节点v是否满足求LCA的条件，满足则将结果存入数组中。
5.搜索完所有点，自动退出初始的第一个深搜，输出结果。
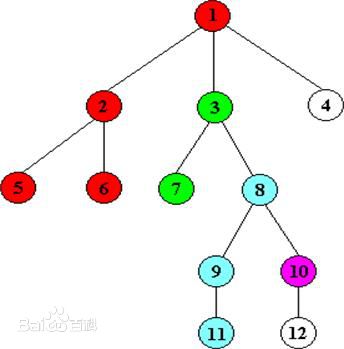
如上图，根据实现算法可以看出，只有当某一棵子树全部遍历处理完成后，才将该子树的根节点标记为有颜色（初始化是白色），假设程序按上面的树形结构进行遍历，首先从节点1开始，然后递归处理根为2的子树，当子树2处理完毕后，节点2， 5， 6均为红色；接着要回溯处理3子树，首先被染色的是节点7（因为节点7作为叶子不用深搜，直接处理），接着节点7就会查看所有询问(7, x)的节点对，假如存在(7, 5)，因为节点5已经被染黑，所以就可以断定(7, 5)的最近公共祖先就是find(5)，即节点1（因为2子树处理完毕后，子树2和节点1返回了合并后的树的根1，此时树根的祖先的值就是1）。
代码实现：
1 #include<cstdio> 2 #define N 420000 3 struct hehe{ 4 int next; 5 int to; 6 int lca; 7 }; 8 hehe edge[N];//树的链表 9 hehe qedge[N];//需要查询LCA的两节点的链表 10 int n,m,p,x,y; 11 int num_edge,num_qedge,head[N],qhead[N]; 12 int father[N]; 13 int visit[N];//判断是否被找过 14 void add_edge(int from,int to){//建立树的链表 15 edge[++num_edge].next=head[from]; 16 edge[num_edge].to=to; 17 head[from]=num_edge; 18 } 19 void add_qedge(int from,int to){//建立需要查询LCA的两节点的链表 20 qedge[++num_qedge].next=qhead[from]; 21 qedge[num_qedge].to=to; 22 qhead[from]=num_qedge; 23 } 24 int find(int z){//找爹函数 25 if(father[z]!=z) 26 father[z]=find(father[z]); 27 return father[z]; 28 } 29 int dfs(int x){//把整棵树的一部分看作以节点x为根节点的小树 30 father[x]=x;//由于节点x被看作是根节点，所以把x的father设为它自己 31 visit[x]=1;//标记为已被搜索过 32 for(int k=head[x];k;k=edge[k].next)//遍历所有与x相连的节点 33 if(!visit[edge[k].to]){//若未被搜索 34 dfs(edge[k].to);//以该节点为根节点搞小树 35 father[edge[k].to]=x;//把x的孩子节点的father重新设为x 36 } 37 for(int k=qhead[x];k;k=qedge[k].next)//搜索包含节点x的所有询问 38 if(visit[qedge[k].to]){//如果另一节点已被搜索过 39 qedge[k].lca=find(qedge[k].to);//把另一节点的祖先设为这两个节点的最近公共祖先 40 if(k%2)//由于将每一组查询变为两组，所以2n-1和2n的结果是一样的 41 qedge[k+1].lca=qedge[k].lca; 42 else 43 qedge[k-1].lca=qedge[k].lca; 44 } 45 } 46 int main(){ 47 scanf("%d%d%d",&n,&m,&p);//输入节点数，查询数和根节点 48 for(int i=1;i<n;++i){ 49 scanf("%d%d",&x,&y);//输入每条边 50 add_edge(x,y); 51 add_edge(y,x); 52 } 53 for(int i=1;i<=m;++i){ 54 scanf("%d%d",&x,&y);//输入每次查询，考虑(u,v)时若查找到u但v未被查找，所以将(u,v)(v,u)全部记录 55 add_qedge(x,y); 56 add_qedge(y,x); 57 } 58 dfs(p);//进入以p为根节点的树的深搜 59 for(int i=1;i<=m;i++) 60 printf("%d ",qedge[i*2].lca);//两者结果一样，只输出一组即可 61 return 0; 62 }
时间复杂度：O(n+m)。
离线算法。
