欧拉稀疏表示解决图像分类
核技巧可以捕获特征间非线性相似性,从而提高不同类别数据可分性。受此启发,本文提出了Euler SRC算法:首先用欧拉表示将图像映射到复数空间,再执行复数SRC算法。实验表明Euler SRC在图像分类上性能优于传统SRC。
题目:Euler Sparse Representation for Image Classification, 2018
作者:Yang Liu,西安电子科技大学
链接:https://ojs.aaai.org/index.php/AAAI/article/view/11670/11529

SRC
该类方法假定同一个类别的图像共处一个子空间中,所以对于任意测试样本 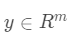 ,都可以认为近似处于训练集中和 y 有相同类标签的样本生成的空间里。假设
,都可以认为近似处于训练集中和 y 有相同类标签的样本生成的空间里。假设 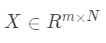 是从
是从 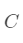 类中采样得到的训练集,那么 y 可以被表示为所有训练集样本的线性组合,相应的系数向量
类中采样得到的训练集,那么 y 可以被表示为所有训练集样本的线性组合,相应的系数向量 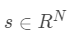 可通过解如下目标函数得到
可通过解如下目标函数得到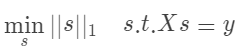
其中 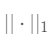 表示
表示 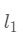 范数,计算向量中每个分量的模的和。
范数,计算向量中每个分量的模的和。
目标函数 (1) 表明 y 可以被精确表示。但实际应用中,由于数据有噪音,y 不可能精确地表示为样本的稀疏叠加。所以,目标函数 (1) 修改为
通过目标函数 (2) 得到系数向量 s 后,SRC根据残差对测试样本 y 进行分类。具体来说,对类别 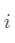 ,
,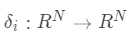 是选择与第
是选择与第 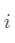 类关联的系数的特征函数。
类关联的系数的特征函数。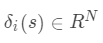 是一个新向量,其唯一的非零项是 s 中与类
是一个新向量,其唯一的非零项是 s 中与类 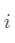 相关的项。将 y 归于第
相关的项。将 y 归于第 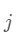 类,如果下式成立
类,如果下式成立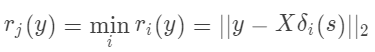
易见得SRC在图像识别方面实现了良好的性能,尤其是对于有遮挡的图片。目标函数 (2) 中第一项采用平方 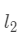 范数作为距离指标。众所周知,在平方
范数作为距离指标。众所周知,在平方 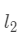 范数意义下,相同类别的图片在不同光照和时间下的变化甚至比不同类别图像间的差异还要大,这影响了SRC的鲁棒性和灵活性。为了解决这个问题,我们在下一节引入了Euler SRC。
范数意义下,相同类别的图片在不同光照和时间下的变化甚至比不同类别图像间的差异还要大,这影响了SRC的鲁棒性和灵活性。为了解决这个问题,我们在下一节引入了Euler SRC。
Euler SRC
动机
定义1 对于两个随机向量 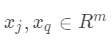 ,它们间的余弦距离指标如下:
,它们间的余弦距离指标如下:
相比于欧氏距离,余弦距离可以同时扩大类内和类间间距,但类间间距扩大的倍数更大。AR数据集上的实验验证了这点(见下图),图中包括样本A,和样本A有相同类别属性的四个最近的样本B、C、D、E,和样本A有不同类别属性的四个最近的样本F、G、H、K。可以看到,margin被扩大了数十倍。

对 (4) 做变换如下: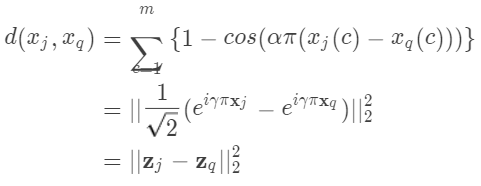
我们称 (6) 为 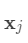 的欧拉表示(Euler representation),
的欧拉表示(Euler representation),
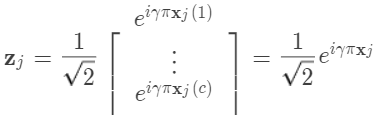
式 (5) 表明像素空间中的余弦距离和欧拉映射空间中相应的 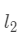 范数距离相同,而且2范距离更加容易求解优化问题。所以我们的方法首先将图像映射到复空间中,再在欧拉空间中执行复SRC算法。
范数距离相同,而且2范距离更加容易求解优化问题。所以我们的方法首先将图像映射到复空间中,再在欧拉空间中执行复SRC算法。
算法流程
输入 训练样本 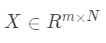 ,参数
,参数 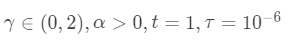 .
.
初始化 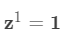 .
.
流程
将
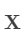 映射到 [0,1]中.
映射到 [0,1]中.计算
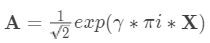 .
.计算
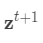 通过 (7).
通过 (7).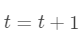 ,继续步骤3,直到
,继续步骤3,直到 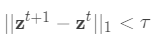 .
.返回
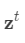 .
.
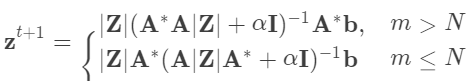
其中 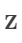 是
是 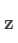 中元素组成的对角方阵,即
中元素组成的对角方阵,即 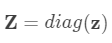 。
。
实验
4个数据集:COIL20, AR, PIE和LFWcrop
对比模型:SRC(Wright等人,2009)、RSR(Riemannian Sparse Representation)(Harandi等人,2012)
实验中,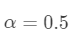 ,每种方法都分别选择PCA和降采样作为预处理过程,PCA降到200维。Euler SRC中,
,每种方法都分别选择PCA和降采样作为预处理过程,PCA降到200维。Euler SRC中,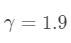 。
。
人脸识别实验
AR数据集包括超过4000张彩色人脸图像,由126个人不同的面部表情、光照条件、遮挡的正面照组成。120个人(65个男人,55个女人)的照片分为两部分(相隔两周)。每一部分包含13张彩色图像,6张是遮挡的,7张是不同面部表情和光照的。实验中,我们手动裁剪出图像中的人脸并将其归一化到 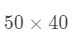 像素。下图展示了某人归一化后的一些图像。我们在这个数据集上做了三组实验。
像素。下图展示了某人归一化后的一些图像。我们在这个数据集上做了三组实验。

实验一:我们考虑戴墨镜的训练图像。我们选用面部图像(a)-(g)和图像(h)进行训练,剩下的所有面部图像和含墨镜的图像做测试集,其中包括来自session 1的2张图像和来自session 2的3张图像。综上所述,我们有960张训练图像和1440张测试图像。
实验二:我们考虑对围巾遮挡图像进行图像分类,被遮挡区域约有40%。实验中,我们选择每个人的图像(a)-(g)和图像(k)进行训练,剩下的所有面部图像和含围巾的图像做测试集。同样有960个训练样本和1440个测试样本。
实验三:我们考虑墨镜和围巾遮挡图像做图像分类,被遮挡区域大概40%。实验中,我们选择每人从(a)-(g)7个全脸图像和(h)(k) 两个坏图像进行训练,剩余图像用作测试。同样有1080个训练样本和2040个测试样本。

表3和表4列出了AR数据集上平均识别率和标准偏差。
COIL20数据集(Nene等人,1996)包括20个目标共1440张彩色图像(每个目标72张)。这些目标有着复杂的几何和反射特征。这个数据库称为哥伦比亚物体图像库(COIL-20),用于含20对象的实时识别系统。将每个对象放置在转盘中心附近的稳定位置,然后转盘旋转360度,每个对象共拍72张图片,每次旋转5度。图3中展示了一些样本图像。我们从每个对象中随机选择10张图像用于训练,剩余的图像用于测试。所有试验重复10次。

CMU PIE(Sim, Baker, 和Bsat 2002)包括68个对象共41368张图像。在43种不同的光照情况、4个不同的表情情况下,采用13个同步摄像头和21个闪光灯拍摄人脸照片。实验中,我们选择C05姿势(近乎正面的姿势)作为相册,其中包括68个人,每人49张图像。所有图像都人工对齐、裁剪并resize到64*64.图4中展示了一些样本。每个类别中我们随机选择7张图像用于训练,剩余图像用于测试。所有实验都重复10次。

LFWCrop数据集(Sanderson和Lovell 2009)是LFW数据集(Huang等人,2007)的一个裁剪版本,在绝大多数图像中,几乎所有背景都被省略,然后将提取的区域缩放为64x64像素的大小。 LFWCrop中的裁切面表现出真实的条件,包括未对准,缩放比例变化,面内和面外旋转。图5中展示了一些样本图像。实验中,我们选择个人图像数量在20-100之间的人物作为子数据集,其中包括57个类共1883张图像。对于每个人,我们随机选择90%的图像用于训练,其余用于测试。我们重复这个过程10次。


表5和表6分别列出了COIL20数据集、PIE和LFWCrop数据集上的平均识别率和标准偏差。
图像重建实验
在AR数据集上分别用Euler SRC和SRC做图像重建的实验,配置和前面一样。可以看到Euler SRC重建结果残差图中有较清晰的眼镜或围巾图,说明Euler SRC能有效地去除遮挡,这表明图像重建方面Euler SRC优于SRC。

结论
本文呈现了一个称为Euler SRC的图像分类算法。不同于核SRC,Euler SRC显式将图像映射到欧拉空间中且保持维度不增,所以它很容易技术落地。本文提供了寻找精确稀疏表示的算法,能够最优化目标函数。在数据集AR、COIL20、PIE和LFWCrop上的实验证实了我们方法的优越性。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号