岭回归学习记录
引言
解释变量直接存在严重的多重共线性时,用普通的最小二乘法估计模型参数,往往参数估计方差太大,效果很不理想。岭回归是一种改进的最小二乘回归,它通过给 \(X'X\) 加一个正常数矩阵 \(kI(k>0)\) 以偏离奇异,从而使模型稳定。本文先介绍多重共线性的起因及造成的后果,随后讲解岭回归,说明其是如何解决这问题的。笔者水平有限,恐有偏颇之处,恳切希望读者批评指正。
多重共线性
多元线性回归模型有一个基本假设,就是要求设计矩阵 \(X\) 的秩 \(rank(X)=p+1\),即要求 \(X\) 中的列向量之间线性无关。如果存在一组不全为零的数 \(c_0, c_1, \cdots, c_p\) 使得
则自变量 \(x_1, x_2, \cdots, x_p\) 之间存在完全多重共线性。然而在实际问题中这种情形不常见,更多的是上式近似成立的情形,即存在一组不全为零的数 \(c_0, c_1, \cdots, c_p\) 使得
这时称 \(x_1, x_2, \cdots, x_p\) 之间存在多重共线性,也成为复共线性。多重共线性在统计回归中普遍存在,对问题的解具有非常恶劣的影响,下面将对其进行详细介绍。
产生的背景和原因
解释变量之间完全不相关的情形是非常少见的,尤其是在研究某个经济问题时。直觉上,特征数越多模型表征能力就越强,因此,在不明确具体含义的情况下,大多数时候会采集尽可能多的特征进行建模。随着特征数的增多,这些特征之间很难保持线性无关。当它们之间的相关性较弱时,我们一般就认为符合多元线性回归模型设计矩阵的要求;否则,就认为其违背了多元回归模型的基本假设。
当所研究的问题涉及时间序列资料时,由于经济变量往往随着时间存在共同的变化趋势,它们之间很容易出现共线性。例如,我国经济增长势态很好,经济增长对各种经济现象都产生了影响,使得多种经济指标互相密切关联。比如要研究我国居民消费状况,影响居民消费的因素有很多,一般有职工平均工资、农民平均收入、银行利率、全国零售物价指数、国债利率、货币发行量、储蓄额等,这些因素显然即对居民消费产生了重要影响,彼此之间又有很强的相关性。
在研究社会经济问题时,鉴于问题本身的复杂性,设计的因素往往很多。在建立回归模型时,由于研究者认知水平的局限性,很难在众多因素中找到一组互不相关又对因变量有显著影响的变量,不可避免地会出现所选自变量相关的情形。下面将介绍这会造成怎样的问题,以及如何对其进行处理。
多重共线性对模型的影响
先举一个简单的例子。假设有如下自变量(这里没有常数列,所以为 2 列,设计矩阵应包含 3 列)和因变量
显然 \(X\) 的两列存在相关关系,我们采用sklearn库进行线性回归。
import numpy as np
from sklearn.linear_model import LinearRegression
a = np.array([i for i in range(1,6,1)])
b = a * 2
x = np.vstack((a, b))
x = x.T
y = a * 4
y = y.T
model = LinearRegression()
model.fit(x, y)
print(model.coef_)
结果输出为[0.8 1.6]。但其实只要回归系数满足 \(\beta_1 + 2*\beta_2 = 4\),对于给定的输入 \(x\) ,得出的结果总是相同的。当 \(\beta_1 = \pm 1\) 显然存在相应的 \(\beta_2\) 满足前面的等式。问题来了!!!对于给定的问题, \(Y\) 与 \(X_1\) 的相关关系肯定是确定的,怎么可以既具有正相关关系又具有负相关关系!可是为什么会出现这种现象呢?下面将从数学原理的角度对其进行解释。
设计矩阵 \(X\) 的秩 \(rank(X)<p+1\),此时 \(|X'X|=0\),方程解不唯一,回归参数的最小二乘表达式 \(\hat{\beta}=(X'X)^{-1}X'y\) 不成立。
实际问题中,更多情况是近似共线性的情形。此时设计矩阵 \(X\) 的秩 \(rank(X)=p+1\) 虽然成立,但是 \(|X'X|\approx 0\),\((X'X)^{-1}\) 的对角线元素很大,\(\hat {\beta}\) 的方差阵 \(D(\hat {\beta})={\sigma}^2 (X'X)^{-1}\) 的对角线元素很大,而 \(D(\hat {\beta})\) 的对角线元素即 \(var(\hat {\beta_0}),var(\hat {\beta_1}),\cdots,var(\hat {\beta_p})\),因而 \(\beta_0,\beta_1,\cdots,\beta_p\) 的估计精度很低。即使普通最小二乘估计能得到回归系数 \(\beta\) 的无偏估计,但其估计偏差太大,不能正确判断解释变量对被解释变量的影响程度,甚至导致估计量的经济意义无法解释。
疑问:上面说到变量具有多重共线性时,有 \(|X'X|\approx 0\),这里暂时没搞明白,看下面这个例子。
import numpy as np
x = np.array([[ 1, 2, 1],
[ 1, 2, 2],
[ 1, 3, 3],
[ 1, 4, 4],
[ 1, 5, 5],
[ 1, 6, 6],
[ 1, 7, 7],
[ 1, 8, 8],
[ 1, 9, 9],
[ 1, 10, 10]])
print(np.linalg.det(np.dot(x.T, x)))
\(X\) 的第二列和第三列几乎一样,即存在多重共线性问题,但输出为 540.000000000016,看上去一点都不接近 \(0\) 哇!
岭回归的定义及性质
岭回归的定义
针对出现多重共线性时,普通最小二乘法效果变差的问题,霍尔(A. E. Hoerl)于1962年首先提出了一种改进的最小二乘估计的方法,叫岭估计(ridge estimate)。岭回归(ridge regression, RR)的想法是很自然的。自变量间存在多重共线性时,有 \(|X'X|\approx 0\),我们设想给 \(X'X\) 加一个正常数矩阵 \(kI(k>0)\),那么 \(X'X+kI\) 接近奇异的程度就会比 \(X'X\) 接近奇异的程度小得多。考虑到量纲问题,先对变量进行标准化,方便起见,标准化后的设计矩阵仍然用 \(X\) 表示。\(\beta\) 的岭回归估计定义为:
其中,\(k\) 称为岭参数。
岭回归估计的性质
在本节关于岭回归估计的性质的讨论中,假定 \(\beta\) 的估计式中 因变量观测向量 \(y\) 未经标准化。
性质1 \(\hat {\beta (k)}\) 是 \(\beta\) 的有偏估计。
证明:\(\begin{align*}E[\hat\beta (k)] &= E((X'X+kI)^{-1}X'y)\\ &= (X'X+kI)^{-1}X' E(y) \\ &= (X'X+kI)^{-1}X'X\beta \end{align*}\)
显然只有当 \(k=0\) 时,\(E[\hat\beta (0)]=\beta\);当 \(k\ne 0\) 时,\(\hat\beta (k)\) 是 \(\beta\) 的有偏估计。有偏性是岭回归估计的一个重要特性。
性质2 在认为岭参数 \(k\) 是与 \(y\) 无关的常数时,\(\hat\beta (k)=(X'X+kI)^{-1}X'y\) 是最小二乘估计 \(\hat {\beta}\) 的一个线性变换,是 \(y\) 的线性函数。
这句话和废话一样,因为实际应用中岭参数总是通过数据来确定的,所以 \(k\) 总是依赖于 \(y\) 的。
性质3 对任意 \(k>0\),\(||\hat\beta \ne 0||\),总有 \(||\hat\beta (k)||<||\hat\beta||\)。
这个性质表明 \(\hat\beta (k)\) 可看成由 \(\hat\beta\) 进行某种向原点的压缩。当 \(k\to\infty\) 时,\(\hat\beta (k)\to 0\)。
性质4 以MSE表示估计向量的均方误差,则存在 \(k>0\),使得 \(MSE[\hat\beta (k)]<MSE(\hat\beta)\)。
岭参数k的选择
如何确定 \(k\) 的值,目前在理论上上未得到令人满意的答案。近几十年来,不少统计学者相继提出了许多确定 \(k\) 值的原则和方法,这些方法一般都基于直观考虑,具有一定的应用价值,但目前尚未找到一种公认的方法。
选取 \(k\) 值的一般原则是:
- 各回归系数的岭估计基本稳定。
- 用最小二乘法估计的符号不合理的回归系数,其岭估计的符号变得合理。
- 回归系数没有不合乎经济意义的绝对值。
- 残差平方和增加不太多。
下面介绍几种常见的方法。
岭迹法
当岭参数 k 在 \((0,\infty)\) 内变化时,\(\hat\beta_j (k)\) 是 \(k\) 的函数,在平面坐标系上把函数\(\hat\beta_j (k)\) 描绘出来,画出的曲线称为岭迹。
我们可以根据岭迹图的形状 ,判断最小二乘是否合理,并进行调整。
如在下图中,当 k 取 k_0 时,各回归系数的估计值基本上都能相对稳定。
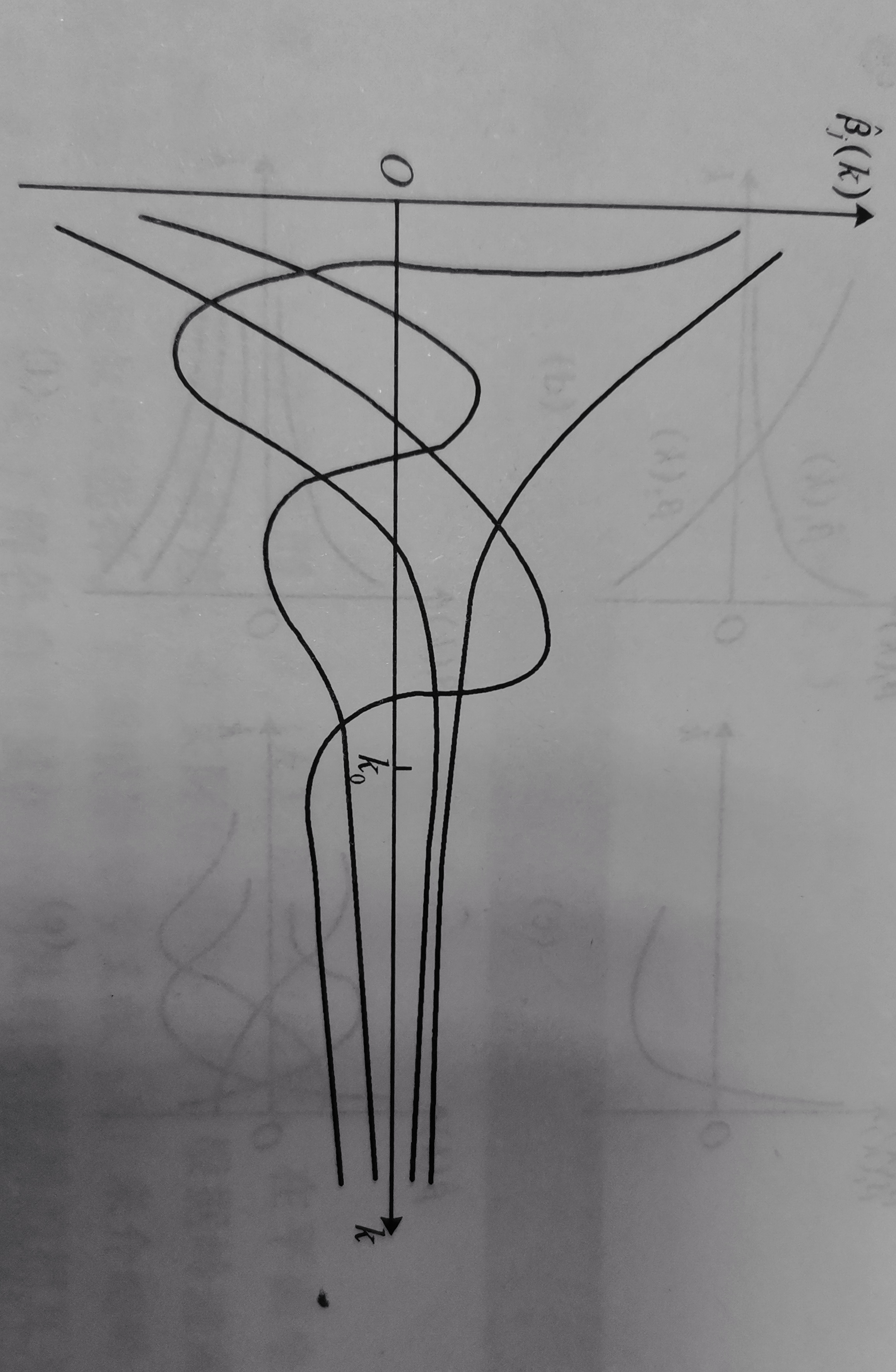
岭迹法缺少令人信服的理论依据,存在一定的主观性。但另一方面,这种主观性正好有助于实现定性分析与定量分析的有机结合。
方差扩大因子法
记
这里 \(X\) 已标准化。称 \(C\) 的主对角线元素 \(c_{jj}\) 为自变量 \(x_j\) 的方差扩大因子。已知,
式中,\(L_{jj}\) 为 \(x_j\) 的离差平方和。由上式可知,用 \(c_{jj}\) 作为衡量自变量 \(x_j\) 的方差扩大程度的因子是恰如其分的。一般当 \(c_{jj}>10\) 时,模型就有严重的多重共线性。计算岭估计 \(\hat\beta (k)\) 的协方差阵,得
式中,矩阵 \(c(k)=(X'X+kI)^{-1}X' X(X'X+kI)^{-1}\),其对角元素 \(c_{jj}(k)\) 为岭估计的方差扩大因子。k 越大, \(c_{jj}(k)\) 越小,应用方差扩大因子法选择 k 的经验做法是:选择 k 使所有方法扩大因子 \(c_{jj}(k) \le 10\) 时,所对应的 k 值的岭估计 \(\hat\beta (k)\) 就会相对稳定。
由残差平方和确定 k 值
岭估计在减小均方误差的同时增大了残差平方和,我们希望将岭回归的残差平方和 SSE(k) 的增加幅度控制在一定的限度以内,从而可以给定一个大于 1 的 c 值,要求
寻找使上式成立的最大的 k 值。
总结
本文先介绍了多重共线性,多重共线性是指存在一组不全为零的常数使得其与自变量线性组合起来近似等于零。多重共线性导致回归系数的方差非常大,尽管仍是无偏估计,但过大的方差通常会导致结果与实际情况不符。随后介绍了岭回归,它是一种改进的最小二乘回归,通过给 \(X'X\) 加一个正常数矩阵 \(kI(k>0)\) 以偏离奇异,从而使模型稳定。最后介绍了岭回归的性质以及参数 \(k\) 的选择。本文数学公式较粗略,详请见参考教材。终。
参考
[1] 何晓群,刘文卿. 应用线性回归. 5版. 北京:中国人民大学出版社,2019.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号