A*寻路算法入门(二)
大熊猫猪·侯佩原创或翻译作品.欢迎转载,转载请注明出处.
如果觉得写的不好请告诉我,如果觉得不错请多多支持点赞.谢谢! hopy ;)
免责申明:本博客提供的所有翻译文章原稿均来自互联网,仅供学习交流之用,请勿进行商业用途。同时,转载时不要移除本申明。如产生任何纠纷,均与本博客所有人、发表该翻译稿之人无任何关系。谢谢合作!
关于A*算法
现在你该知道如何计算每一个方块的分值了(我们将称之为F,它等于G+H),让我们看看A*算法是如何工作的.
这只猫咪将用以下重复的步骤来找到最短路径:
- 从开发列表中取得分值最小的方块,我们称之为方块S.
- 将方块S从开发列表中删除,并且添加到闭合列表中.
- 对于方块S的每一个可到达的邻居方块T:
A.如果T在闭合列表中:忽略它.
B.如果T不在开发列表中:把它添加进来并计算它的分值.
C.如果T已经存在于开放列表中:检查其F值是否比我们使用当前生成的路径要小.如果是,更新它的分值和它父方块.
如果你有点混乱也不用担心 — 我们将用一个例子一步步的像你展示它是如何工作的! :]
猫咪的路径
让我们通过一个例子看看这只懒猫咪是如何找到骨头的.
在下面的图示中,我已经将对应的值列出来了(F = G + H):
- F(方块的分值):左上角
- G(从A点到方块的花费):左下角
- H(从方块到B点的估计花费):右下角
同样,箭头显示出到达该方块的移动方向(指向其父方块.猫猪注).
最终,对于每一步来说,红色方块指示闭合列表,绿色方块指示开发列表.
OK,让我们开始吧!
步骤1
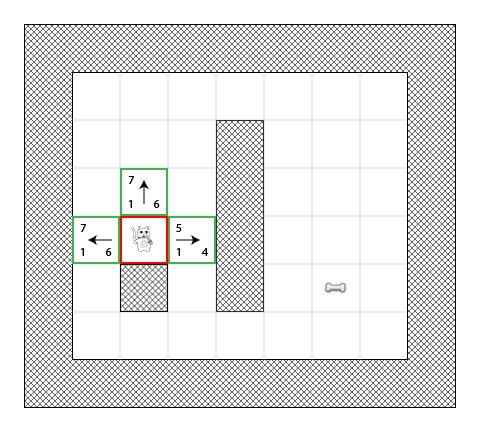
在第一步中,这只猫咪确定其起始位置(点A)的可到的达邻居方块,计算他们的F分值,然后将它们添加到开放列表中:
你可以看到每一个方块中列出了H值(2个为6,一个为4).我建议根据”街区距离”算法自己计算一下,确保你理解这部分是如何工作的.
同样要注意的是F值(左上角)正好是G+H的和(左下角和右下角).
步骤2
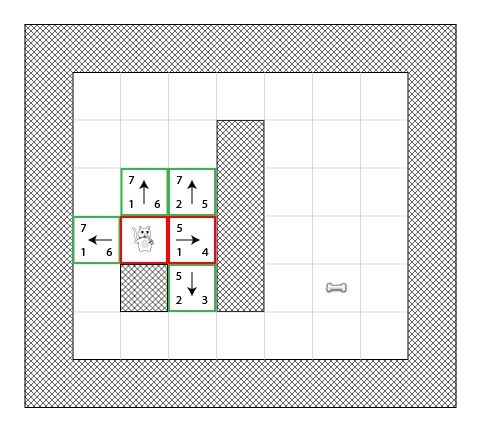
接下来,猫咪选择最小分值的方块,将其添加到闭合列表中去,并且获得他的邻居方块.
所以你将看到最小分值方块的F值为4,我们试图将所有它的邻居瓦块添加到开发列表中(并且计算它们的分值),除非它不能被添加(因为它已经在闭合列表中了)或者它是不可到达的(比如墙壁).
注意这里有2个新的瓦块被添加到开放列表中,G值被加1,因为从起始位置到它们有2个瓦块的距离.你可能想去用”街区距离”算法计算一下以确保你懂了了这些新添加瓦块的H值是如何计算的.
步骤3
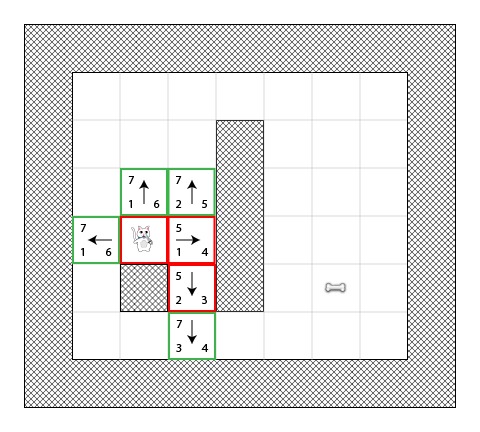
我们再一次选择最小F值(5)的瓦块去继续迭代:
这时,只有一个可能的瓦块被添加到开放列表中,因为一个瓦块已经存在于闭合列表,两个瓦块是墙壁.
步骤4
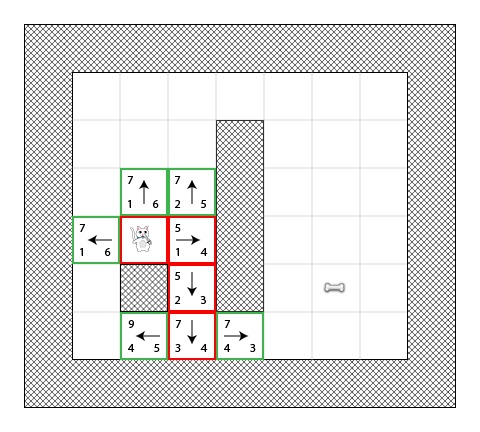
现在我们遇到了一个有趣的情况.正如你在前一张图中看到的,这里有4个方块,它们的F值都是相同的7 — 我们该怎么办呢?!
这里有很多种解决方案可以使用,但是一个简单(也是快速的)的方法是保持跟随最近被添加到开放列表中的瓦块.所以我们从最近的瓦块继续:
这次有2快瓦块是邻接且可到达的,我们像往常那样计算它们的分值.
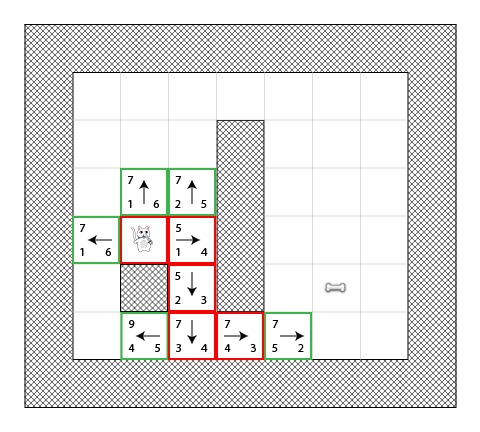
步骤5
我们再一次面临选择最小分值的(7)瓦块,同样选择最近添加的瓦块:
只有1个可能的瓦块被添加.我们离终点越来越近了!
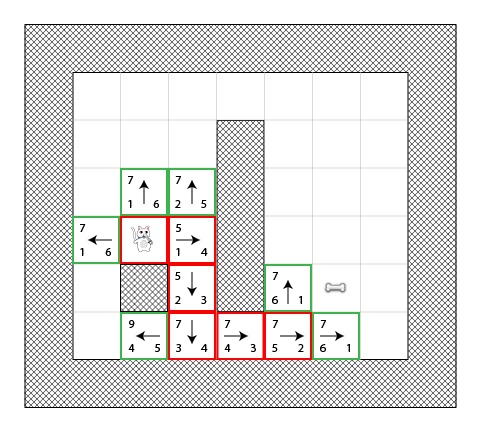
步骤6
你现在已经有经验了!我打赌你可以像下图那样猜出接下里的步骤:
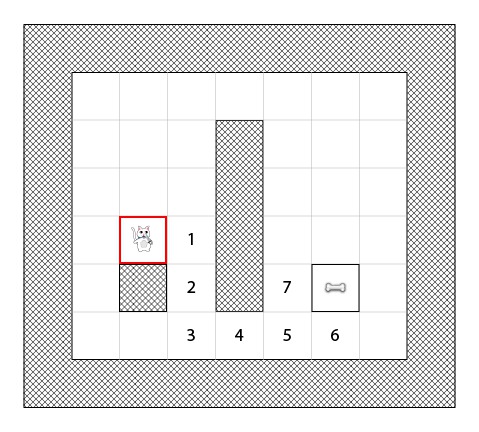
我们几乎完成了,但是这次你可以看到,这里实际我们可以从2条到骨头的最短路径中选择:
在我们的例子中有2条不同的最短路径:
- 1-2-3-4-5-6
- 1-2-3-4-5-7
我们选择哪条无所谓,由后面实际的实现代码来决定.
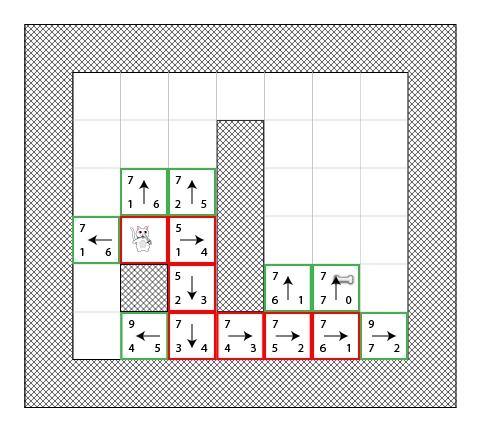
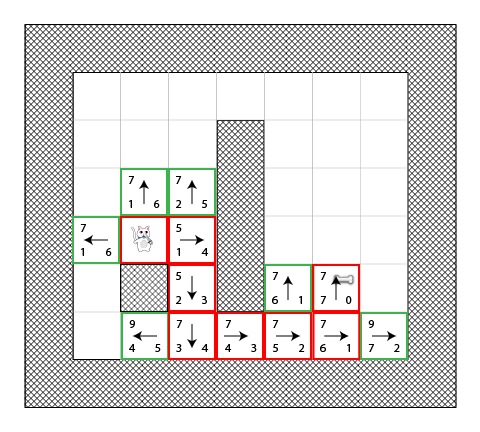
步骤7
让我们再一次枚举一遍这些方块:
Aha,骨头现在在开放列表中了!
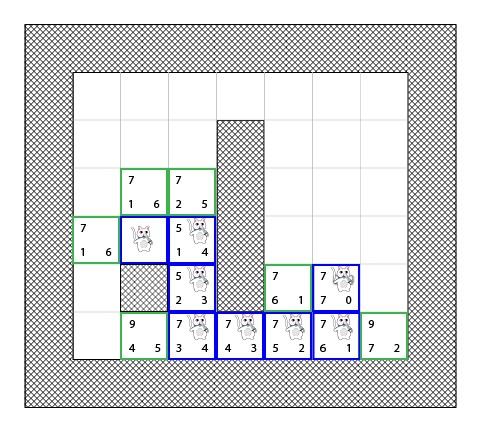
步骤8
此时目的方块在开放列表中,算法将其添加到闭合列表中去:
然后算法要做的只是回退去计算出最终的路径!
一只没有远见的猫咪
在上面的例子中,我们看到猫咪在选择最短路径的时候,它总是选择最好的方块(在未来最短路径中的一块) — 就像他它是一只有远见的猫咪一样!
但是如果这只猫咪不总是头脑清楚的去选择第一个添加到列表中的方块时会发生什么呢?
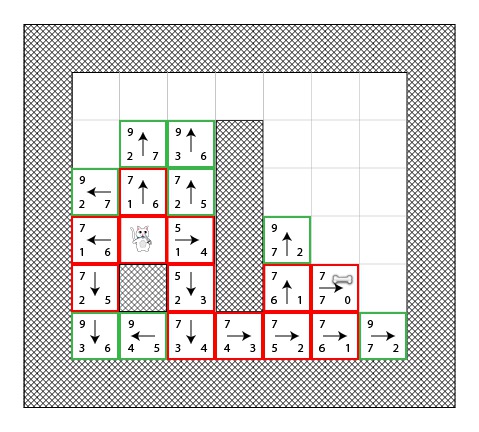
这里有一张示意图显示了这些被用在该处理过程中的方块.你将看到猫咪会尝试更多的方块,但是它仍然能找到一条最短的路径(不一定和前面相同,但是等效的):
上图中红色方块并不表示最短路径,它仅表示在某些点上选择的”S”方块.
我建议你检查上图并且视图跟随遍历它.这次,你将发现无论怎样”最坏的”的路径被选择,在最后你仍然可以得到一条最短的路径!
所以你可以看到跟随”错误”的方块也没有关系,在最终你仍然可以得到最短路径,即使你会经历更多次的迭代.
在我们的实现中,我们将按以下算法将方块添加到开放列表中去:
- 邻居方块将按以下顺序返回:上/左/下/右.
- 一个具有相同分值的方块将被添加到开放列表中所有相同分值相同方块的最后面(所以第一个添加的将第一个被猫咪取得).
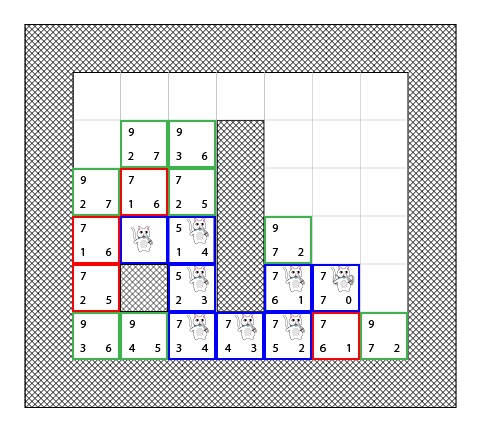
这里是一张回溯的示意图:
最短路径通过开始从目的地回退到其父方块来建立起来(比如:在目的地我们可以看到箭头指向右侧,所以该方块的父方块在它的左侧).
最终,我们可以通过下面的伪代码来合成猫咪的处理.它被写为Objective-C,但是你可以用任何语言实现:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
你有没有小激动想要实现一下?!在下一篇课程中,我们将完全实现它!
接下来呢?
恭喜,你现在了解了基本的A*寻路算法!如果你想要从这里学到更多内容,我推荐你阅读 Amit’s A* Pages.
在本系列的下一篇课程中,我们将在一个简单的Cocos2D地图游戏中实现A*算法!(之前猫猪写过的 Cocos2D将v1.0的tileMap游戏转换到v3.4中一例系列博文即是前奏,大家可以先看一下 ;)
与此同时,如果你有关于A*算法的任何问题,请加入下面的讨论中来!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号