codeforces 1294 E 思维

还以为是把1，4，7，10，13搞成1，4，7，10，13，1，4，7，10，13，然后用kmp的思想,👎

思路：给你一个n*m的矩阵，你可以进行若干次操作

　　op1：让一列往上移动一位。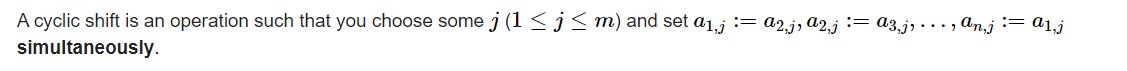

 

 　　op2：让一个位置的数改变。

思路:每列单独进行思考。对于第一列，若n为5，m为3。给你n数，问你进行最少多少次操作可以使得其成为1，4，7，10，13。

　　用相对位置解决。（因为n和m最大为2e5，所以二维数组用不了了，用了vector下标问题就有差别了，下面的数组都是从0-n-1.)

　　比如，在这一列存在一个数7，则找到7应该存在的位置，计算两个位置的差step，相对位置即为step，查看这些点存在最多的step是多少vis[step]，如果是移动step步，

则要所有点匹配的值为 n-vis[i] + i。瞎搞即可。

　　

#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <string>
#include <map>
#include <iomanip>
#include <algorithm>
#include <queue>
#include <stack>
#include <set>
#include <vector> 
// #include <bits/stdc++.h>
#define fastio ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define sp ' '
#define endl '\n'
#define inf  0x3f3f3f3f;
#define FOR(i,a,b) for( int i = a;i <= b;++i)
#define bug cout<<"--------------"<<endl
#define P pair<int, int>
#define fi first
#define se second
#define pb(x) push_back(x)
#define ppb() pop_back()
#define mp(a,b) make_pair(a,b)
#define ms(v,x) memset(v,x,sizeof(v))
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define repd(i,a,b) for(int i=a;i>=b;i--)
#define sca3(a,b,c) scanf("%d %d %d",&(a),&(b),&(c))
#define sca2(a,b) scanf("%d %d",&(a),&(b))
#define sca(a) scanf("%d",&(a));
#define sca3ll(a,b,c) scanf("%lld %lld %lld",&(a),&(b),&(c))
#define sca2ll(a,b) scanf("%lld %lld",&(a),&(b))
#define scall(a) scanf("%lld",&(a));


using namespace std;
typedef long long ll;
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
ll powmod(ll a, ll b, ll mod){ll sum = 1;while (b) {if (b & 1) {sum = (sum * a) % mod;b--;}b /= 2;a = a * a % mod;}return sum;}

const double Pi = acos(-1.0);
const double epsilon = Pi/180.0;
const int maxn = 2e5+10;
int n,m;
int vis[maxn];    
vector<int>a[maxn];
int main()
{

    cin>>n>>m;
    rep(i,0,n-1){
        rep(j,0,m-1){
            int tmp;
            cin>>tmp;
            a[j].pb(tmp);
        }
    }
    int ans = 0;
    for(int j=0;j<=m-1;++j){
        rep(i,0,n-1){
            vis[i] = 0;
        }
        for(int i=0;i<a[j].size();++i){
            int x = a[j][i];
            if((x-(j+1))%m != 0 || x > n*m) {
                //nub++;
                continue;
            }
            int pos = (x-(j+1))/m;
            int step = (i-pos+n)%n;
            vis[step]++;
        }
        int sum = n;
        rep(i,0,n-1){
            int cnt = n-vis[i] + i;
            sum = min(sum,cnt);
        }
        ans += sum;
    }

    cout<<ans<<endl;

}