Codeforces 1312D 组合数学

Cnub

 

 

 

 题意：

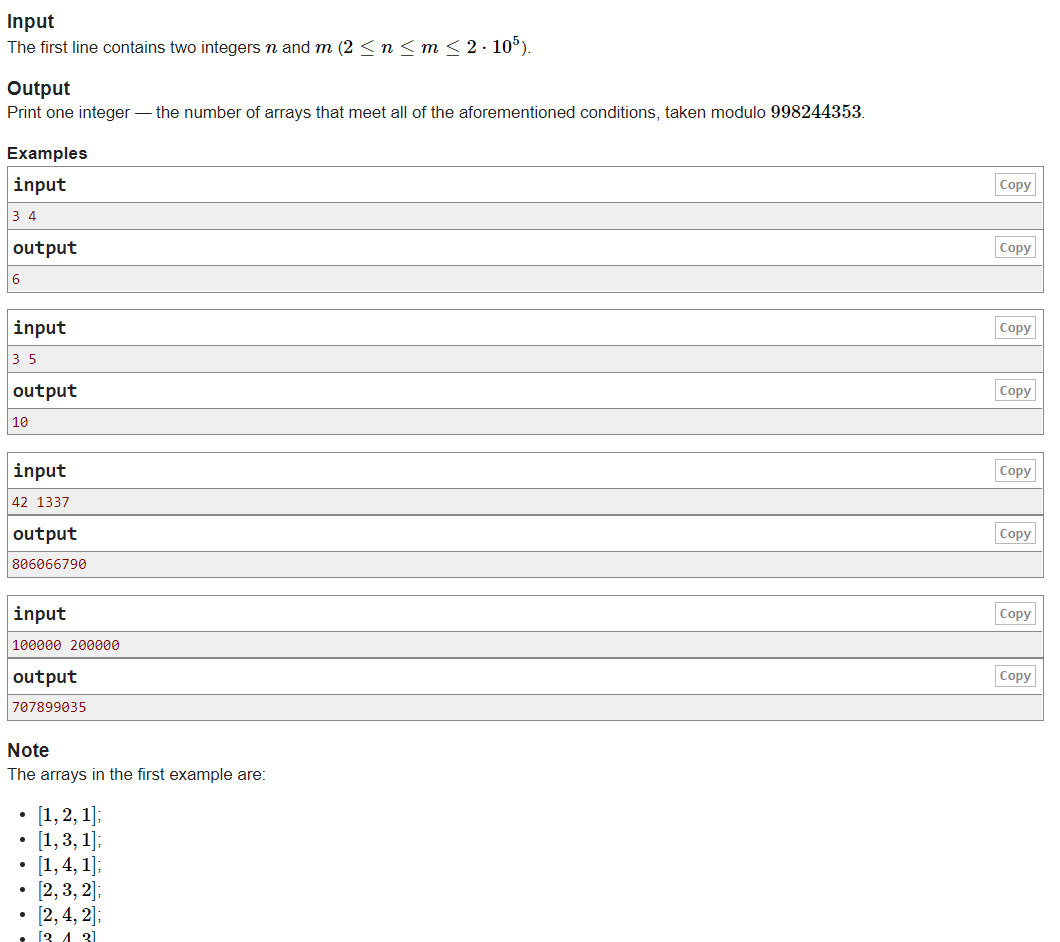
给你nn和mm，问满足以下条件的数列的个数：

• 数列长度为nn
• 数列值域范围为[1,m][1,m]
• 数列有且仅有一对相等的数
• 数列是单峰数列（先严格递增后严格递减，严格递增或严格递减）

思路：数列有且仅有一对相等的数，所以每次要从m个数中挑n-1个数，既是组合数C^n-1m。当找到n-1个数的时候，要满足先严格递增后严格递减，严格递增或严格递减，所以最大值要确定在中间，我们只需要确定最大值两边的数即可，因为要存在一对相等的数且满足单峰数列，要选择的这个存在两次的数不能是这个最大值，要从n-2中选择。当选择出来了出现两次的数的时候，把这个数分别放在最大值的两边，接下来只需要计算剩余n-3个数分配在两边所出现的可能性，既是2^n-2。

答案即为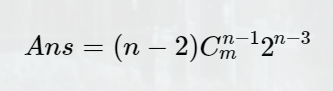

 

 

#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <string>
#include <map>
#include <iomanip>
#include <algorithm>
#include <queue>
#include <stack>
#include <set>
#include <vector>
//const int maxn = 1e5+5;
#define ll long long
#define inf  0x3f3f3f3f
#define FOR(i,a,b) for( int i = a;i <= b;++i)
#define bug cout<<"--------------"<<endl
 
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
 
using namespace std;
 const ll mod = 998244353 ;
ll pow_(ll a,ll b)
{
    ll res = 1;
    while(b>0)
    {
        if(b & 1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}
 
ll Cnub(ll n,ll m)
{
    ll res = 1;
    ll tmp = 1;
    for(int i = 1; i <= n; i++) res = res * i % mod;
    for(int i = 1; i <= m; i++) tmp = tmp * i % mod;
    for(int i = 1; i <= n-m; i++) tmp = tmp * i % mod;
    return res * pow_(tmp, mod-2) % mod;
}
 
int main()
{
    ll n,m,a,b,c;
    cin>>n>>m;
    if(n == 2)
    {
        cout<<0<<endl;
        return 0;
    }
    ll ans = ((Cnub(m,n-1) * (n-2) % mod) % mod * pow_(2,n-3)%mod) % mod;
    cout<<ans<<endl;
}