Codeforces 1284C 组合数学

no

 

 

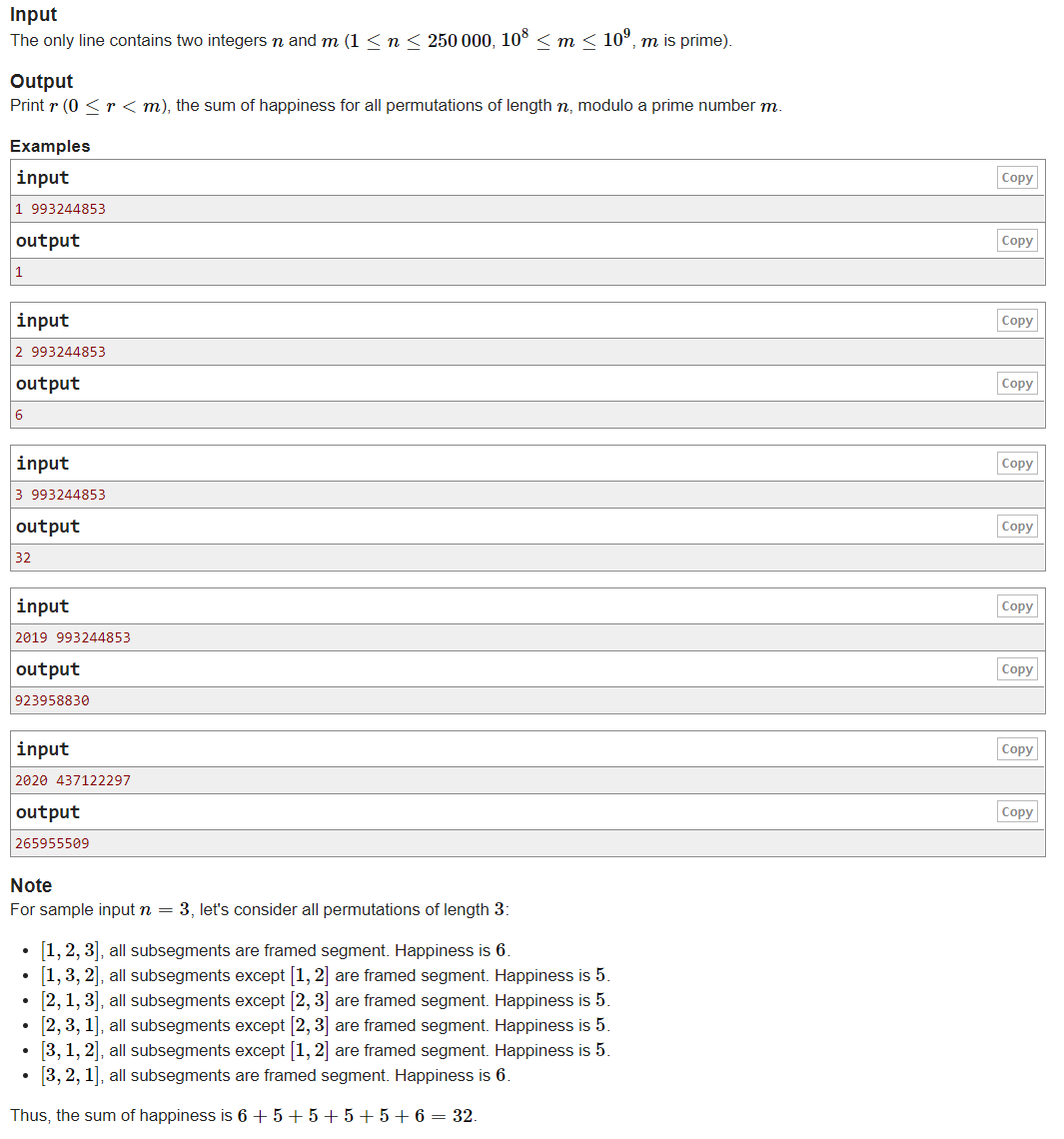
 题意：定义一个framed segment，在区间[l,r]中，max值-min值 = r - l。求有1-n 组成的序列中，所有framed segment的个数%m

思路：组合数学推一个结论。例如假设1到n组成的序列中，求长度为k的framed segment，那么其一段序列的最大值 - 最小值 = k，例如n = 5,k = 3，这些framed segment 必定是 1 2 3 或者2 3 4 或者 3 4 5，可以观测到其长度为k的framed segment必定是连续的，可以把他们单独算一个整体，这样序列总体长度变为n - k + 1，内部长度为k，内部组合种类就是k!个，总体组合种类就是(n-k+1)！，长度为k的framed segment种类又是（123，234，345）n - k + 1种，所以长度为k的framed segment 最终答案就是(n-k+1)*(n-k+1)!*k!，预处理一下阶乘即可。

倘若n=3，k=2。ans += (n-k+1)*(n-k+1)!*k! = 2 * 2 * 2, 第一个2代表的有两种长度为2 的组合（1，2）和（2，3）。第二个2代表假如把（1，2）看成一个整体A，有两种方式（A，3）和（3，A），注意不是这个整体(A,3)所作出的贡献（整体做出的贡献是在k=n），而是这个组合（A，3）中 的A做出的贡献。第三个2代表k！，既是（1，2）的全排列。

 

#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <string>
#include <map>
#include <iomanip>
#include <algorithm>
#include <queue>
#include <stack>
#include <set>
#include <vector>
//const int maxn = 1e5+5;
#define ll long long
#define inf  0x3f3f3f3f
#define FOR(i,a,b) for( int i = a;i <= b;++i)
#define bug cout<<"--------------"<<endl
 
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
 
using namespace std;
const int maxn = 250000;
ll dp[maxn+5];
int main()
{
    ll n,mod;
    cin>>n>>mod;
    ll temp = 1;
    for(ll i = 1;i <= n; ++i)
    {
        temp = ((temp % mod) * (i % mod)) % mod;
        dp[i] = temp;
    }
    ll ans = 0;
    for(ll i = 1;i <= n; ++i)
    {
        ans += ((dp[i]%mod * (n-i+1)%mod)%mod * dp[n-i+1]%mod)%mod;
        ans %= mod;
    }
    cout<<ans<<endl;
}