基础莫队算法
莫队算法(Mo's Algorithm)
前置知识
最好是会一点线段树,不会也没有关系
正文
我们都知道,维护区间信息的时候通常会用到各种线段树,因为其本身具有的性质可以在很快的速度内完成各种操作。但是这是基于我们上推(pushup)和下推(pushdown)这两种操作可以在O(1)的时间内完成的基础。如果这两个操作本身需要的时间不是常数级别的化我们可能需要考虑其他的方法。莫队算法可以有效地解决一部分这样的问题。更加精确地来讲,普通莫队算法可以解决的问题有以下两种特征:
- 只有查找,没有修改
- 从区间\([ l , r]\)拓展到区间\([ l\pm1,r\pm1]\)的时间消耗是常数级别的
当然莫队算法还有很多其他的变种,类似于树上莫队,代修莫队等等。这里我们只介绍最简单的基础莫队。
简单来讲,莫队算法的思想就是用特殊的顺序对询问进行排序使得程序运行时间加快。
打个比方,我们现在要维护区间和,并且假设大家都没学过前缀和,树状数组和线段树,那么我们能想道的最朴素的算法就是对于每一个询问都老老实实地从 l 遍历到 r 。但是我们发现了一个问题,对于两组询问, \([l_1,r_1]\)和\([l_2,r_2]\)来讲,如果出现了下图的情况:
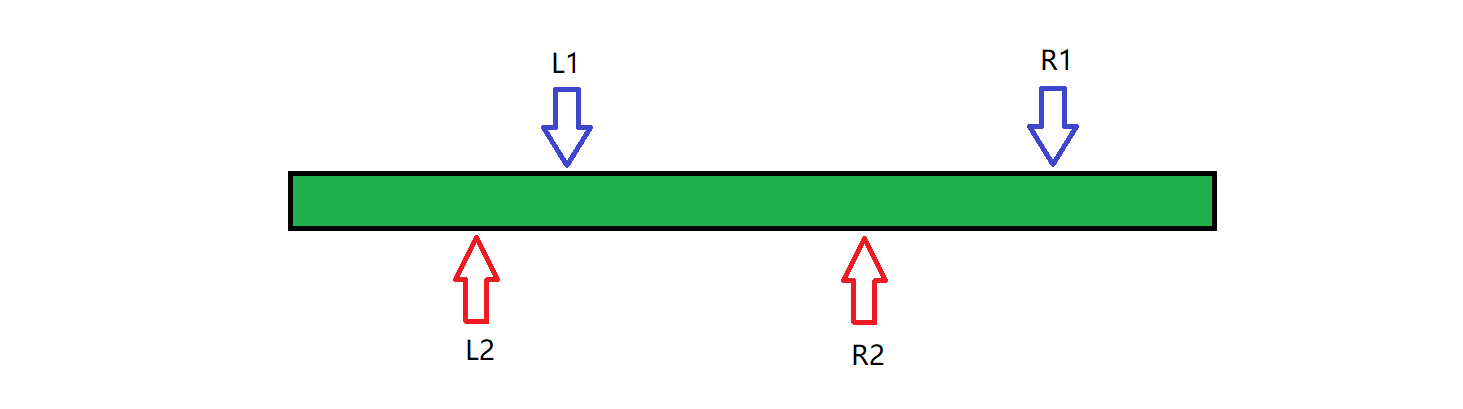
我们是没必要在第二个询问的时候重新遍历的,因为区间 \([l_1,r_2]\)的答案实际上已经包含在了\([l_1,r_]\),也就是第一次询问里面了,并且从\(l_1\)扩展到\(l_2\),\(r_1\)扩展到\(r_2\)的时间消耗可能比较低(因为从位置\(i\)扩展答案到\(i\pm1\)的位置的时间消耗是O(1)的)。这就是莫队算法的思想,还是比较简单的。
那么可能有人要问了,如果我们的查询区间是类似于: \([1,2]\),\([n-1,n]\),\([1,3]\),\([n-2,n]\)这样的,相邻询问跨度很大并且没有交集的情况该怎么半呢?这里我们可以对询问进行排序。可以把每一个和询问抽象成平面上面的两个点,那么询问\([l_1,r_1]\)到\([l_2,r_2]\)的时间消耗就是\(ABS(l_1-l_2)+ABS(r_1-r_1)\),也就是这两个点之间的曼哈顿距离。那么我们对询问的排序也就很明显了,就是求这幅图的最小曼哈顿距离生成树。
但是这么写的化码量实在是有一些大(计算几何题的代码复杂程度大家肯定也是有目共睹的),那么我们能不能找到一个不错的替代品呢?
分块,yyds
我们简单地对区间进行分块,然后对于左区间在同一块内的群问按照右区间从小到大排序,否则就按照左区间进行排序,这样的化就可以有效地加快程序运行速度。
例题: 小B的询问
简单来说就是要你维护每一个数字在区间\([l,r]\)内部出现次数的平方和。
用线段树是会T的,但是我们新加一个数到答案里面的时间是常数的,所以我们可以考虑用莫队
首先我们需要把询问给存储起来,最好还是另外存一个k来表示第k个询问,因为最后输出的时候还是会检查你的顺序的
struct Q{
int l,r,k;
}q[maxn];
然后就正常读入啊什么的,顺便分个块
scanf("%d %d %d",&n,&m,&k);
int siz=n/sqrt(m*2/3);//似乎说是这么分会快一点
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
pos[i]=i/siz;
}
for(int i=1;i<=m;i++){
scanf("%d %d",&q[i].l,&q[i].r);
q[i].k=i;
}
接着写一下排序的cmp函数:
bool cmp(Q a,Q b){
if(pos[a.l]==pos[b.l]) return a.r<b.r;
return pos[a.l]<pos[b.l];
}
在后面就是莫队的基本操作了:
sort(q+1,q+m+1,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++){
while(q[i].l<l) add(--l);
while(q[i].r<r) sub(r--);
while(q[i].l>l) sub(l++);
while(q[i].r>r) add(++r);
ans[q[i].k]=rsl;
}
这里的add函数和sub函数就是计算新增加/减少的一个数对答案的贡献的函数,后面一定要记得按照每一个询问的k值来村答案
void add(int n){
cnt[a[n]]+=1;
rsl+=(cnt[a[n]])*(cnt[a[n]])-(cnt[a[n]]-1)*(cnt[a[n]]-1);
}
void sub(int n){
cnt[a[n]]-=1;
rsl-=(cnt[a[n]]+1)*(cnt[a[n]]+1)-(cnt[a[n]])*(cnt[a[n]]);
}
最后再输出一下就好了
AC代码全放送:
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5;
struct Q{
int l,r,k;
}q[maxn];
int a[maxn],cnt[maxn],pos[maxn],n,m,k,ans[maxn],rsl;
bool cmp(Q a,Q b){
if(pos[a.l]==pos[b.l]) return a.r<b.r;
return pos[a.l]<pos[b.l];
}
void add(int n){
cnt[a[n]]+=1;
rsl+=(cnt[a[n]])*(cnt[a[n]])-(cnt[a[n]]-1)*(cnt[a[n]]-1);
}
void sub(int n){
cnt[a[n]]-=1;
rsl-=(cnt[a[n]]+1)*(cnt[a[n]]+1)-(cnt[a[n]])*(cnt[a[n]]);
}
int main(void){
scanf("%d %d %d",&n,&m,&k);
int siz=n/sqrt(m*2/3);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
pos[i]=i/siz;
}
for(int i=1;i<=m;i++){
scanf("%d %d",&q[i].l,&q[i].r);
q[i].k=i;
}
sort(q+1,q+m+1,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++){
while(q[i].l<l) add(--l);
while(q[i].r<r) sub(r--);
while(q[i].l>l) sub(l++);
while(q[i].r>r) add(++r);
ans[q[i].k]=rsl;
}
for(int i=1;i<=m;i++){
printf("%d\n",ans[i]);
}
}
额外的(常数)优化
这里我们还可以用一个小技巧,就是如果两个\(l\)所在的块是奇数块的化\(r\)就要从小到大排序,如果是偶数块的化就从大到小。这样的化对于在同一个块内的询问我们就可以在回来的之后顺便计算下一次询问的值了。



