tarjan算法求scc & 缩点
前置知识
图的遍历(dfs)
强连通&强连通分量
对于有向图G中的任意两个顶点u和v存在u->v的一条路径,同时也存在v->u的路径,我们则称这两个顶点强连通。以此类推,强连通分量就是某一个分量内各个顶点之间互相连通。
简单来说,就是有向图内的一个分量,其中的任意两个点之家可以互相到达。
求有向图内部强连通分量的方法大概有2种:tarjan算法,korasaju算法。这里我们只对tarjan算法进行讨论。
tarjan算法
tarjan算法是tarjan神仙提出的基于dfs时间戳和堆栈的算法,这里我们可以先来看一下什么是dfs时间戳
dfs时间戳
dfs时间戳就是dfs的先后顺序,详细来讲,比如我们dfs最先访问到的节点是A,于是A的时间戳就是1,第二个访问到的节点是E,那么E的时间戳就是2,我们用\(dfn[u]\)来表示u节点的时间戳,应该算是比较简单的
算法步骤
首先,除了dfn以外我们还需要一个low数组,这个数组记录了某个点通过图上的边能回溯到的dfn值最小的节点。这句话相信在大多数博客里面都有提到,这里我们来看一个简单的例子:
首先,我们有一个图G:

假设我们从a点出发开始dfs,我们可以画出一个dfs树:

为什么我们画出来的dfs树和原来的图不一样呢?因为我们在dfs的过程中实际上是会忽略某一些连接到已访问节点的边的,这些边我们暂且称之为回边。对于点u来说,\(low[u]\)保存的就是点u通过某一条(或者是几条)回边能到达的dfn值最小的节点(也就是被最先访问的节点)。假设这个dfn值最小的节点是u',我们可以知道,因为u和u'都是在一棵dfs树上的,并且u'可以到达u,同时u可以通过一条或多条回边到达u',也就是说u'->u路径上的任意节点都可以通过这一条回边来互相到达,也就是说他们会形成一个强连通分量。
更加详细的例子
我们有一个新图G:
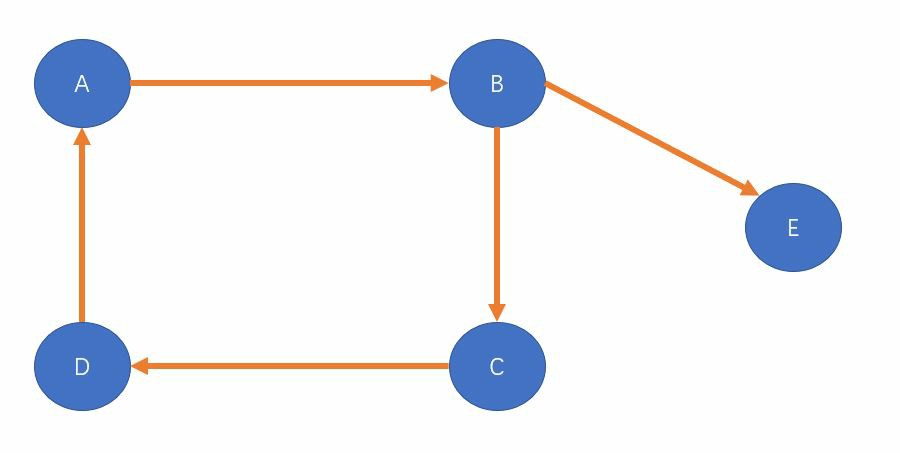
假设我们从A点出发开始dfs,一路跑到D点,那么我们为这个图上的每一个点加上dfn数组和low数组的值(dfn,low),整个图就会长成这个样子:
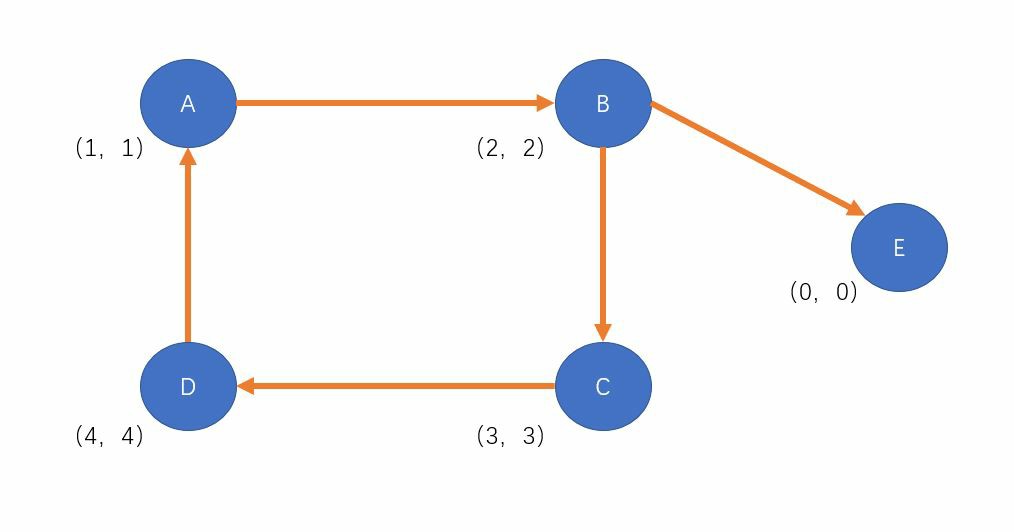
此时我们会遇到一条D->A的回边,也就是说点D能访问到的dfn值最小的节点从点D本身变化到了A点,所以点D的low值就会发生相应的变化,\(low[D]=min(low[D],dfn[A])\)。
紧接着,dfs发生回溯,我们沿着之前的路径逐步更新路径上节点的low值,于是就有\(low[C]=min(low[C],low[D])\),直到更新到某一个dfn值和low值相同的节点。因为这个节点能访问到的最小dfn的节点就是其本身,也就是说这个节点是整个scc最先被访问到的节点。
全部搞完大概会变成这个样子:

我们用一个辅助栈来保存dfs的路径,这样就可以在找到一个强连通分量里面最早被访问到的节点的时候可以输出路径。同时因为dfs访问是一条路走到黑的,所以可以保证栈内在节点u(low[u]==dfn[u])之前的的节点都是属于同一个scc的。
还是上面这幅图,我们顺便把E点给更新了:

跑完E点之后就会发现,E点本身的low就是和dfn相等的,所以此时栈内也只有E这一个节点。
于是上面这个图的scc有以下几个:
[E]
[A,B,C,D]
代码实现
首先我们要发现,在dfs的初期我们每一个节点的low和dfn都是相同的,也就是说有dfn[u]=low[u]=++cnt(cnt为计数变量),并且在回溯的过程中要用后访问节点的low值来更新先访问节点的low值,也就是说有\(low[u]=min(low[u],low[v])\),当访问到某一个在栈中的节点的时候,我们要用这个节点的dfn值来更新其他节点,所以有\(low[u]=min(low[u],dfn[v])\)。
那么我们一个简单的代码就可以写出来了:
void tarjan(int u){
dfn[u]=low[u]=++cnt;
s.push(u);
ins[u]=1;
for(int i=0;i<gpe[u].size();i++){
int v=gpe[u][i].to;
if(!dfn[v]){//如果节点未访问,则访问之
tarjan(v);
low[u]=min(low[u],low[v]);
}else if(ins[v]){//ins是为栈中节点做的一个标记
low[u]=min(low[u],dfn[v]);
}
}
}
当更新完毕之后,我们需要找出一个完整的scc,因为我们提前已经用辅助栈来记录节点了,剩下的工作就只剩下从栈中不停地pop就完事了
if(low[u]==dfn[u]){
ins[u]=0;
scc[u]=++sccn;//sccn是强连通分量的编号
size[sccn]=1;//size记录了强连通分量的大小
//找到某一个low[u]==dfn[u]的节点的时候就要立即处理,因为这个节点也属于一个新的scc
while(s.top()!=u){
scc[s.top()]=sccn;//scc[u]记录了u点属于哪一个scc
ins[s.top()]=0;
size[sccn]+=1;
s.pop();
}
s.pop();
//这里pop掉的就是一开始的那个low[u]==dfn[u]的节点。因为相关信息已经维护完毕,所以这里直接pop也没问题
}
把这两部分结合在一起,就是tarjan求scc的完整代码了:
void tarjan(int u){
dfn[u]=low[u]=++cnt;
s.push(u);
ins[u]=1;
for(int i=0;i<gpe[u].size();i++){
int v=gpe[u][i].to;
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}else if(ins[v]){
low[u]=min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u]){
ins[u]=0;
scc[u]=++sccn;
size[sccn]=1;
printf("%d ",u);
while(s.top()!=u){
scc[s.top()]=sccn;
printf("%d ",s.top());
ins[s.top()]=0;
size[sccn]+=1;
s.pop();
}
s.pop();
printf("\n");
}
return;
}
tarjan与缩点
tarjan算法最有用的地方就是缩点了。缩点,顾名思义,就是把图上的某一块的信息整合成一个点,从而使得后续处理的速度加快(个人的简单总结,可能会有遗漏之类的)。
先来一个模板题吧:
emmm......题目大意就是对于一条边u->v代表了u喜欢v ,然后给出了一个奶牛和奶牛之间的关系网(不要问我为什么是奶牛,这不是usaco题目的传统艺能吗),要你求出这群奶牛之中的明星奶牛。明星奶牛就是那些被所有奶牛所喜欢的奶牛。这里要注意,喜欢是可以传递的,也就是说a->b,b->c,那么a->c。(更多题目细节可以去连接里面看看)
首先最朴素的dfs方法就是对于每一个点来检查喜欢它的节点的数量,但是这样的效率肯定是太低了,所以我们考虑缩点。如果在这个关系网内部存在某一个强连通分量,也就是说这个分量里面的每一个奶牛都是互相喜欢着的,并且任何喜欢这个分量的奶牛都会喜欢到这个分量内部的每一个奶牛,于是我们可以把这个分量当成一个点来看待。
缩点结束之后的新图肯定是一个DAG(有向无环图),又因为缩点本身对题目是没有影响的,所以我们可以基于这个DAG来分析题目,比之前算是简单许多了。
很明显,一个DAG里面只能有一个明星牛(或者是由明星牛组成的SCC),因为当存在两个的时候他们是无法互相喜欢的(如果互相喜欢的话就会被缩成一个点)
答案就很明显了,我们只需要维护每一个SCC的出度(出度为0则证明这就是一个明星),如果存在两个或两个以上的明星则证明这个图里面没有明星。如果只有一个的话我们就在tarjan里面顺手维护每一个scc的大小,最后统计一下输出就完事了
AC代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn=10010;
struct edge{
int to;
edge(int to_){
to=to_;
}
};
vector<edge> gpe[maxn];
int dfn[maxn],low[maxn],ins[maxn],scc[maxn],size[maxn],cnt=0,sccn=0;
stack<int> s;
void tarjan(int u){
dfn[u]=low[u]=++cnt;
s.push(u);
ins[u]=1;
for(int i=0;i<gpe[u].size();i++){
int v=gpe[u][i].to;
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}else if(ins[v]){
low[u]=min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u]){
ins[u]=0;
scc[u]=++sccn;
size[sccn]=1;
while(s.top()!=u){
scc[s.top()]=sccn;
ins[s.top()]=0;
size[sccn]+=1;
s.pop();
}
s.pop();
}
return;
}
int n,m,oud[maxn];
int main(void){
scanf("%d %d",&n,&m);
memset(low,0x3f,sizeof(low));
memset(ins,0,sizeof(ins));
for(int i=1;i<=m;i++){
int u,v;
scanf("%d %d",&u,&v);
gpe[u].push_back(edge(v));
}
for(int i=1;i<=n;i++){
if(!dfn[i]){
cnt=0;
tarjan(i);
}
}
for(int u=1;u<=n;u++){
for(int i=0;i<gpe[u].size();i++){
int v=gpe[u][i].to;
if(scc[u]!=scc[v]) oud[scc[u]]++;
}
}
int cont=0,ans=0;
for(int i=1;i<=sccn;i++){
if(oud[i]==0){
cont++;
ans+=size[i];
}
}
if(cont==1){
printf("%d",ans);
}else{
printf("0");
}
return 0;
}
代码以前写的,略冗长,见谅
题目推荐:



