数据结构——主席树&可持久化数组
前置知识
线段树,离散化
名字的来历

如图所示,因为 黄嘉泰→HJT→某一名president名字的缩写,所以得名主席树
维护什么
在这题里面我们要维护区间第k大
区间第k大,如果我们把单个区间拎出来直接排序的话时间复杂度是O(mnlogn),肯定是会T飞的,所以这种做法可以不不用考虑了
权值线段树
先要了解一下权值线段树
我们知道,普通线段树维护的是序列区间和,也就是说普通线段树是以数列下标来维护的(比如说你要查找sum[l~r]意思是说查找序列的第l个数到第r个数这个区间内的和,本质上是以下标来标示区间的)。权值线段树在这一点上不同,它是以值来标记一段区间的。
打个比方,对于数列:1,1,1,2,3,4,4,5,我们[1,1]的值是3,[2,2]的值是1,[3,3]的是1,[4,4]的值是2,[5,5]的值是1。可以看出,对于某一个区间[l,r],权值线段树维护的是在这个区间范围内的数的个数。应该还是比较好想的
但是,如果数字太大我们就要考虑离散化。
emmm代码就不放了,反正我们的重点也不是这里
可持久化
这里还是提一下可持久化的含义吧。。。。
可持久化分为部分可持久化和完全可持久化
部分可持久化
就是对于历史的所有版本的数据结构都可以询问,但是只能对于最新版的才可以修改
完全可持久化
就是不管是历史还是最新版本的数据结构都可以进行访问和修改
我们在这一题里面的区间第k大,本质上就是把每一次插入数据当成新开了一棵权值线段树(也就是新开了一个版本),然后对于区间[l,r],我们对历史l的线段树和历史r的线段树进行查询
线段树新开n个版本,可能最简单的想法就是给之前的线段树完完整整复制到内存里面去:
但是,单个线段树的空间复杂度是2n(优化一下),对于每一次操作都开的话空间复杂度就会很高,并且完整复制一遍前面的线段树所花费的时间也是很多的,所以我们不能这样直接莽
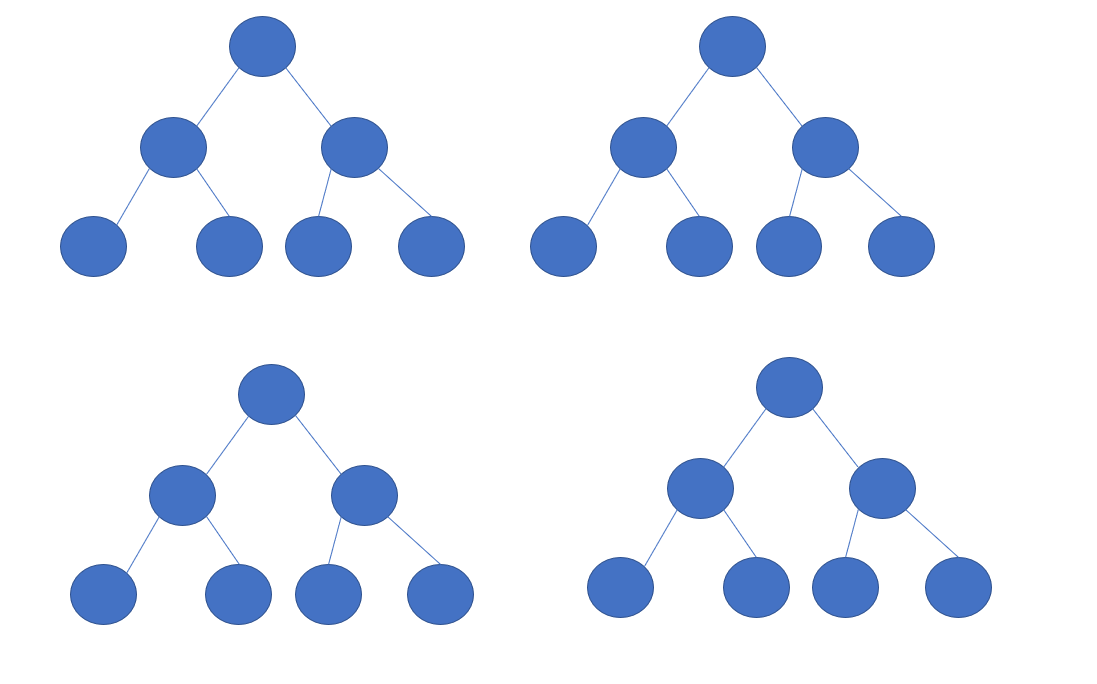
我们可以发现,如果更改线段树上任意一个点,那么受影响的也只有这个点到树根的这一条路径,剩下的部分在更改前后都是一样的,那么我们只用更新这一条路径不就好了吗?我们每一次更新路径,根节点也必定会被更新到,那么我们就单独把这条路径拿出来当作一个新版本,然后把两个版本之间没区别的点都连上:
放个图也许会更加清晰:

蓝色的节点是我们第一个版本的线段树,橙(黄?)色的节点是我们更新的路径
可以看出,不管是从第一个线段树的根还是从第二个线段树的根来看,整棵树都是完整的,所以我们只用去新开一条链就可以了
代码部分
首先,我们需要对输入进行离散化:
for(int i=1;i<=n;i++){
scanf("%d",&arr[i]);
v.push_back(arr[i]);
}
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
然后写一个获取对应值的函数:
int getindex(int val){
return lower_bound(v.begin(),v.end(),val)-v.begin()+1;
}
还是蛮简单的(
接下来就是我们的insert函数了
这里我们观察一下上面那个图的橙色节点,我们可以发现,每个橙色节点和其所对应的蓝色节点之间的区别只有一个儿子的不同,所以我们建立新点的思想就是基于原点的“副本”,然后再更具插入数据来递归地判断到底该改变哪一条边
先给出基本变量的定义:
struct node{
int sum,l,r;
}hjt[maxn*40];
int n,m,root[maxn],cnt=0,arr[maxn];
然后就是insert函数,解释都在注释里面了
void insert(int l,int r,int pre,int &now,int p){
hjt[++cnt]=hjt[pre];//基于副本,所以先复制过来
now=cnt;//更新now
hjt[now].sum++;//插入新点,sum要自增
if(l==r){
return;//遇到根就返回
}
int mid=(l+r)/2;
if(p<=mid) insert(l,mid,hjt[pre].l,hjt[now].l,p);//判断插入的节点到底是该更改那一条边(板子还是很好背的)
else insert(mid+1,r,hjt[pre].r,hjt[now].r,p);
}
这里我们要传入的pre和now分别是上一个版本的树的根节点和我们要插入的节点,当然初始状态下就是新的根节点。因为我们最新版本的树的根都是不同的,所以我们的now要传引用去不断更新。
那么该怎么写query函数呢?
首先,我们需要再每次递归的时候都选择对左子树递归还是对右子树递归,这里和我们平时的有一点不一样
因为权值线段树存储的是数字的个数,所以我们也可以知道左区间数字的个数和右区间数字的个数
如果我们的k>左区间数字的个数,证明第k大肯定在右区间内,反之亦然。
但是有一点需要注意,就是如果我们往右区间递归的话,我们需要让k-两棵树左区间的差值。因为如果我们要往右边递归的话肯定要改变k的大小使得k是对于[l,r]的第k大而不是对于[mid+1,r]的第k大
实在觉得啰嗦的话就可以看成在区间[L,R]里面对值域进行二分
下面是代码:
int query(int l,int r,int L,int R,int k){
if(l==r) return l;
int mid=(l+r)/2;
int tmp=hjt[hjt[R].l].sum-hjt[hjt[L].l].sum;//计算差值,可以结合前缀和的思想来理解
if(k<=tmp) return query(l,mid,hjt[L].l,hjt[R].l,k);
else return query(mid+1,r,hjt[L].r,hjt[R].r,k-tmp);//这里要注意是k-tmp而不是直接k
}
然后是对于上面那一道板子题的AC代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn=5e5+10;
struct node{
int sum,l,r;
}hjt[maxn*40];
int n,m,root[maxn],cnt=0,arr[maxn];
vector<int> v;
int getindex(int val){
return lower_bound(v.begin(),v.end(),val)-v.begin()+1;
}
void insert(int l,int r,int pre,int &now,int p){
hjt[++cnt]=hjt[pre];
now=cnt;
hjt[now].sum++;
if(l==r){
return;
}
int mid=(l+r)/2;
if(p<=mid) insert(l,mid,hjt[pre].l,hjt[now].l,p);
else insert(mid+1,r,hjt[pre].r,hjt[now].r,p);
}
int query(int l,int r,int L,int R,int k){
if(l==r) return l;
int mid=(l+r)/2;
int tmp=hjt[hjt[R].l].sum-hjt[hjt[L].l].sum;
if(k<=tmp) return query(l,mid,hjt[L].l,hjt[R].l,k);
else return query(mid+1,r,hjt[L].r,hjt[R].r,k-tmp);
}
int main(void){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&arr[i]);
v.push_back(arr[i]);
}
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
for(int i=1;i<=n;i++){
insert(1,n,root[i-1],root[i],getindex(arr[i]));
}
while(m--){
int l,r,k;
scanf("%d %d %d",&l,&r,&k);
printf("%d\n",v[query(1,n,root[l-1],root[r],k)-1]);//这里要注意,为了让vector下标对应所以要-1
}
}
可持久化数组
其实我觉得可持久化树组这个名字更好
这里又有一道题(其实就是板子题):
可持久化数组
题目已经很清楚地告诉我们,要使用可持久化线段树/可持久化平衡树,这里我们就使用可持久化线段树就好了。
其实和主席树差不多(基本上一样),就是我们不用建立权值线段树,改成建立普通线段树就好了,接着把离散化给去掉。唯一要注意的地方就是要写build函数,因为权值线段树的初始状态都是0(权值线段树是以值域来划分的,但是初始状态下每一个数字的数量都是0),但是普通线段树就不是了,其他地方和主席树一样
这里的线段树不需要维护任何东西,叶子节点以外的节点就让他空着罢了
还有一点,对于这道题的两个操作(询问历史+修改历史)来说,题目要求都要创立一个新版本(包括询问),所以我们要注意在询问完了之后使得当前新开的根节点=历史询问的根节点(反正询问前后又不会对历史版本有什么修改 ,直接白嫖过来岂不美哉? )
代码也贴一下,顺便标注了一些重要的地方:
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e6+10;
struct node {
int l,r,sum;
} t[maxn*40];
int n,m,arr[maxn],cnt,root[maxn];
void build(int l,int r,int &now) {//build函数和普通线段树没什么区别
now=++cnt;
if(l==r) {
t[now].sum=arr[l];
return;
}
int mid=(l+r)/2;
build(l,mid,t[now].l);
build(mid+1,r,t[now].r);
}
void modify(int l,int r,int ver,int &now,int pos,int num){
now=++cnt;
t[now]=t[ver];
if(l==r){
t[now].sum=num;
return;
}
int mid=(l+r)/2;
if(pos<=mid) modify(l,mid,t[ver].l,t[now].l,pos,num);
else modify(mid+1,r,t[ver].r,t[now].r,pos,num);
}
int query(int l,int r,int now,int pos){
if(l==r) return t[now].sum;
int mid=(l+r)/2;
if(pos<=mid) return query(l,mid,t[now].l,pos);
else return query(mid+1,r,t[now].r,pos);
}
int main(void) {
scanf("%d %d",&n,&m);
for(int i=1; i<=n; i++) {
scanf("%d",&arr[i]);
}
build(1,n,root[0]);
for(int i=1; i<=m; i++) {//因为每一个操作都会对应着一个新版本,也就是说我们执行完程序之后肯定会有m个新版本,所以我们的root[i]表示的就是最新的版本的根
int ver,opt,loc,val;
scanf("%d %d",&ver,&opt);
if(opt==1) {
scanf("%d %d",&loc,&val);
modify(1,n,root[ver],root[i],loc,val);
} else {
scanf("%d",&loc);
printf("%d\n",query(1,n,root[ver],loc));
root[i]=root[ver];//这里我们也要创立一个新版本
}
}
}
BTW,有一个东西叫做rope,是一种GNU扩展,是一种可持久化数组
实现方式应该(大概?)是是块状链表
这种扩展的好处就是简单易用, (开个O2) 可以写掉一些题
坏处就是过度封装导致的效率稍低
开头写两句就可以用了:
#include<ext/rope>
using namespace __gnu_cxx;
rope<char>a;
rope最好的一点就是支持O(1)拷贝历史版本
这玩意儿似乎并不是pb_ds里面的,我在文档里面找了好久都没找到,但是好多文章都说是pb_ds,可能是我太菜了。。。如果对这里有一点了解的dalao欢迎告诉我
c++语法没好好学的后果↑




