单调栈应用——最大全1子矩阵

Update:那个例子哪里感觉一开始写的还是有点歧义，所以就稍微改了一下(2020/03/16)

正文：
在网上看了很多博客，感觉都写的有一点模糊(可能是我太蒻了看不懂dalao们的描述方式)，这里我自己写一篇个人认为比较详细的解法

先看一道例题：P4147 玉蟾宫

题意大概是给你一个只含有字符'F'或者是'R'的矩阵，要找出其中的一个只含字符'F'的面积最大的子矩阵的面积(具体的去看一看原题吧)。

这道题的解法主要是悬线法和单调栈，这里我们只介绍单调栈的做法。

什么是单调栈

单调栈栈内所有元素都呈严格单调性(单调递增或者是单调递减)，那么对于某一个元素x,如果我们要把x入栈，分为以下两种情况（这里假设是一个严格单调递增的单调栈）：

1.若s.top()<x,我们直接push进去

2.若s.top()>=x，我们不停地pop掉栈顶元素直到s.top()<x

如何解题

首先，我们预处理出一个矩阵f, f[i][j]代表了在原矩阵m的m[i][j]位置往上连续的F的数量(包含其本身)，给一张图来看一下：

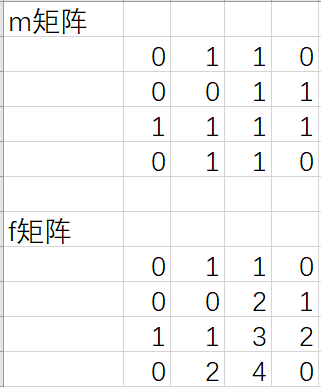
那么根据这个性质，我们可以很快地写出预处理f矩阵的代码：

	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>c;
			if(c=='F') f[i][j]=f[i-1][j]+1;
		}
	}

我们可以发现一个问题，对于f内的任意一个元素f[i][j]进行扩展，扩展的规则就是在这个元素的同一行向左和向右能找到的，连续的，值不低于它的节点的数量*f[i][j]就会得到一个高为f[i][j]且底边包含f[i][j]的最大子矩阵的面积，给一些图来看一下(黄色节点是f[i][j]，而绿色节点是f[i][j]可以扩展到的节点)：

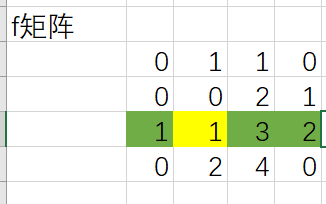
\(S=(1 + 2 + 1)*1=4\)
1是向左扩展的长度
2是向右扩展的长度
接着的一个1是节点本身的长度
外面的一个1是f[i][j]的值

再来一个：

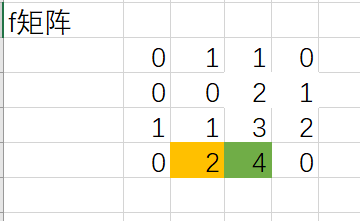
2可以往右扩展到4，但是继续的化就会碰到0，同样的，往左就会立刻碰到0。

\(S=(0 + 1 + 1)*2=4\)
0是向左扩展的长度
1是向右扩展的长度
下面的一个1是节点本身的长度
2是f[i][j]本身的值

使用单调栈

我们这里要一行一行地处理f数组，先建立一个数组a, 包含两个元素，a[i].h描述了在这一行目前第i个矩形的高度，a[i].l描述了目前这个矩形的宽度。很明显的是如果矩形高度是严格递增的化，那么每一个矩形宽度肯定是1（因为无法和前面的矩形合并成一个新的矩形），但是如果此时有一个f[x][i]<=s.top().l的，也就是说我们可以用它来更新最大矩形。那么用它能更新到多大呢？就是当s.top().l比它大的时候都可以更新。所以我们要pop直到找到s.top().l比它小，这就是单调栈。

如果我们一直走到f[x][m]的末尾，但是栈不为空，此时我们也要不停地去更新最大值直到栈空

具体的看代码吧：

void gao(int x){//处理第x行
	memset(a,0,sizeof(a));
	while(!s.empty()) s.pop();
	a[1].h=f[x][1],a[1].l=1;//初始化第一个元素
	s.push(a[1]);//元素入栈
	for(int i=2;i<=m;i++){
		int w=0;
		while(!s.empty()&&f[x][i]<=s.top().h){//单调栈的基操
			w+=s.top().l;//这里我们用w变量来记录已经走过的矩形的宽度，用以留给栈内下一个矩形来更新ans
			ans=max(ans,s.top().h*w);
			s.pop();
		}
		a[i].h=f[x][i];//处理a数组
		a[i].l=w+1;//要给w+1,此时a[i].l代表了高为a[i].h矩形的宽度
		s.push(a[i]);
	}
	int wt=0;//这里我们换一个变量和前面的区分一下
	while(!s.empty()){//通过pop完栈内元素来跟新ans值
		wt+=s.top().l;//记录宽度
		ans=max(ans,s.top().h*wt);
		s.pop();
	}
}

注释在程序里面写的非常详细了(大概？)，还是不懂的化可以自己带入一些数值调试

AC代码：

//Luogu P4147
#include <bits/stdc++.h>
using namespace std;
const int maxn=1926;
struct node{
	int l,h;
}a[maxn];
stack<node> s;
int f[maxn][maxn],m,n,ans;
char c;
void gao(int x){
	memset(a,0,sizeof(a));
	while(!s.empty()) s.pop();
	a[1].h=f[x][1],a[1].l=1;
	s.push(a[1]);
	for(int i=2;i<=m;i++){//这里一定要记住是m，我就是因为写成了n所以WA了好久
		int w=0;
		while(!s.empty()&&f[x][i]<=s.top().h){
			w+=s.top().l;
			ans=max(ans,s.top().h*w);
			s.pop();
		}
		a[i].h=f[x][i];
		a[i].l=w+1;
		s.push(a[i]);
	}
	int wt=0;
	while(!s.empty()){
		wt+=s.top().l;
		ans=max(ans,s.top().h*wt);
		s.pop();
	}
}
int main(void){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>c;
			if(c=='F') f[i][j]=f[i-1][j]+1;
		}
	}
	for(int i=1;i<=n;i++){
		gao(i);//分成每一行处理，因为每一行的状态是独立于下一行的
	}
	printf("%d",ans*3);//别忘了*3哦
}

无用的碎碎念

话说这道题搞了我好久，不管是在网上查资料还是手动模拟。。。也许我不是很擅长这种类型的题目QAQ。从上一次比赛到现在我都没怎么刷题了，都在写博客。