可并堆之——左偏树
其实pb_ds里面内置了可并堆
相信大多数人都知道c++提供了强大的STL, 并且STL里面有一个很好用的priority_queue可以用来充当堆的功能。但是由于STL的过度封装,导致priority_queue无法高效地完成堆和堆之间的合并(一个一个push可不叫高效)。如果题目中涉及到堆的合并问题我们还得手写一个可并堆。一般来讲可并堆主要有3种——配对堆,斐波那契堆和左偏树,斐波那契堆码量太大不适合在竞赛中使用,所以我们一般只考虑配对堆或左偏树,本文主要关于左偏树。
本文的可并堆维护的是序列最小值
什么是左偏树
顾名思义,左偏树是一个向左倾斜的树。虽然这句话是一句废话,但是依然有一个点值得我们去注意:什么是倾斜?我们引入一个距离的概念。假如说堆上有一个节点u,它的儿子是不完全的,也就是说要么没有左儿子要么没有右儿子要么都没有,那么我们说这个节点的距离是0(空节点的距离是-1),这个节点被称作“外节点”。那么对于任意一个点来说,它的距离就是在它的子树中这个点和离他最近的外界点之间的距离。稍微总结一下:
1.左偏树有(假设这里是根保存最小值):
左偏树具有堆的性质,如果变成一棵完全二叉树的化就是一个堆
2.左偏性质,意思就是说树中任意节点x都有:
推论:左偏树里面任意节点x的距离有:
放一张图来看一下:

节点里面的是值,外面的是距离(这玩意儿左偏?)
用merge维护左偏性质
这里我们通过merge操作来维护左偏性质。(和fhq treap一样)
首先,我们判断一下要合并的两棵树有没有空树
其次,现在我们有2棵树,树根是x和y,如果val(x)<val(y)(如果不是的化我们就swap(x,y)),那么可以想到最后合并的树根还是x,所以我们把\(x_r\)和y递归地合并。
合并完了之后,可能会存在不符合左偏性质的情况,这个时候我们只要swap(\(x_l,x_r\))就好了。
最后更新一下dist值就万事大吉了
从别的博客里面找来的图片(真的佩服做动图的dalao):
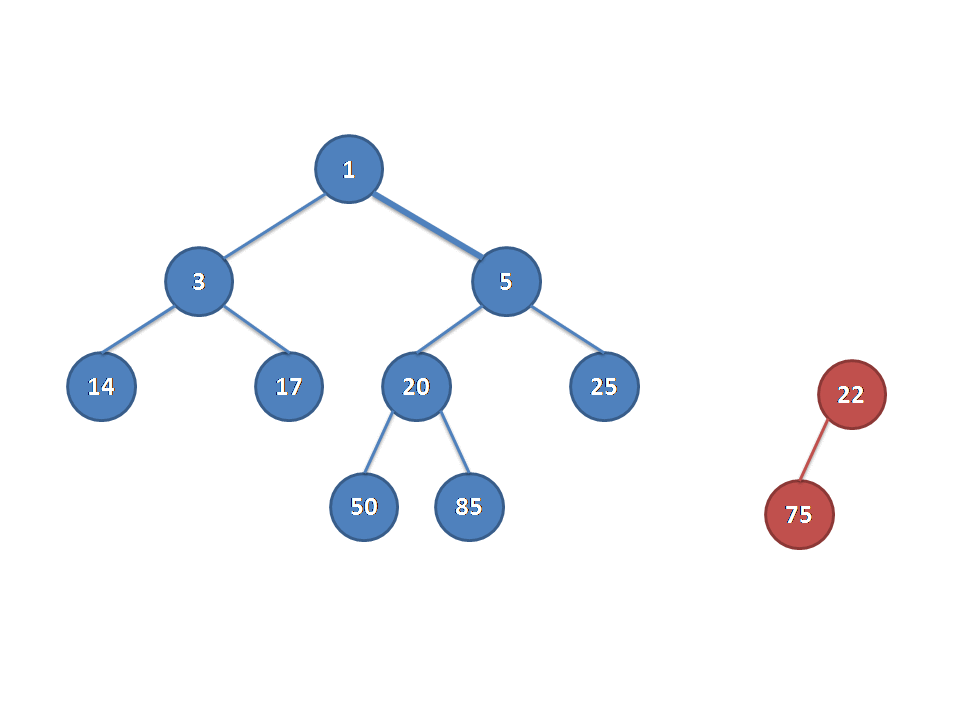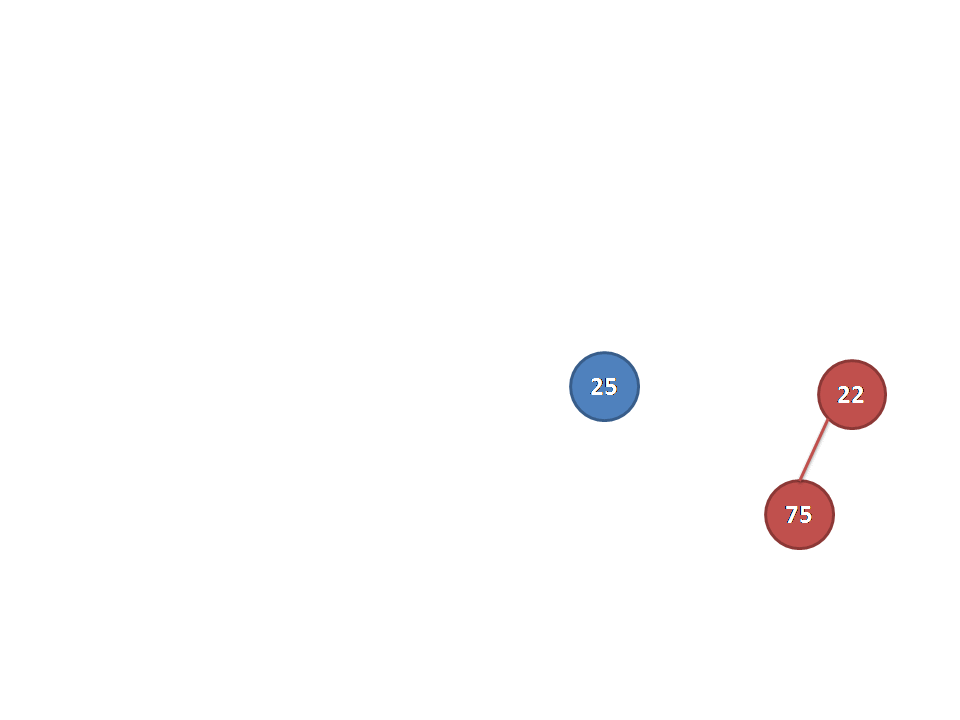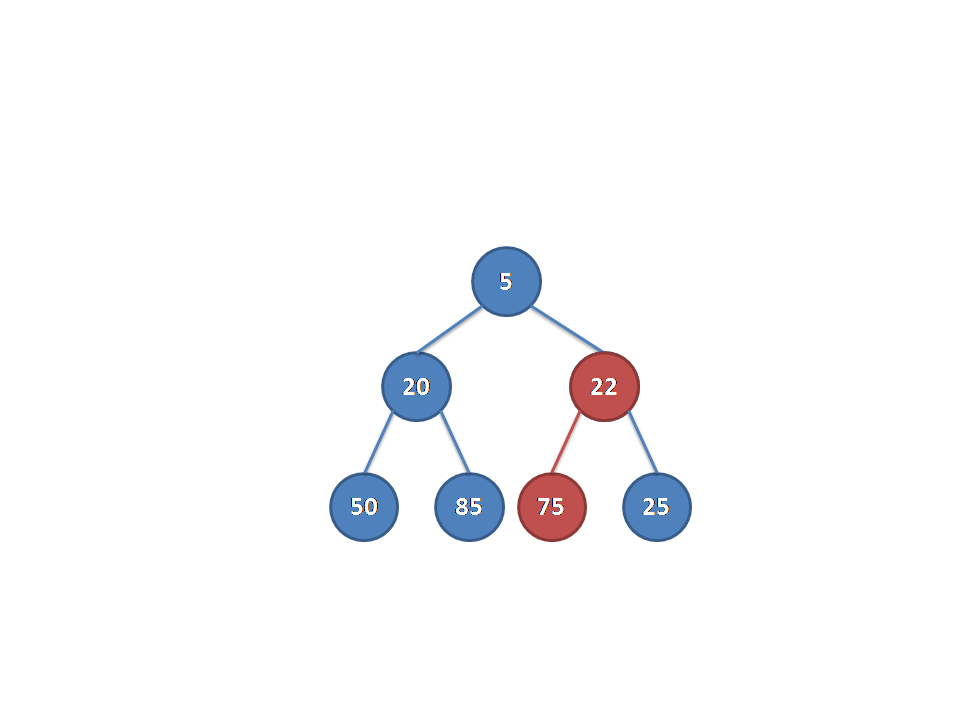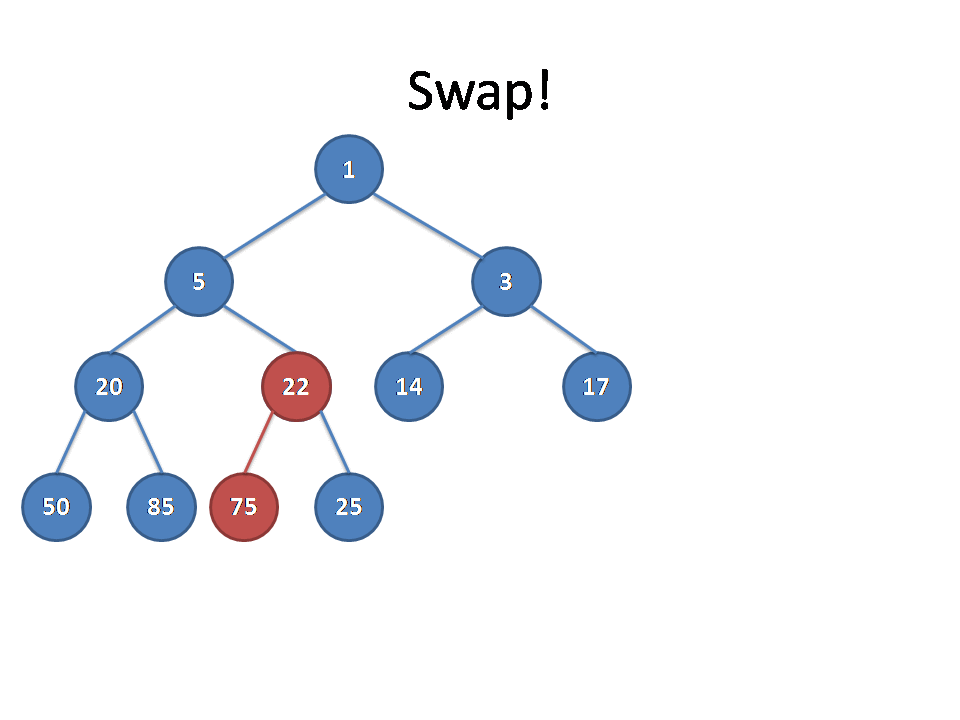
放一下代码:
struct node{
int val,l,r,dis,fa;//这里的fa以后有用,在这里暂时可以不看
}ltt[maxn];
merge的代码:
int merge(int x,int y){
if(!x||!y) return x+y;//和fhq一样
if(ltt[x].val>ltt[y].val||(ltt[x].val==ltt[y].val&&x>y)) swap(x,y);
ltt[x].r=merge(ltt[x].r,y);//合并右节点
ltt[ltt[x].r].fa=x;//这行代码以后有用
if(ltt[ltt[x].l].dis<ltt[ltt[x].r].dis) swap(ltt[x].l,ltt[x].r);//维护左偏性质
ltt[x].dis=ltt[ltt[x].r].dis+1;//更新dis
return x;//返回新树树根
}
各位酌情在开头define一个ls(x),否则代码就会像我写的这么恶心
pop操作
其实很简单,主要就是我们把x的左儿子和右儿子给合并一下然后把这个点标记为删除就好了。
有一道不一般的板子题,建议看一下,也是对前面的几行没有解释的代码的解释:
当我们涉及到合并的时候,事情就变得麻烦了起来。因为我们不仅仅是要把两个堆合并成一个,我们还需要支持对于任意一个元素x,把它所在的堆和另一个元素y所在的堆合并。那么我们如何查找它们各自所在的堆的堆顶呢?这里我们考虑并查集,可以看到,在merge的代码里面已经在维护一个堆之间的并查集了。只要查到x所在堆的堆顶x1,y所在堆的堆顶y1,然后合并x1,y1就好了。
BTW,并查集的路径压缩并不会影响堆的结构,原理可以自行分析一下。
pop代码:
void pop(int x){
ltt[x].val=-1;
ltt[ltt[x].l].fa=ltt[x].l;
ltt[ltt[x].r].fa=ltt[x].r;
ltt[x].fa=merge(ltt[x].l,ltt[x].r);
}
这里要保证如果树根被删掉了的化一定要把新树根节点的fa给更新,否则整棵树最后会指向一个已经删掉了的节点
push操作
push操作非常简单,我们只用看作把一棵大小只有1的左偏树(1个节点)合并到另一棵左偏树上面去就好了
板子题AC代码:
//luogu p3377
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
struct node{
int val,l,r,dis,fa;
}ltt[maxn];
int n,m;
int merge(int x,int y){
if(!x||!y) return x+y;
if(ltt[x].val>ltt[y].val||(ltt[x].val==ltt[y].val&&x>y)) swap(x,y);
ltt[x].r=merge(ltt[x].r,y);
ltt[ltt[x].r].fa=x;
if(ltt[ltt[x].l].dis<ltt[ltt[x].r].dis) swap(ltt[x].l,ltt[x].r);
ltt[x].dis=ltt[ltt[x].r].dis+1;
return x;
}
int find(int x){
return ltt[x].fa==x?x:ltt[x].fa=find(ltt[x].fa);
}
void pop(int x){
ltt[x].val=-1;//这道题里面我们通过val=-1来标记已删除节点
ltt[ltt[x].l].fa=ltt[x].l;
ltt[ltt[x].r].fa=ltt[x].r;
ltt[x].fa=merge(ltt[x].l,ltt[x].r);
}
int main(void){
scanf("%d %d",&n,&m);
ltt[0].dis=-1;
for(int i=1;i<=n;i++){
scanf("%d",<t[i].val);
ltt[i].fa=i;//一定要记得初始化并查集
}
while(m--){
int opt,x,y;
scanf("%d",&opt);
if(opt==1){
scanf("%d %d",&x,&y);
if(ltt[x].val==-1||ltt[y].val==-1) continue;
int x1=find(x),y1=find(y);
if(x1==y1) continue;
ltt[x1].fa=ltt[y1].fa=merge(x1,y1);
}else{
scanf("%d",&x);
if(ltt[x].val==-1){
printf("-1\n");
}else{
int x1=find(x);
printf("%d\n",ltt[x1].val);
pop(x1);
}
}
}
}
使用pb_ds里面的可并堆
首先开头来两句:
#include <ext/pb_ds/priority_queue.hpp>
using namespace __gnu_pbds;
以后用的时候这么声明:
__gnu_pbds::priority_queue <int> q;
这里需要注意一下,因为stl里面也有priority_queue,所以在调用pb_ds里面的priority_queue的时候还是要在前面加上__gnu_pbds:: (当然你也可以不用bits/stdc++)
合并就是直接a.join(b)
总结
总的来说还是相对比较简单的一个数据结构(比某些毒瘤要友好的不能太多),反正也很少会有题目专门只考可并堆
关于为什么左偏树合并的时候非要在右儿子上进行递归而不是左儿子,个人觉得实际上这里是一种启发式合并的运用。启发式合并是一种序列合并思想,在很多其他的数据结构里面也会涉及到
时间复杂度的化,合并是\(O(size_a+size_b)\),push是O(logn),pop也是O(logn)
Reference
https://blog.csdn.net/wang3312362136/article/details/80615874



