树上的简单操作——树链剖分
某神犇:树链剖分什么垃圾,能做的LCT都能做,不能做的LCT也能做
前置条件:
线段树,(都会线段树了应该知道什么是树吧)
前言
现在考虑一棵树,每个节点都有一个点权,要求给x到y路径上的点都加上k,这个问题可以用树上差分很简单地在O(m+n)的复杂度内解决。再考虑一个问题,要求查找树上x到y这条路径上的权值和,也可以先求出每个点到根的dis,然后求出x和y的LCA,最后用公式:dis(x,y)=dis(x,root)+dis(y,root)-2*dis(LCA,root)简单地在O(mlogn+n)的时间内解决。那如果我们把着两种操作整合在一起呢?树链剖分就这么诞生出来了。
正篇
树链剖分,顾名思义,就是把一棵树残忍地剖成一条一条链,然后通过链之间的特性来用某些数据结构去维护它们。我们剖树的时候通常会遵循两大准则:重链剖分和实链剖分,本文暂时只讨论重链剖分。
一般来讲树链剖分的码量都很大,所以可以看作是一种模拟
重链
说到重链,我们先谈谈什么是重儿子。对于某一个树上节点u,它的重儿子就是它儿子里面那个size最大的儿子。可以看成,一个节点只能有一个重儿子,而其他的儿子被称作轻儿子。又重儿子组成的链叫做重链,由轻儿子组成的链叫做轻链。
来张图康康,重链都被加粗显示了:
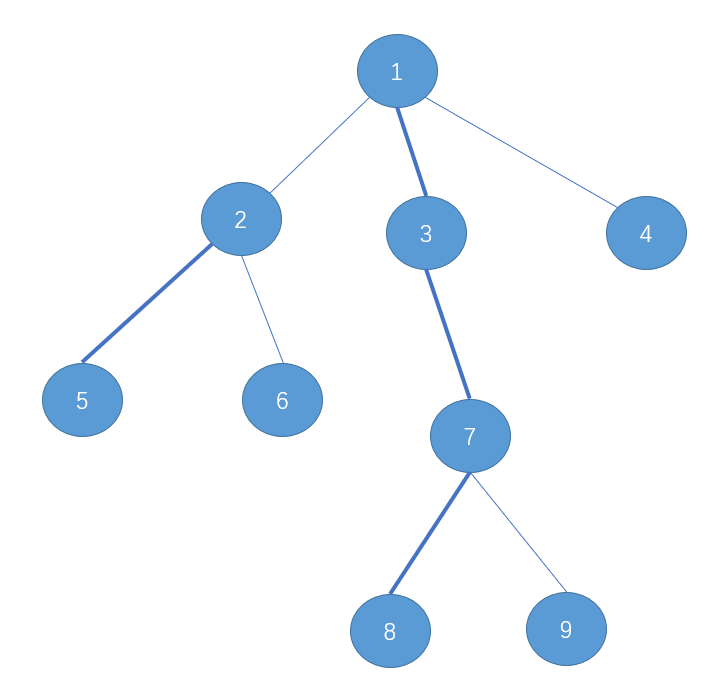
在这张图里面,我们可以看到,1的儿子中3的size更大,所以1->3就被划分成了一条重链,同样,虽然1->2不是重链,但是2->5也可以是重链这样整棵树就被划分成了重链和轻链。
具体程序
首先,我们先声明一些变量:
int size[maxn],dep[maxn],f[maxn],hson[maxn];
size就是子树大小,dep是节点深度,f是节点父亲,hson是节点的重儿子
接着,我们开始写第一个dfs:
void dfs1(int u,int fa,int d){
size[u]=1;
f[u]=fa;
dep[u]=d;
int maxs=-1;
for(int i=0;i<gpe[u].size();i++){
int v=gpe[u][i];
if(v==fa) continue;
dfs1(v,u,d+1);
size[u]+=size[v];
if(size[v]>maxs) hson[u]=v,maxs=size[v];
}
}
整个程序还是非常简单的,我们已经处理出来了整棵树的一些基本信息,那么我们现在就要开始把链整合在一起了。
第二个dfs: 这里我们引入一个dfs序的东西。
其实也蛮简单,就是对于某一个节点u,它在dfs的过程中被访问到的顺序,再来张图:

可能有人会问,图是不是错了啊,因为id[2]不应该是2吗,为什么id[3]是2啊?因为我们有一个规定,在第二次dfs的时候优先对重儿子进行搜索。因为我们必须保证任何一条重链上的点的dfs序是连续的,如果我们优先搜索2,那么3的dfs序就是5了,和1的dfs序不连续,也就失去了意义。我们还要对每一条重链进行标识。或者是说,对于某一个点u,我们要给出它所在的重链的顶部节点(轻节点的顶部节点是其本身),这里我们用top[u]来表示顶部节点。再最后,我们把点值也转移到另外一个数组里面。具体细节看程序吧,反正也不是很长:
int id[maxn],wt[maxn],top[maxn],cnt=0;
void dfs2(int u,int tc){
id[u]=++cnt;
wt[cnt]=a[u];
top[u]=tc;
if(!hson[u]) return;
dfs2(hson[u],tc);
for(int i=0;i<gpe[u].size();i++){
int v=gpe[u][i];
if(v==f[u]||v==hson[u]) continue;
dfs2(v,v);
}
}
id就是dfs序,wt是原点值a的转换,top就是链顶,cnt是用来计算dfs序的。
通过观察上面的图,我们发现,对于某一条链,可以把它拆成重链和轻链的组合,虽然我们没办法维护轻链,因为它们的dfs序并不连续,但是重链的dfs序是连续的。如果提到维护数列的区间和,那么我们肯定会想到 (分块) 线段树。接下来就是套一个线段树的模板了,这里就不多说,直接上代码:
struct node{
ll sum,tag;
}t[maxn*2];
ll ans=0;
void update(ll pos){
t[pos].sum=(t[pos<<1].sum+t[pos<<1|1].sum)%MOD;
}
void build(ll l,ll r,ll pos){
if(l==r){
t[pos].sum=wt[l];
return;
}
ll mid=(l+r)/2;
build(l,mid,pos<<1);
build(mid+1,r,pos<<1|1);
update(pos);
}
void change(ll pos,ll l,ll r,ll k)
{
t[pos].tag=(t[pos].tag+k)%MOD;
t[pos].sum=(t[pos].sum+k*(r-l+1))%MOD;
}
void pushdown(ll l,ll r,ll pos){
if(!t[pos].tag) return;
ll mid=(l+r)/2;
change(pos<<1,l,mid,t[pos].tag);
change(pos<<1|1,mid+1,r,t[pos].tag);
t[pos].tag=0;
}
void add(ll tl,ll tr,ll l,ll r,ll v,ll pos){
if(tl<=l&&tr>=r){
t[pos].sum+=v*(r-l+1);
t[pos].tag+=v;
return;
}
if(r<tl||l>tr){
return;
}
ll mid=(l+r)/2;
pushdown(l,r,pos);
add(tl,tr,l,mid,v,pos<<1);
add(tl,tr,mid+1,r,v,pos<<1|1);
update(pos);
}
void query(ll tl,ll tr,ll l,ll r,ll pos){
if(tl<=l&&tr>=r){
ans+=t[pos].sum;
ans%=MOD;
return;
}
if(r<tl||l>tr){
return;
}
ll mid=(l+r)/2;
pushdown(l,r,pos);
query(tl,tr,l,mid,pos<<1);
query(tl,tr,mid+1,r,pos<<1|1);
return;
}
那么,对于某一个询问x和y之间的点值之和的询问,我们可以把它分成两部分:
- x到top[x]的重链区间和
- top[x]到top[y]的轻链和
- top[y]到y的重链和
其实现实中情况比这个复杂,打个比方,有一种很奇怪的食物,两块面包中间由一根面条连接(?)我们可以一口吃掉一块面包O(logn),但是吃面条要用到O(n),那么我们最简单的想法就是从这种奇怪的食物的某一个节点id[x]吃到id[top[x]]来吃掉一个面包(重链),然后从id[top[x]]到f[top[x]]去吃掉一根面条(轻链),就这么下去直到吃掉最后一块面包。程序如下:
int c_ask(int x,int y){
int ret=0;
ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
query(id[top[x]],id[x],1,n,1);
ret=(ret+ans)%MOD;
ans=0;
x=f[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
query(id[x],id[y],1,n,1);
ret=(ret+ans)%MOD;
ans=0;
return ret;
}
(由于我线段树板子写的太恶心所以要一遍一遍地重置ans值,但是我懒得改了)
链上修改也很简单,照着套就完事了:
void c_add(int x,int y,int val){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
add(id[top[x]],id[x],1,n,val,1);
x=f[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
add(id[x],id[y],1,n,val,1);
}
再就是子树修改:
add(id[x],id[x]+size[x]-1,1,n,v%MOD,1);
因为实际上一棵子树的dfs序也是连续的,可以自己手动模拟一下,所以就是简单地加上size[x]-1就好了
子树查询:
query(id[x],id[x]+size[x]-1,1,n,1);
一道模板题:https://www.luogu.com.cn/problem/P3384
AC代码:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=2*1e6+10;
vector<int> gpe[maxn];
int a[maxn],n,m,r,MOD;
int size[maxn],dep[maxn],f[maxn],hson[maxn];
void dfs1(int u,int fa,int d){
size[u]=1;
f[u]=fa;
dep[u]=d;
int maxs=-1;
for(int i=0;i<gpe[u].size();i++){
int v=gpe[u][i];
if(v==fa) continue;
dfs1(v,u,d+1);
size[u]+=size[v];
if(size[v]>maxs) hson[u]=v,maxs=size[v];
}
}
int id[maxn],wt[maxn],top[maxn],cnt=0;
void dfs2(int u,int tc){
id[u]=++cnt;
wt[cnt]=a[u];
top[u]=tc;
if(!hson[u]) return;
dfs2(hson[u],tc);
for(int i=0;i<gpe[u].size();i++){
int v=gpe[u][i];
if(v==f[u]||v==hson[u]) continue;
dfs2(v,v);
}
}
struct node{
ll sum,tag;
}t[maxn*2];
ll ans=0;
void update(ll pos){
t[pos].sum=(t[pos<<1].sum+t[pos<<1|1].sum)%MOD;
}
void build(ll l,ll r,ll pos){
if(l==r){
t[pos].sum=wt[l];
return;
}
ll mid=(l+r)/2;
build(l,mid,pos<<1);
build(mid+1,r,pos<<1|1);
update(pos);
}
void change(ll pos,ll l,ll r,ll k)
{
t[pos].tag=(t[pos].tag+k)%MOD;
t[pos].sum=(t[pos].sum+k*(r-l+1))%MOD;
}
void pushdown(ll l,ll r,ll pos){
if(!t[pos].tag) return;
ll mid=(l+r)/2;
change(pos<<1,l,mid,t[pos].tag);
change(pos<<1|1,mid+1,r,t[pos].tag);
t[pos].tag=0;
}
void add(ll tl,ll tr,ll l,ll r,ll v,ll pos){
if(tl<=l&&tr>=r){
t[pos].sum+=v*(r-l+1);
t[pos].tag+=v;
return;
}
if(r<tl||l>tr){
return;
}
ll mid=(l+r)/2;
pushdown(l,r,pos);
add(tl,tr,l,mid,v,pos<<1);
add(tl,tr,mid+1,r,v,pos<<1|1);
update(pos);
}
void query(ll tl,ll tr,ll l,ll r,ll pos){
if(tl<=l&&tr>=r){
ans+=t[pos].sum;
ans%=MOD;
return;
}
if(r<tl||l>tr){
return;
}
ll mid=(l+r)/2;
pushdown(l,r,pos);
query(tl,tr,l,mid,pos<<1);
query(tl,tr,mid+1,r,pos<<1|1);
return;
}
int c_ask(int x,int y){
int ret=0;
ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
query(id[top[x]],id[x],1,n,1);
ret=(ret+ans)%MOD;
ans=0;
x=f[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
query(id[x],id[y],1,n,1);
ret=(ret+ans)%MOD;
ans=0;
return ret;
}
void c_add(int x,int y,int val){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
add(id[top[x]],id[x],1,n,val,1);
x=f[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
add(id[x],id[y],1,n,val,1);
}
int main(void){
scanf("%d %d %d %d",&n,&m,&r,&MOD);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
for(int i=1;i<=n-1;i++){
int u,v;
scanf("%d %d",&u,&v);
gpe[u].push_back(v);
gpe[v].push_back(u);
}
dfs1(r,r,1);
dfs2(r,r);
build(1,n,1);
while(m--){
int opt,x,y,v;
scanf("%d",&opt);
if(opt==1){
scanf("%d %d %d",&x,&y,&v);
c_add(x,y,v);
}else if(opt==2){
scanf("%d %d",&x,&y);
printf("%d\n",c_ask(x,y));
}else if(opt==3){
scanf("%d %d",&x,&v);
add(id[x],id[x]+size[x]-1,1,n,v%MOD,1);
}else{
scanf("%d",&x);
query(id[x],id[x]+size[x]-1,1,n,1);
printf("%d\n",ans);
ans=0;
}
}
}
树链剖分时间复杂度
假设(u,v)是一条轻边,那么size(v)<size(u)/2,并且从根节点到任意节点x之间的路径上轻重链的个数<logn
所以,树链剖分的时间复杂度是O(nlog^2n)



