图论基础知识(1)-什么是图和图的分类
emmm......蒟蒻的第一篇博客,先讲一个比较简单的东西来熟悉以下操作吧(还是怕自己翻车)
由于本人知识水平有限,暂时不会涉及相关数学知识,这篇博客主要还是提供个人对图论的比较感性的认识
这篇文章将要介绍:
- 图的基本定义
- 图的简单分类
- 一些简单术语的解释
因为本人比较蒻,所以这篇博客会讲的非常慢,dalao们可以绕步了。。。
Part1 什么是图:

这是百度百科里面给出的解释,很重要的一条就是:“这种图形通常是用来描述某些事物之间的某种特定关系”,也就是说图实际上存储的是一些关系,所以说以下的两张图:
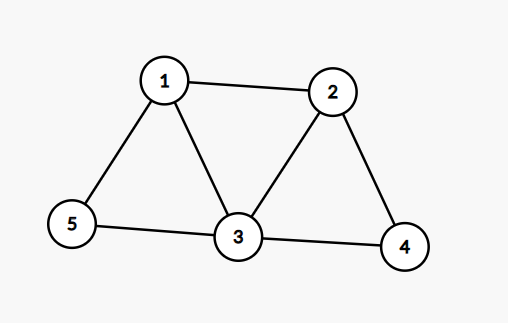
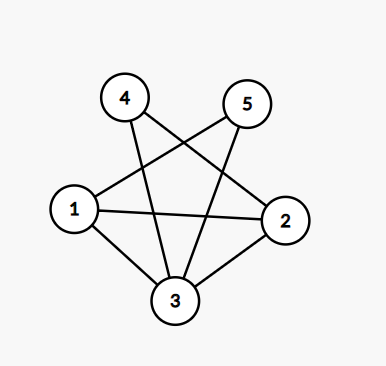
它们其实都是同一张图(仔细数数看?)
因为点和点之间的关系没变,虽然看起来形状完全不一样了,但是点和点之间的关系(连通与不连通)都是没有变化的,所以这两个图都是一样的。
我们有时候会用G=(V,E)来描述一张图,这里的V(vertical)被称作顶点集合(就是1,2,3,4,5这几个点),这里的E(edge)被称作边集合,我们可以很明显地看出,边集合存储的就是点和点之间的关系了
Part2 图的分类:
不得不说,图的分类实在是太多太杂了,我们可以简单地把图分成两类:有向图和无向图
有向图可以简单地理解成是由有向边组成的图,那么我们这里要讨论一下什么是有向边。
我们都知道,图描述的是点与点之间的关系,那么类比于现实世界里面的关系,我们就会发现有三种可能:A和B互相认识(你和你的朋友),A认识B而B不认识A(你和马云),A不认识B但B认识A(你和一群追着你讨债的人),那么我们在图中也要用一种东西来描述这三种关系。通过观察我们可以发现,这3种关系里面有些关系是单向的,有些关系是双向的,所以我们就有了有向边(用来描述单向的关系)和无向边(用来描述双向的关系),下面给出了两个例子:
1和2之间的边是无向边

1和2之间的边是有向边

如果有向边和无向边可以理解了的化,相信有向图和无向图也是非常简单的
Part3. 一些简单术语的解释:
1. 顶点
顶点就是图里面的点(虽然大概都能从前面的介绍里面看出来。。。)
2.边
前面有讲这里就不在赘述了
3.带权图
这个说一下
我们有时候要在图里面添加一些信息让图能更好地描述一件事情。比如说我们说A和B互相认识了3年,我们不仅要描述它们互相认识,还要描述互相认识了3年这个信息。所以我们通过给边加上一个权值来说明他们认识的时间,这种权值我们称之为“边权”。而一幅由带权边组成的图被称作带权图,不管是有向图还是无向图都可以是带权图。
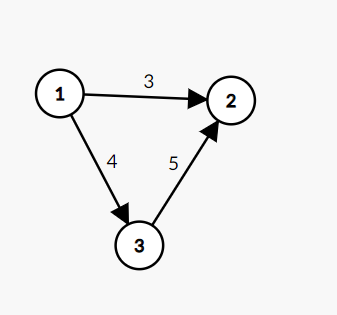
同时我们也要注意,有些带权图的权值不是在边上而是在点上,这种情况我们称这些权值为“点权”
4.顶点的度:
这里我们要分开来讨论一下
无向图里面的度描述的是和顶点A相连的边的数量,比如说这个图:
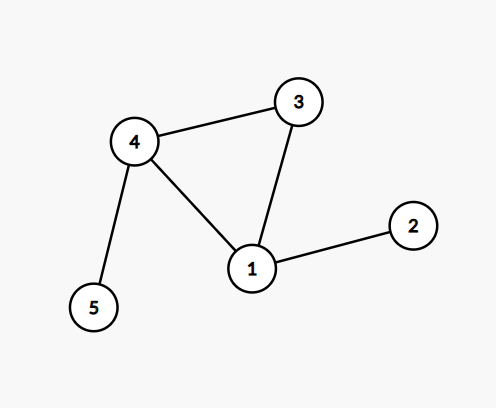
其中点1的度是3,因为一共由3条边和它相连,点3的度是2,因为一共有两条边和它相连
(还是非常简单的)
再来康康有向图:
我们在有向图里面会把度分为入度和出度。入度表示的是和点A相邻的所有边中那些目的地是A的边的数量,出度就是出发点是A的边的数量,举个栗子:
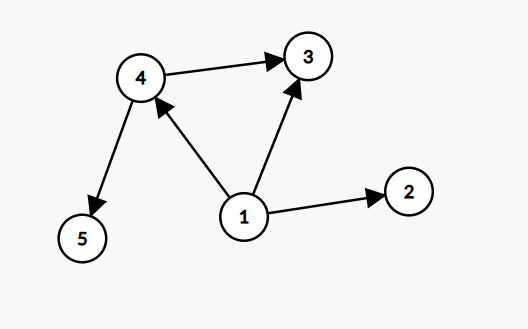
其中点1的入度是0,出度是3;点4的入度是1,出度是2,点3的入度是2,出度是0
5.环
环的特点是环上的任意一点都能通过环到达自己,换言之,环上的任意两点都可以互相到达。
有些环上权值之和为负值,这种环我们称之为负环
6.有向无环图(DAG)
如何字面意思上一样,有向无环图就是一个没有环的有向图(就和上面的图一样),DAG可以和dp紧密地联系起来,同时,dp的状态转移如果画成一幅图的化也是一个DAG。原理可以自行思考
7.重(chong)边
当2个点之间有多余一个的方向相同的边时我们称这两个点之间有重边
一定要记住时chong而不是zhong,否则会和树剖里面的重(zhong)边搞混
8.路径
(话说这么晚讲路径真的没问题吗。。。)
从一个点到另一个点之间所经过的边称为路径,一条简单路径意思是路径上没有环(否则可以通过环绕一圈回到环的起点)
9.连通图
(有没有电信图啊)
无向图中,如果任意两点都可以互相到达则称这幅图为连通图。如果无向图不连通但是它的子图连通我们则称这个子图是连通分量
有向图中,如果任意A和B之间都有一条路径相连,那么我们称这幅图为强连通的
同样的,如果一幅图本身不符合,但是它的子图符合强连通,那么我们称这个子图为强连通分量
总之,连通图是在无向图的基础上对图中顶点之间的连通做了更高的要求,而强连通图是在有向图的基础上对图中顶点的连通做了更高的要求
就先说这么多吧。。。总结一下,要认识到的最重要的几点是:
图表示的是点之间的关系
边权相当于是边的一种附加属性
有向边的意思是A可以到B但是B不能到A
蒟蒻第一次写博客,有不好的地方请无视和我说一下。。。



