平衡树学习笔记
平衡树,启动.
- 改考试题两棵树傻鸟解法改破防了,所以回来总结下
有关平衡树的浅显理解
首先来说平衡树是什么.
依照定义来说,它是二叉搜索树的进阶,它支持去将节点的查询等操作稳定在\(O(log(n))\)的一个均摊复杂度.
怎么理解这个,因为二叉搜索树的最坏情况会被卡成一条链,所有操作变成了\(O(n)\)复杂度.
而平衡树保证二叉树的深度能够在\(log(n)\),这个保证递归深度不会拉长时间开销.
所以平衡树一开始出现就是来解决查询时间开销的问题.
但是因为平衡树的底层实现各不相同,这导致它们衍生出许多二叉搜索树完全难以实现的操作.
所以说平衡树是一种灵活的算法,它能够解决许多问题.
splay
splay就是上述平衡树中的一种,它的实现核心是将树上节点通过若干次旋转来对节点进行操作.
我们先从它出现的目的上来看,splay如何解决时间复杂度GG的问题.
其实说白了,就是在树上左儿子/右儿子深度较另一边过于深时进行旋转变换,以保证深度始终在log范围下.
了解完定义,开始从它的基本操作开始来说.
首先是旋转rotate:
对于一个节点,它与父节点大小关系只有两种,比父节点大或小.
对于大的情况,我们把相对该节点较小的子树代替该节点挂在父节点上,然后将该节点插入到父亲与父亲的父亲之间就行.
小的情况反过来就行.
void rotate(int x){
int y=t[x].fa;
int z=t[y].fa;
int k=t[y].s[1]==x;
t[z].s[t[z].s[1]==y]=x;//x在y右/左
t[x].fa=z;
t[y].s[k]=t[x].s[k^1];//将原先属于x的与x相对y不同的子树接上去.
t[t[x].s[k^1]].fa=y;
t[x].s[k^1]=y;
t[y].fa=x;
pushup(x),pushup(y);
}
为什么是相对大小与父节点相对大小不一样的子树替代挂上.
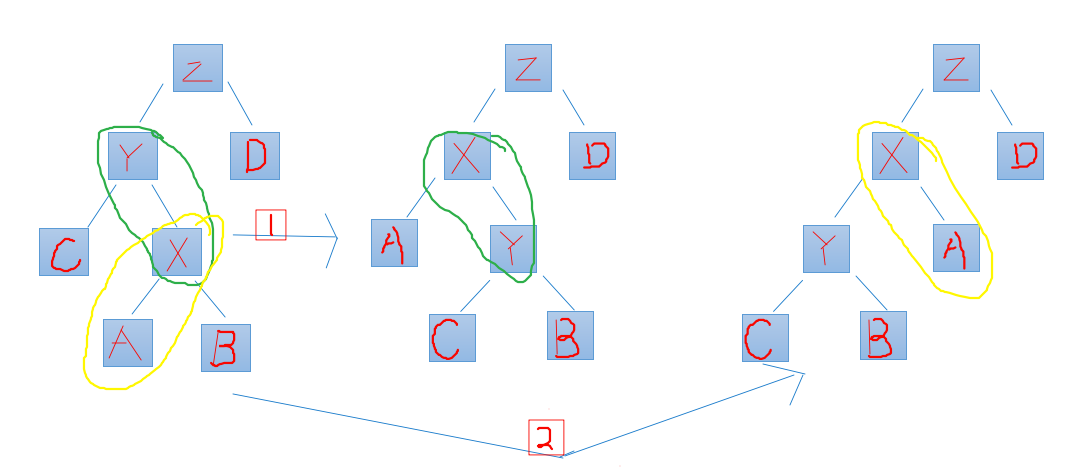
不换儿子的两种情况,平衡的性质都维护不了.
接着是以rotate为基础的移动操作splay:
对于一个节点,如果我们一直单纯按照rotate的方法一路转到根,那么会有一条链不发生更改.
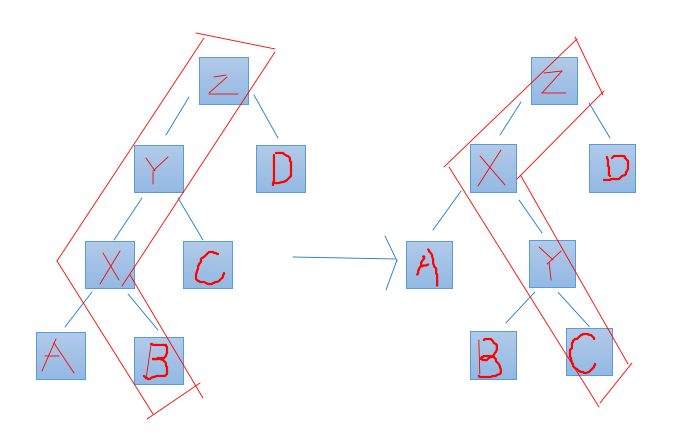
类似于上图,红色是当前不变链,于是这个东西就可能被卡得退化成链.
所以我们就需要对于三个节点在同侧的这种情况进行处理.
先把y放上去,再转x.
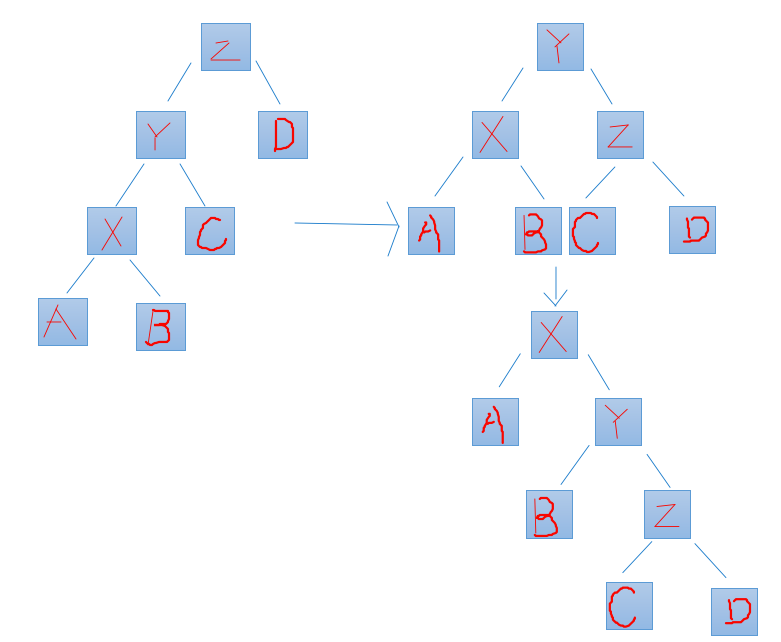
这个时候可以发现处理完毕后,没有一条链是固定不变的.
如果是x与y相对父节点位置不相同的话,转两次x.
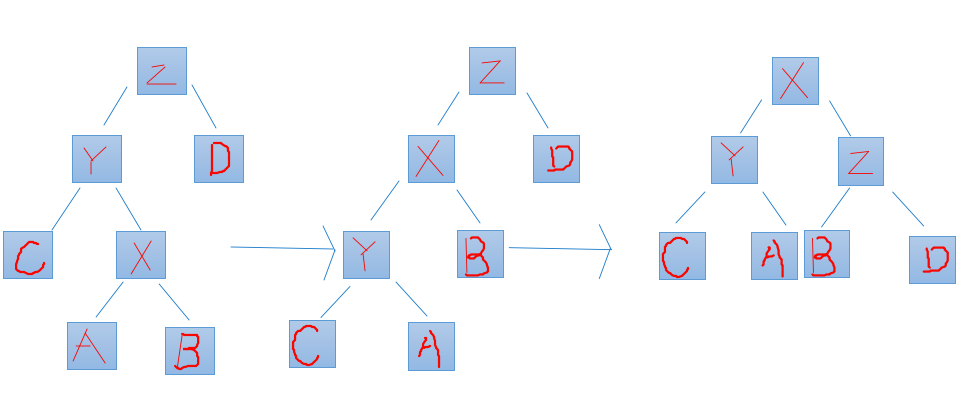
可以发现,我们所需要的就是它整个树没有不动的链,这样保持平衡.
核心的旋转就是这样,剩下的没有什么记录的必要,放一个板子在这里
其实是现在没心情也没时间记录,以后再说吧...
void pushup(int now)
{//更新信息
t[now].size=t[now].cnt;
if(t[now].s[0])t[now].size+=t[t[now].s[0]].size;
if(t[now].s[1])t[now].size+=t[t[now].s[1]].size;
}
void build(){//建树,有的题目中需要,有时可要可不要
rt=tot=1;
t[rt].val=-0x7fffffff;
t[rt].cnt=1;
t[rt].size=1;
}
void rotate(int x){//旋转
int y=t[x].fa;
int z=t[y].fa;
int k=t[y].s[1]==x;
t[z].s[t[z].s[1]==y]=x;//x在y右/左
t[x].fa=z;
t[y].s[k]=t[x].s[k^1];//将原先属于x的与x相对y不同的子树接上去.
t[t[x].s[k^1]].fa=y;
t[x].s[k^1]=y;
t[y].fa=x;
pushup(x),pushup(y);
}
void splay(int x,int to)
{//旋转移动
while(t[x].fa!=to)
{
int y=t[x].fa,z=t[y].fa;
if(z!=to)
(t[z].s[0]==y)^(t[y].s[0]==x)?rotate(x):rotate(y);
rotate(x);
}
if(!to)rt=x;
}
void find(int x)//splay特点,要找到它就把它转上去.
{
int now=rt;
if(!now)return;
while(t[now].s[x>t[now].val]&&x!=t[now].val)
now=t[now].s[x>t[now].val];
splay(now,0);
}
void creat(int x){
int now=rt,fa=0;
while(now&&t[now].val!=x)
fa=now,now=t[now].s[x>t[now].val];
if(now)++t[now].cnt;
else
{
now=++tot;
if(fa)
t[fa].s[x>t[fa].val]=now;
t[now].s[0]=t[now].s[1]=0;
t[now].fa=fa;t[now].val=x;
t[now].cnt=1;t[now].size=1;
}splay(now,0);
}
int f_ne(int x)
{//后继
find(x);
int now=rt;
if(t[now].val>x)return now;
now=t[now].s[1];
while(t[now].s[0])now=t[now].s[0];
return now;
}
int f_pre(int x)
{//前驱
find(x);
int now=rt;
if(t[now].val<x)return now;
now=t[now].s[0];
while(t[now].s[1])now=t[now].s[1];
return now;
}
void del(int x)
{//前驱和后继之间的只有自己,所以有如下删除操作
int pre=f_pre(x),ne=f_ne(x);
splay(pre,0),splay(ne,pre);
int now=t[ne].s[0];
if(t[now].cnt>1)
--t[now].cnt,splay(now,0);
else t[ne].s[0]=0;
pushup(ne),pushup(pre);
}
int get_s(int x)
{
find(x);
return t[t[rt].s[0]].size+(t[rt].val<x);
}
int kth(int x)
{//第k小
int now=rt;
if(t[now].size<x)return 0;
while(1)
{
int tmp=t[now].s[0];
if(t[tmp].size+t[now].cnt<x)
x-=t[tmp].size+t[now].cnt,
now=t[now].s[1];
else if(t[tmp].size<x)return t[now].val;
else now=tmp;
}
}
有个恶心东西好题,千山鸟飞绝,想了一种建两棵树的挠餐解法...
就是因为这个玩意改了两天没改出来,才有了上面的总结.
正解的思路在考场上想到过类似的,没有想到怎么维护,所以放弃了,客观上来说这个题还是很有价值的.
FHQtreap
这个FHQ核心是分裂和合并,代码没有烦人的旋转,就非常棒.
细节和思想理解方面,到时候再说吧,反正不算难,这会懒得打.
#include<bits/stdc++.h>
#define lc t[now].son[0]
#define rc t[now].son[1]
using namespace std;
mt19937 myrand(233);
int tot,rt;
struct treap{
int val,sz,id,son[2];
}t[320983];
inline int creat(int x){
t[++tot].val=x;
t[tot].sz=1;
t[tot].id=myrand();
return tot;
}
inline void pushup(int now){
t[now].sz=t[lc].sz+t[rc].sz+1;
}
void split(int now,int k,int &x,int &y){
if(!now)return void(x=y=0);
if(t[now].val<=k)x=now,split(rc,k,rc,y);//分裂时注意,左子树已经归x,剩下的再分
else y=now,split(lc,k,x,lc);
pushup(now);
}
int merge(int x,int y){
if(!x||!y)return x|y;
if(t[x].id>t[y].id)return t[x].son[1]=merge(t[x].son[1],y),pushup(x),x;
else return t[y].son[0]=merge(x,t[y].son[0]),pushup(y),y;
}
inline void insert(int k){
int x,y;
split(rt,k,x,y);
rt=merge(merge(x,creat(k)),y);
}
inline void del(int k){
int x,y,z;
split(rt,k,x,y);split(x,k-1,x,z);//这里注意是把x分了,别写太快
z=merge(t[z].son[0],t[z].son[1]);rt=merge(merge(x,z),y);
}
inline int rk(int k){
int x,y,ans;
split(rt,k-1,x,y),ans=t[x].sz+1;
return rt=merge(x,y),ans;
}
inline int kth(int now,int k){
while(1){
if(t[lc].sz>=k)now=lc;
else if(t[lc].sz+1==k)return now;
else k-=t[lc].sz+1,now=rc;
}
}
inline int pre(int k){
int x,y,ans;
split(rt,k-1,x,y),ans=t[kth(x,t[x].sz)].val;
return rt=merge(x,y),ans;
}
inline int ne(int k){
int x,y,ans;
split(rt,k,x,y);ans=t[kth(y,1)].val;
return rt=merge(x,y),ans;
}
int main(){
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
int n;
cin>>n;
int op,x;
while(n--){
cin>>op>>x;
if(op==1)insert(x);
if(op==2)del(x);
if(op==3)printf("%d\n",rk(x));
if(op==4)printf("%d\n",t[kth(rt,x)].val);
if(op==5)printf("%d\n",pre(x));
if(op==6)printf("%d\n",ne(x));
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号