干草堆|单调队列优化dp|题解
题面
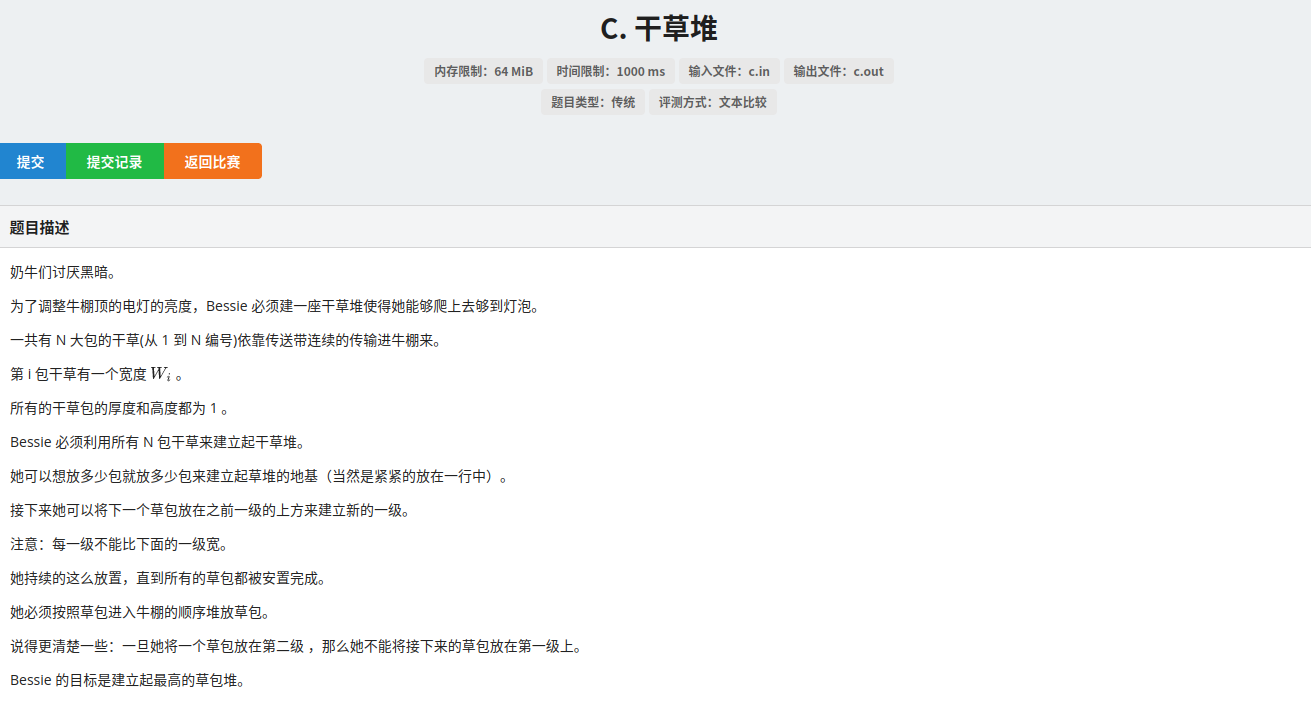
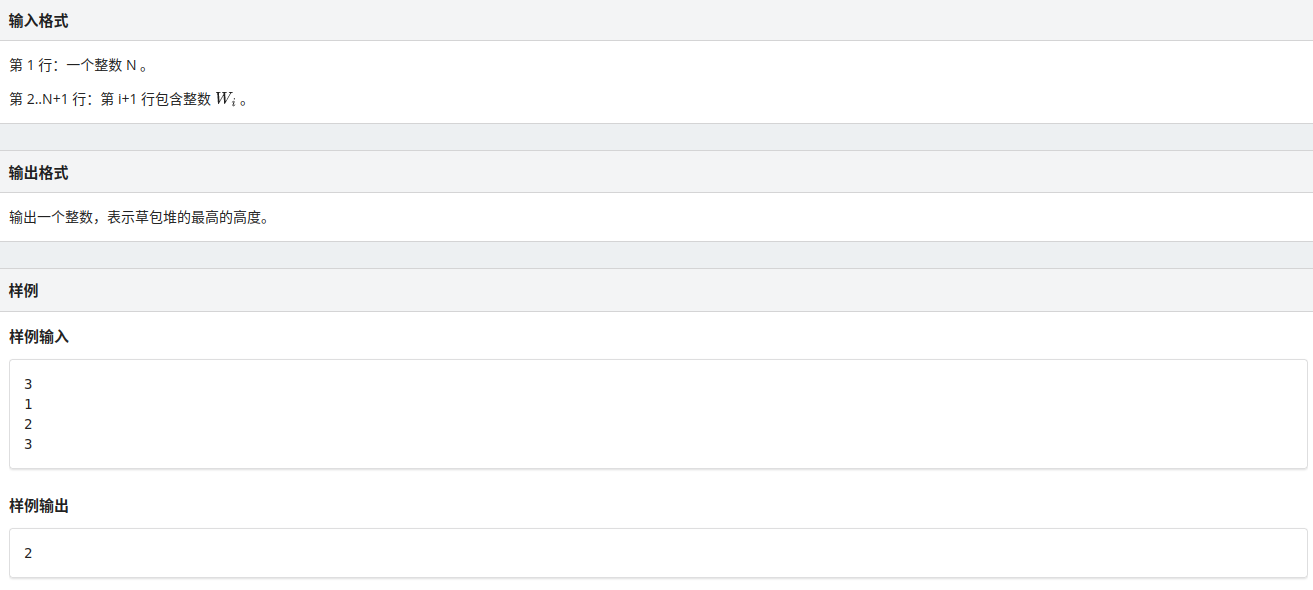
没啥意义的垃圾话.
还剩两个多小时,第一眼看这题,想dp,但是想的是暴力\(O(n^3)\).
构建\(f_{i,j}\)表示上一层最后一个是\(j\),\(j+1->i\)都是本层.
枚举i,j,k,它n1e6范围,肯定又R又T,GG.
所以换思路,想从上往下用尽可能少的草构成一层.
然后大样例没过,思考为什么没过,然后造了个数据发现贪心GG,还剩1小时被迫回到dp.
接着1个小时坐牢+坐牢.
有种喝着putaozher坠机的感觉.
考试时想着正向dp时间复杂度牢大了,就想着从后面开始打一个dp,但是构建状态又出问题.
又思考什么情况下在上层确定最高时,下层最优,肯定上一层最小,但不知道怎么确定最优高度,然后就考试结束,GG.
没敢交贪心代码,就交了\(O(n^3)\)dp,33分,没贪心47分高...
解析
这个问题肯定是从上往下去推的,上层在去选择的时候,它不会出现下层去用一些东西导致上层分配必须更改的.
但是你从下层去推,有些草堆不能当基座,你提前确定下来,那再往上面看,发现它上面的一个就比底座大,你就得更改.
所以是从上往下推,保证状态不会出现错误的情况.
那再思考怎么模拟它选取最优.
我们先假设目前我们得到了一个状态,这个状态总共用了后面的k个草堆,假设我们要最差解,毫无疑问我们把它都放一层.
注:我下面所述的状态变化中说的头个,第二个,第三个,第k个,是倒着数的第几个
那如果这个状态要优化到用k个的最优,首先我们要看头上那个草能不能放到上面去.
如果可以,状态扩展为h=2.
那这个时候我们还想要让它到h=3,怎么办?我们再把一层的第二个东西放上去.
这个时候,如果我们第二个东西>第一个东西的宽度,那我们就可以把第一个东西放到第二个上面,构成一个h=3的状态.
那不能怎么办?再从底下移上来一个东西,看它加上第二个的宽度满不满足条件,让第一个能放上去.
这样我们一直从底层去取东西,一层层往上堆,这包可以得到我们的最优高度状态.
这时我们再思考往这个状态里面新加一个东西,就是说,我们现在用k+1个物品构建状态.
它肯定是放在最后面了,这个物品必定在最下层,那我们肯定是要重复这个过程再使高度最高,没问题吧.
如果说我们前面使得k状态的高度最优,不考虑最下面的宽度问题,那么我们新加进来第k+1个东西时,还要重复上述过程,
直到之前的那层更窄时,我们会得到一个最利于答案增加的状态.
所以可以知道,在我们当前状态最高的时候,不一定底层最窄(可能还可以往上移动物品),但在底层最窄时,
我们必须要求上层尽可能的窄去满足这个条件,同时上层要窄,就要求其上层能够尽可能窄.
这样一看,当我们每一层都做到最窄的时候,
就是我们重复"再从底下移上来一个东西,看它加上第二个的宽度满不满足条件,让第一个能放上去."这一步的结果.
这样最终就导致了最高安排.图解过程...等我到时候换到windows再说吧.
如此我们找到了一个绝对是最优的情况---每一层都最窄.
那么尝试构建一个状转方程,用\(f_i\)表示后面i个东西构成的最优状态,在最优状态之下的最下层宽度是\(g_i\).
发现有状转方程:
考虑当j越小时,底层宽度(i->j-1)越小,所以要取满足条件的最小j取扩展.
条件可以转换成\(sum_{j-1}-g_j>=sum_{i-1}\)
同时有\(sum_{i-1}\)随i减少单调递减,而\(sum_{j-1}-g_j\)是定值,所以只要一个决策开始生效,之后一直可生效.
但是我们应该"取满足条件的最小j取扩展"(f),所以明显可以单调队列优化,当队首的下一位满足条件,则队首pop.
当队尾决策无意义,当且仅当\(sum_{j-1}-g_j<=sum_{k-1}-g_k\)(k在后面,而k比j生效早且k比j小).
这样就可打出正解
后记
任意取出一个能使层数最高的方案,设有CA层,把其中从下往上每一层最大的块编号记为Ai;任取一个能使底边最短的方案,设有CB层,把其中从下往上每一层最大的块编号记为Bi。显然A1>=B1,ACB<=BCB,这说明至少存在一个k属于(1,CB),满足Ak-1>=Bk-1且Ak<=Bk。也就是说,方案 A 第K 层完全被方案 B 第K 层包含。构造一个新方案,第K 层往上按方案 A,往下按方案 B,两边都不要的块放中间当第K 层。新方案的层数与 A 相同,而底边长度与 B 相同。证毕。
这个是一个大佬的证明,我反正没看懂能有其它证法或者可以解释大佬在说什么的神犇,请积极留言.
我的证明偏暴力模拟,希望能够得到更好的宏观理解.
#include<bits/stdc++.h>
#define ll long long
#define lc tree[rt].lc
#define rc tree[rt].rc
#define pa pair<int,int>
#define R register
#define qr qr()
using namespace std;
const int N=2e6+200,MN=5000;
int n,num[N],f[N],sum[N],g[N],q[N];
inline int qr
{
int x=0;bool f=0;char ch=getchar();
while(ch>57||ch<48)
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch>=48&&ch<=57)x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return f?-x:x;
}
void init()
{
n=qr;
for(int i=1;i<=n;++i)
num[i]=qr,sum[i]=sum[i-1]+num[i];
f[n]=1,g[n]=num[n];
int l=1,r=1;
q[l]=n+1;
for(int i=n;i;--i)
{
while(l<r&&sum[q[l+1]-1]-g[q[l+1]]>=sum[i-1])++l;
f[i]=f[q[l]]+1;
g[i]=sum[q[l]-1]-sum[i-1];
while(l<r&&sum[q[r]-1]-g[q[r]]<=sum[i-1]-g[i])--r;
q[++r]=i;
}
printf("%d",f[1]);
}
int main()
{
freopen("c.in","r",stdin);
freopen("c.out","w",stdout);
#ifndef ONLINE_JUDGE
freopen("in.in","r",stdin);
freopen("out.out","w",stdout);
#endif
init();
return 0;
}
/*pu-tao↑zher↑↓
8
18
18
18
12
3
3
4
12
*/



 浙公网安备 33010602011771号
浙公网安备 33010602011771号