列队春游|概率期望|题解
题面
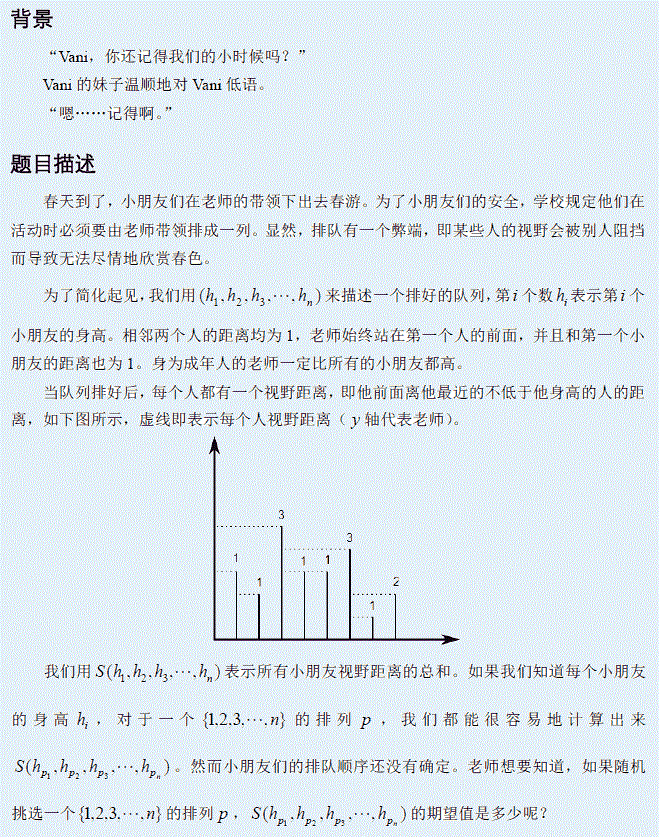



解析
前言,此处所述为\(O(n^2)\)算法,暂时未推出\(O(n)\)的算法,后续可能会更新。
题意非常明白,不多赘述。
我们去考虑单个位置的概率,维护每个人放在该位置对该位置期望的贡献。
以这个思想作为切入点,我们思考,对于一个序列来说,如果它的长度是定的。
设总人数为n,当前我们考虑的人是now,身高用h[]表示,小于等于他身高的人数用ti[]维护。
我们要维护某一个人的视野严格扩展到len的概率&&期望,毕竟我们是要去算对应点的期望的,若概率为PP[],期望为E[]。
用ed[]去存储这个人最长的视野(=1+ti[h[now]-1]).
则\(E[now][len]=len×PP[now][len]\)
在这个时候也可以知道,我们这个人now搁在某个点i处时,当其左侧人数大于等于比其矮的人数,设该点期望为F[].
则\(F[i]=Σ^{now=1}_ {n}(len/n×Σ_{ti[h[now]]}^{len=1}E[now][len])\)
对于一个人now,它能够看到前方视野长为>=len时,概率为P[]。
则\(P[now][len]=A_{ti[h[now]-1]}^{len=1} /A_n^{len}\)
为什么要这个式子,思考在我们把这个人放到某个位置上时,如果他左边的人数k小于等于比这个人小的人的数量。
那么这时我们只用让这些在他左侧的人比他小就好,也就是说,我们这个时候计算长度==k的概率,他是等于我们上面的这个P[]的(因为剩余位不必考虑,不用拿一个比他高的人管住边界)
所以这个P就可以用来处理部分边界问题,上面那个E的表达式就可以通过这个去扩展。
\((ti[h[now]]>=len)E[now][len]=len×PP[now][len]\)
\((ti[h[now]]<len)E[now][len]=len×P[now][len]\)
现在所有东西的未知量只剩下PP[],考虑到这个视野情况事件组内部互斥。
所以\(PP[now][len]=P[now][len]-P[now][len+1]\)
(注:这个式子是自己后面推出来的,还有一种表达方式是从其定义入手,
\(PP[now][len]=P[now][len]×(n-ti[h[now-1]]-1)/(n-len-1)\),代码中用的是这个)
这样我们可以发现,如果依着这个打法维护好这些量之后,这个算法复杂度是\(O(n^3)\).
(注:三层循环,一层是位置,一层是人,一层是视野范围)
这不太理想,虽然说这个数据范围他是允许实现的。
所以考虑优化,我们思考其实一个人放在不同位置他在不受限制时他提供给一点的期望是固定的。
那么我们可以维护一个类似前缀和的算法,我们考虑用EE[]去维护它。
那么\(EE[now][len]=Σ_{len}^{k=1}E[now][k]\)
但是仔细一想,这样怎么处理他左边人数比他小的情况?那就再来个EEE[]数组维护吧。
\(EEE[now][len]=EE[now][len-1]+P[now][len]×len\)
这样,我们的F[]的转移式子就变成了:
\(F[i]=Σ^{now=1}_ {n}EEE[now][min(ed[now],len)]\)
\(ans=Σ^{i=1}_ {n}F[i]\)
方法比较蠢,但问题确实解决了。
#include<bits/stdc++.h>
#define ll long long
#define qr qr()
#define pa pair<int,int>
#define fr first
#define sc second
#define lc tree[rt].ls
#define rc tree[rt].rs
using namespace std;
const int N=2e5+200;
int n,num[N],tot,head[N],ti[1050],ed[305];
long double f[305],p[305][305],ans,pp[305][305],e[305][305],ee[305][305],eee[305][305];
struct node{
int t,w,nx;
}edge[N];
struct What_can_I_say{
int ls,rs,l,r,mx;
}tree[N<<2];
inline int qr
{
int x=0;char ch=getchar();bool f=0;
while(ch>57||ch<48)
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch<=57&&ch>=48)x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return f?-x:x;
}
void add(int f,int t,int w)
{
edge[++tot]={t,w,head[f]};
head[f]=tot;
}
void init()
{
n=qr;
for(int i=1;i<=n;++i)num[i]=qr,++ti[num[i]];
for(int i=1;i<=1000;++i)ti[i]+=ti[i-1];
for(int now=1;now<=n;++now)ed[now]=1+ti[num[now]-1];
for(int now=1;now<=n;++now)
{
p[now][1]=1;
pp[now][1]=1;
for(int len=2;len<=ed[now];++len)
{
p[now][len]=p[now][len-1]*(ti[num[now]-1]-len+2);
p[now][len]/=(n-1-len+2);
if(n-ed[now])
{
pp[now][len]=p[now][len]*(n-ti[num[now]-1]-1)/(n-len);
pp[now][1]-=pp[now][len];
}
}
for(int len=1;len<=ed[now];++len)
{
e[now][len]=pp[now][len]*len;
if(ed[now]^n)
{
ee[now][len]=ee[now][len-1]+e[now][len];
eee[now][len]=ee[now][len-1]+p[now][len]*len;
}
else eee[now][len]=len,ee[now][len]=len;
}
}
for(int i=2;i<=n;++i)
for(int now=1;now<=n;++now)
f[i]+=eee[now][min(ed[now],i)];
for(int i=2;i<=n;++i)ans+=f[i];
printf("%.2Lf",ans/n+1);
// for(int i=1;i<=n;++i)printf("%.2Lf ",ee[i][1]);
// putchar('\n');
// for(int i=1;i<=n;++i)printf("%.2Lf ",ee[i][2]);
// putchar('\n');
// for(int i=1;i<=n;++i)printf("%.2Lf ",ee[i][3]);
// putchar('\n');
// for(int i=1;i<=n;++i)printf("%.2Lf ",pp[i][1]);
// putchar('\n');
// for(int i=1;i<=n;++i)printf("%.2Lf ",pp[i][2]);
// putchar('\n');
// for(int i=1;i<=n;++i)printf("%.2Lf ",pp[i][3]);
// putchar('\n');
// for(int i=1;i<=n;++i)printf("%.2Lf ",p[i][1]);
// putchar('\n');
// for(int i=1;i<=n;++i)printf("%.2Lf ",p[i][2]);
// putchar('\n');
// for(int i=1;i<=n;++i)printf("%.2Lf ",p[i][3]);
// putchar('\n');
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.in","r",stdin);
freopen("out.out","w",stdout);
#endif
init();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号