蒲公英|分块,强制在线|题解

[Violet] 蒲公英

题目背景

亲爱的哥哥：

你在那个城市里面过得好吗？

我在家里面最近很开心呢。昨天晚上奶奶给我讲了那个叫「绝望」的大坏蛋的故事的说！它把人们的房子和田地搞坏，还有好多小朋友也被它杀掉了。我觉得把那么可怕的怪物召唤出来的那个坏蛋也很坏呢。不过奶奶说他是很难受的时候才做出这样的事的……

最近村子里长出了一大片一大片的蒲公英。一刮风，这些蒲公英就能飘到好远的地方了呢。我觉得要是它们能飘到那个城市里面，让哥哥看看就好了呢！

哥哥你要快点回来哦！

爱你的妹妹 Violet

Azure 读完这封信之后微笑了一下。

“蒲公英吗……”

题目描述

在乡下的小路旁种着许多蒲公英，而我们的问题正是与这些蒲公英有关。

为了简化起见，我们把所有的蒲公英看成一个长度为 \(n\) 的序列 \(\{a_1,a_2..a_n\}\)，其中 \(a_i\) 为一个正整数，表示第 \(i\) 棵蒲公英的种类编号。

而每次询问一个区间 \([l, r]\)，你需要回答区间里出现次数最多的是哪种蒲公英，如果有若干种蒲公英出现次数相同，则输出种类编号最小的那个。

注意，你的算法必须是在线的。

输入格式

第一行有两个整数，分别表示蒲公英的数量 \(n\) 和询问次数 \(m\)。

第二行有 \(n\) 个整数，第 \(i\) 个整数表示第 \(i\) 棵蒲公英的种类 \(a_i\)。

接下来 \(m\) 行，每行两个整数 \(l_0, r_0\)，表示一次询问。输入是加密的，解密方法如下：

令上次询问的结果为 \(x\)（如果这是第一次询问，则 \(x = 0\)），设 \(l=((l_0+x-1)\bmod n) + 1,r=((r_0+x-1) \bmod n) + 1\)。如果 \(l > r\)，则交换 \(l, r\)。
最终的询问区间为计算后的 \([l, r]\)。

输出格式

对于每次询问，输出一行一个整数表示答案。

样例 #1

样例输入 #1

6 3 
1 2 3 2 1 2 
1 5 
3 6 
1 5

样例输出 #1

1 
2 
1

提示

数据规模与约定

• 对于 \(20\%\) 的数据，保证 \(n,m \le 3000\)。
• 对于 \(100\%\) 的数据，保证 \(1\le n \le 40000\)，\(1\le m \le 50000\)，\(1\le a_i \le 10^9\)，\(1 \leq l_0, r_0 \leq n\)。

解析:

这个题让我们找一个区间的最小众数,而且要求强制在线处理.
那么我们思考下我们求众数最暴力的方法是所有区间元素扫一遍.
这种方法最过分时O(n×m)时间复杂度,咱们承受不起.
所以想方法,因为区间大,所以处理时间长,也就是说咱想方法把这个大区间给拆开处理?
那么,对于一个区间我们能不能提前处理出来一部分数据让它帮助咱们省时间呢?
图上分析一下.

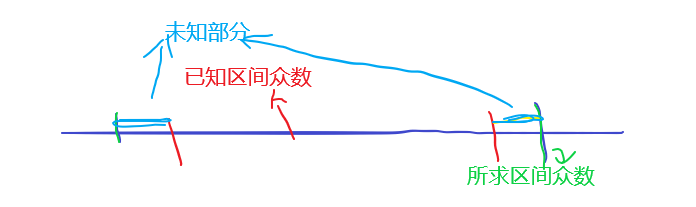
我们要求众数,假设我们已知一个区间的众数(红色),要得到新区间(绿色包含红色区间)众数,答案只可能是已知的众数或者未知部分(蓝色)的某种种类出现次数加已知区间内该种类出现的次数>=已知区间众数.
所以说,我们可以试试预处理出部分区间的众数,作为已知部分,在两端区间进行暴力,就是分块呗.
那么算下(查询的)时间复杂度O(m×(2~4)×sqrt(n))->O(m×sqrt(n));
n,m的范围摆在那,可以承受.
当然了,需要咱们离散化,这种类编号范围有点大.
思路比较简单,剩下的就是代码环节了.

update:

当然了,蓝书上有另外一种思路.
就是每个种类建一个vector,将每一个出现该种类的位置下标push进去.
查询(两端区块)时,直接用upper_bound与lower_bound去查找含于当前块中的元素的下标边界,作差得到该种类在该块中总共出现次数.
这样写码量减轻一些(但也减不了多少.).

正解代码:

#include<bits/stdc++.h>
#define qr qr()
#define ll long long 
using namespace std;

const int N=4e4+20,MB=250;
map <int,int> mp,mf;
//        ↓统计每个块对应品种次数   ↓统计两端不完整区块颜色出现次数的暴力sum 
int p,n,m,sum[MB][N],vr[N],bl[N],tmpsum[N],tot,len/*有几个块*/,blsum[MB][N];
//        初始化pri用到,用于统计我们从一块开始到最后访问的所有颜色总和↑(动态更新以省时间,如果用后缀和复杂度为O(n^2),这样是O(sqrt(n)*n)). 
//                                                   可用一维,每走到一个块上整一次memset亦可.但这题给的空间大,大胆开二维就好. 
struct node{
	int vary,sum;
}pri[MB][MB];
struct nd{
	int id,vary;
	bool operator < (const nd &A)const {
		return vary<A.vary;
	}
}nod[N];
//  ↑从某块到另一块的最小众数(品种出现次数),最有可能的候选数. 
inline int qr
{
	char ch=getchar();bool f=1;int ans=0;
//	while(ch==' '||ch=='\n')ch=getchar();//你永远不知道它输入文件里到底有什么暗物质,所以只排除空格和换行不行.
	while(ch>57||ch<48)ch=getchar();//变成这样就可以了.
	if(ch=='-')ch=getchar(),f=0;
	while(ch>=48&&ch<=57)ans=(ans<<1)+(ans<<3)+ch-48,ch=getchar();
	if(f)return ans;
	return ~(ans-1);
}
int ask(int l,int r)
{//我们两端区间的元素出现次数是唯一可以改变中间区间答案的可能性,所以可能出现的种类顶多就sqrt(n)个,这样初始化省时间. 
	for(int i=l;i<=min(r,(bl[l]+1)*p-1);i++)tmpsum[vr[i]]=0;
	if(bl[l]!=bl[r])for(int i=bl[r]*p;i<=r;i++)tmpsum[vr[i]]=0;
	int mx=0,mxv=0;
	for(int i=l;i<=min(r,(bl[l]+1)*p-1);i++)
	{
		if(++tmpsum[vr[i]]>mx)mx=tmpsum[vr[i]],mxv=vr[i];
		if(tmpsum[vr[i]]==mx)mxv=min(mxv,vr[i]);
	}if(bl[l]!=bl[r])
	{
		for(int i=bl[r]*p;i<=r;i++)
		{
			if(++tmpsum[vr[i]]>mx)mx=tmpsum[vr[i]],mxv=vr[i];
			if(tmpsum[vr[i]]==mx)mxv=min(mxv,vr[i]);
		}
	}
	if(bl[l]+1<=bl[r]-1)
	{	mx=pri[bl[l]+1][bl[r]-1].sum,mxv=pri[bl[l]+1][bl[r]-1].vary;
		for(int i=l;i<=(bl[l]+1)*p-1;i++)
		{	int tmp=sum[bl[r]-1][vr[i]]-sum[bl[l]][vr[i]]+tmpsum[vr[i]];
			if(tmp>mx)mx=tmp,mxv=vr[i];
			if(tmp==mx)mxv=min(vr[i],mxv);
		}for(int i=bl[r]*p;i<=r;i++)
		{	int tmp=sum[bl[r]-1][vr[i]]-sum[bl[l]][vr[i]]+tmpsum[vr[i]];
			if(tmp>mx)mx=tmp,mxv=vr[i];
			if(tmp==mx)mxv=min(vr[i],mxv);
		}
	}return mf[mxv];
}
void init()
{
	n=qr;m=qr;
	p=sqrt(n);len=n/p;
	for(int i=1;i<=n;i++)nod[i]={i,qr};
	sort(nod+1,nod+n+1);
	for(int i=1;i<=n;i++)
	{int vary=nod[i].vary;
		if(!mp[vary])mp[vary]=++tot,mf[tot]=vary;
		bl[nod[i].id]=nod[i].id/p;//排序之后不要直接顺手用i.
		vr[nod[i].id]=mp[vary];
	}
	//超级长的初始化. 
	for(int now=1;now<=n;now++)sum[bl[now]][vr[now]]++;
	for(int nb=1;nb<len;nb++)
	{//初始化pri 
		int mx=0,mxv=0; 
		for(int kb=nb;kb<len;kb++)
		{
			for(int i=kb*p;i<(kb+1)*p;i++)
			{//这样一个块一个块取动态更新保证咱们时间复杂度更小(不需要枚举n个颜色了)也就是为什么我们说这个blsum数组是省了时的. 
				if(++blsum[nb][vr[i]]>mx)mx=blsum[nb][vr[i]],mxv=vr[i];
				if(blsum[nb][vr[i]]==mx)mxv=min(vr[i],mxv);//相同次数取编号较小的. 
			}
			pri[nb][kb]={mxv,mx};
		}
	}
	for(int nb=1;nb<len;nb++)for(int i=1;i<=tot;i++)sum[nb][i]+=sum[nb-1][i];//sum初始化,得到某块及其之前某品种数总和. 
	int x=0;
	for(int i=1;i<=m;i++)
	{
		int l=qr,r=qr;
		l=(l+x-1)%n+1,r=(r+x-1)%n+1;
		if(l>r) swap(l,r);
//		printf("[%d,%d]",l,r); 
		x=ask(l,r);
		printf("%d\n",x);
	}
}
int main()
{
//	freopen("Violet.in","r",stdin);
//	freopen("Violet.txt","w",stdout);
	init();
	return 0;
}
/*
10 7 
1 2 3 4 5 6 7 8 9 10
3 10
1 6
1 5 
3 6 
1 5
9 10
10 10
*/