理想的正方形|单调队列|题解
一.题目引入
有一个a×b的整数组成的矩阵,现请你从中找出一个N×N的正方形区域,使得该区域所有数中的最大值和最小值 的差最小。
输入格式
第一行为3个整数,分别表示a,b,n的值第二行至第a+1行每行为b个非负整数,表示矩阵中相应位置上的数。每 行相邻两数之间用一空格分隔.
100%的数据2<=a,b<=1000,n<=a,n<=b,n<=100
输出格式
仅一个整数,为ab矩阵中所有“nn正方形区域中的最大整数和最小整数的差值”的最小值。
样例
样例输入
5 4 2
1 2 5 6
0 17 16 0
16 17 2 1
2 10 2 1
1 2 2 2
样例输出
1
二.思路梳理
咳咳,观前提示,代码部分正确但是比较冗长且写法抽象...见谅
首先还是梳理下思路,我们看这个题首先可以想到用一个暴力,只要把每一个n×n的正方形右下角都跑一遍算出其结果就可以.
但是仔细想想,可以发现我们暴力的时间复杂度是O((a-n)×(b-n)×n×n)≈n^4,而数据范围是不支持我们纯暴力的.
这时候我们就会去想一些其他方法优化,对于区间极值问题,可以用单调队列,线段树进行优化.
但是这是个二维问题,难道用二维线段树?想了想在我不会打太过复杂且查询时间(O(nlogn))不划算的原因下放弃二维线段树.
所以对于我现在的知识量来说,我们只有一种选择,单调队列.
那现在问题就变成了怎么用单调队列去得出一个二维空间的最值.
想想也不难,拿最大值举例,用一个单调递减队列,对每行从第n个点开始进行遍历.
在每行行首时,将前面的n-1个点与队首元素比较,合法就放到队列之中.每行遍历完毕再清空队列(无效点处理未提及,但不可省)
ok很简单奥,直接开码.
然后当我们悬着一颗紧张的心将码完的代码提交,我们会惊喜地发现我们超时了.
嗯,悬着的心终于吊死了.
再想一下也是,我们看看我们的时间复杂度是个什么玩意,每个点几乎都需要被放入再放出队列n次,那我们要走完整个图,就是O(n×a×b)的近似时间复杂度.
嗯...往好处想至少比n^4好了对吧.
我们重新思考下,我们的重复时间消耗主要出在哪里了?
在我们每一行去将其上面的n-1行都放入队列的时间中,也就是我们的时间复杂度O(n×a×b)中的n...
那,如何避免重复计算n遍同一个点呢.
我们把元素放入队列为了什么呢?为了去找一个点对应的正方形中的最值.
就是因为二维的范围才导致重复的计算.那么我们能不能做到把二维的(n×n)范围最值转化为一个一维(n)范围最值的问题呢.
呀哈,有思路了,我们将一个点及其上面的n-1个点的最值都存在新的一个数组mx/mn对应的坐标点里面.
这就变成了我们在这个点对应的一列上做一个单调队列优化的滑动窗口(大小为n的)问题.
图示:
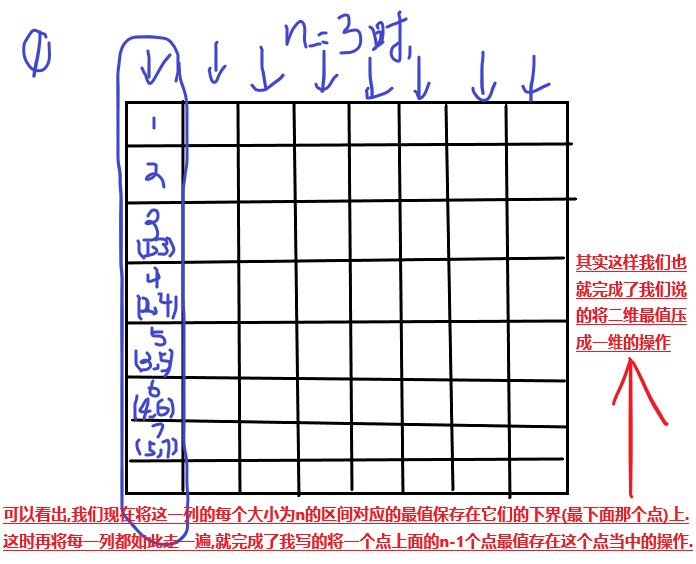
将所有点的y轴向上n范围的最值求出来之后,我们再一行一行的用单调队列将mx/mn所有点的x轴上n范围的点都集中在一点上.
图示:
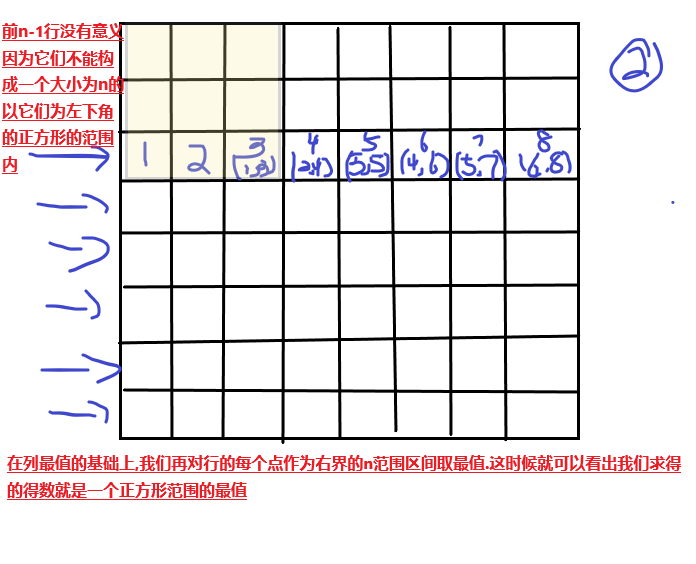
这时求出的就是一个二维区间(n×n)的最值了.具体操作看代码吧.
三.正解代码
点击查看代码
#include<bits/stdc++.h>
#include<deque>
#define ll long long
using namespace std;
struct nd
{
int id;
ll x;
};
deque<nd>qm,qn;
const int N=1e3+20;
int n,x,y;
ll num[N][N],mx[N][N],mn[N][N],ansm[N][N],ansn[N][N],mmn,mmx,ans;
void init()
{
ans=0x7fffffffffffffff;//
// cout<<ans;
scanf("%d%d%d",&x,&y,&n);
for(int i=1;i<=x;i++)
{
for(int j=1;j<=y;j++)
{
scanf("%lld",&num[i][j]);
}
}
}
void rinit(int x)//预处理,前n-1个数都是不可作为矩形统计的,只加入队列,不统计其结果
{
for(int i=1;i<n;i++)
{
while(!qm.empty()&&qm.back().x<=num[x][i])
{
qm.pop_back();
}
if(qm.empty()||qm.back().x>num[x][i])
{
nd d;
d.id=i;
d.x=num[x][i];
qm.push_back(d);
}
while(!qn.empty()&&qn.back().x>=num[x][i])
{
qn.pop_back();
}
if(qn.empty()||qn.back().x<num[x][i])
{
nd d;
d.id=i;
d.x=num[x][i];
qn.push_back(d);
}
}
// ans=min(ans,qm.front().x-qn.front().x);
}
void res()
{
for(int i=1;i<=x;i++)
{
for(int j=n;j<=y;j++)
{
// printf("%d %d\n",i,j);
if(j==n)
{
rinit(i);
}
while(!qm.empty()&&qm.front().id<=j-n)
{
qm.pop_front();
}
while(!qn.empty()&&qn.front().id<=j-n)
{
qn.pop_front();
}
while(!qm.empty()&&qm.back().x<=num[i][j])
{
qm.pop_back();
}
if(qm.empty()||qm.back().x>num[i][j])
{
nd d;
d.id=j;
d.x=num[i][j];
qm.push_back(d);
mx[i][j]=qm.front().x;
}
while(!qn.empty()&&qn.back().x>=num[i][j])
{
qn.pop_back();
}
if(qn.empty()||qn.back().x<num[i][j])
{
nd d;
d.id=j;
d.x=num[i][j];
qn.push_back(d);
mn[i][j]=qn.front().x;
}
}qm.clear(),qn.clear();
}
// for(int i=1;i<=x;i++)
// {
// for(int j=1;j<=y;j++)
// {
// printf("%d ",mx[i][j]);
// }printf("\n");
// } printf("\n");
//
// for(int i=1;i<=x;i++)
// {
// for(int j=1;j<=y;j++)
// {
// printf("%d ",mn[i][j]);
// }printf("\n");
// } printf("\n");
qm.clear(),qn.clear();
for(int j=n;j<=y;j++)
{
for(int i=1;i<=x;i++)
{
if(i<n)//其实等于前面的rinit函数,是用于预处理的
{
// cout<<'#';
while(!qm.empty()&&qm.back().x<=mx[i][j])
{
qm.pop_back();
}
if(qm.empty()||qm.back().x>mx[i][j])
{
nd d;
d.id=i;
d.x=mx[i][j];
qm.push_back(d);
}
while(!qn.empty()&&qn.back().x>=mn[i][j])
{
qn.pop_back();
}
if(qn.empty()||qn.back().x<mn[i][j])
{
nd d;
d.id=i;
d.x=mn[i][j];
qn.push_back(d);
}
continue;
}
// printf("%d %d\n",i,j);
while(!qm.empty()&&qm.front().id<=i-n)
{
qm.pop_front();
}
while(!qn.empty()&&qn.front().id<=i-n)
{
qn.pop_front();
}
while(!qm.empty()&&qm.back().x<=mx[i][j])
{
qm.pop_back();
}
if(qm.empty()||qm.back().x>mx[i][j])
{
nd d;
d.id=i;
d.x=mx[i][j];
qm.push_back(d);
ansm[i][j]=mmx=qm.front().x;
}
while(!qn.empty()&&qn.back().x>=mn[i][j])
{
qn.pop_back();
}
if(qn.empty()||qn.back().x<mn[i][j])
{
nd d;
d.id=i;
d.x=mn[i][j];
qn.push_back(d);
ansn[i][j]=mmn=qn.front().x;
}
if(i>=n)ans=min(ans,mmx-mmn);//,cout<<"("<<i<<","<<j<<")"<<mmx-mmn<<" "<<ans<<endl
}qm.clear(),qn.clear();
// ans=min(ans,mmx-mmn);
}
// for(int i=1;i<=x;i++)
// {
// for(int j=1;j<=y;j++)
// {
// printf("%d ",ansm[i][j]);
// }printf("\n");
// } printf("\n");
//
// for(int i=1;i<=x;i++)
// {
// for(int j=1;j<=y;j++)
// {
// printf("%d ",ansn[i][j]);
// }printf("\n");
// } printf("\n");
printf("%lld",ans);
}
int main()
{
init();
res();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号