LeetCode刷题笔记
前缀和
前缀和主要适⽤的场景是原始数组不会被修改的情况下,频繁查询某个区间的累加和。
class PrefixSum { // 前缀和数组 private int[] prefix; /* 输⼊⼀个数组,构造前缀和 */ public PrefixSum(int[] nums) { prefix = new int[nums.length + 1]; // 计算 nums 的累加和 for (int i = 1; i < prefix.length; i++) { prefix[i] = prefix[i - 1] + nums[i - 1]; } } /* 查询闭区间 [i, j] 的累加和 */ public int query(int i, int j) { return prefix[j + 1] - prefix[i]; } }
差分数组
差分数组的主要适⽤场景是频繁对原始数组的某个区间的元素进⾏增减。
class Difference { //差分数组 private int[] diff; //输入一个初始数组,区间操作在这个数组上进行 public Difference(int[] nums){ diff = new int[nums.length]; diff[0] = nums[0]; for(int i = 1; i < diff.length; i++){ diff[i] = nums[i] - diff[i - 1]; } } //给闭区间 [i, j] 增加 val(可以是负数) public void increment(int i, int j, int val) { diff[i] += val; if(j + 1 < diff.length) diff[j + 1] -= val; } //返回结果数组 public int[] result() { int[] res = new int[diff.length]; res[0] = diff[0]; for(int i = 1; i < res.length; i++){ res[i] = diff[i] + res[i - 1]; } return res; } }
优先级队列(二叉堆)
优先级队列的主要适⽤场景是取最大值或最小值
PriorityQueue<ListNode> pq = new PriorityQueue<>(length, (a, b)->(a.val - b.val));//可以不固定长度,默认小顶堆 pq.add(head); ListNode node = pq.poll(); ListNode node = pq.peek();
快慢指针
快慢指针求单链表的倒数第 k 个节点
ListNode findFromEnd(ListNode head, int k){ ListNode p1 = head; for(int i = 0; i < k; i++){ p1 = p1.next; } ListNode p2 = head; while(p1 != null){ p2 = p2.next; p1 = p1.next; } return p2; }
快慢指针求单链表中点
ListNode middleNode(ListNode head) { ListNode slow = head, fast = head; while (fast != null && fast.next != null){ slow = slow.next; fast = fast.next.next; } return slow; }
快慢指针实现数组原地去重
int removeDuplicates(int[] nums) { if (nums.length == 0) return 0; int slow = 0, fast = 0; while (fast < nums.length) { if (nums[fast] != nums[slow]) { slow++; // 维护 nums[0..slow] ⽆重复 nums[slow] = nums[fast]; } fast++; } // 数组⻓度为索引 + 1 return slow + 1; }
左右指针
从中⼼向两端扩散的 双指针 实现 寻找最大回文子串
public String longestPalindrome(String s) { String res = ""; for(int i = 0; i < s.length(); i++){ String s1 = palindrome(s,i,i); String s2 = palindrome(s,i,i+1); res = res.length() > s1.length() ? res : s1; res = res.length() > s2.length() ? res : s2; } return res; } String palindrome(String s, int l, int r){ while(l >=0 && r < s.length() && s.charAt(l) == s.charAt(r)){ l--; r++; } return s.substring(l + 1,r); }
二分查找
二分查找是从两端向中⼼聚拢的双指针,二分查找通常用于在有序序列定位目标
int binarySearch(int[] nums, int target) {
// ⼀左⼀右两个指针相向⽽⾏
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = (right + left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid - 1;
}
return -1;
}
二分查找更常用的是「搜索左侧边界」和「搜索右侧边界」这两种场景,很少有让你单独「搜索⼀个元素」
// 搜索左侧边界 int left_bound(int[] nums, int target) { if (nums.length == 0) return -1; int left = 0, right = nums.length; while (left < right) { int mid = left + (right - left) / 2; if (nums[mid] == target) { // 当找到 target 时,收缩右侧边界 right = mid; } else if (nums[mid] < target) { left = mid + 1; } else if (nums[mid] > target) { right = mid; } } return left; }
// 搜索右侧边界 int right_bound(int[] nums, int target) { if (nums.length == 0) return -1; int left = 0, right = nums.length; while (left < right) { int mid = left + (right - left) / 2; if (nums[mid] == target) { // 当找到 target 时,收缩左侧边界 left = mid + 1; } else if (nums[mid] < target) { left = mid + 1; } else if (nums[mid] > target) { right = mid; } } return left - 1; }
二分查找还可以抽象成「 满⾜ f(x) == target 的 x (的最⼩值/最大值),f(x)单调递增/递减 ]
// 函数 f 是关于⾃变量 x 的单调函数 int f(int x) { // ... } // 主函数,在 f(x) == target 的约束下求 x 的最值 int solution(int[] nums, int target) { if (nums.length == 0) return -1; // 问⾃⼰:⾃变量 x 的最⼩值是多少? int left = ...; // 问⾃⼰:⾃变量 x 的最⼤值是多少? int right = ... + 1; while (left < right) { int mid = left + (right - left) / 2; if (f(mid) == target) { // 问⾃⼰:题⽬是求左边界还是右边界? // ... } else if (f(mid) < target) { // 问⾃⼰:怎么让 f(x) ⼤⼀点? // ... } else if (f(mid) > target) { // 问⾃⼰:怎么让 f(x) ⼩⼀点? // ... } } return left; }
滑动窗口
可以通过窗口滑动匹配符合条件的字符串
/* 滑动窗⼝算法框架 */ public boolean checkInclusion(String s1, String s2) { Map<Character, Integer> need = new HashMap<Character, Integer>(); Map<Character, Integer> window = new HashMap<Character, Integer>(); for (char c : s1.toCharArray()){ need.put(c,need.getOrDefault(c, 0) + 1); } int left = 0, right = 0; //满足need条件的字符的个数,如果valid和need.size的大小相同,则说明窗口满足条件 int valid = 0; char[] s_c = s2.toCharArray(); while(right < s2.length()){ // c 是将移⼊窗⼝的字符 char c = s_c[right]; // 增⼤窗⼝ right++; // 进⾏窗⼝内数据的⼀系列更新 if(need.containsKey(c)) { window.put(c,window.getOrDefault(c, 0) + 1); if(window.get(c).equals(need.get(c))) valid++; } // 判断左侧窗⼝是否要收缩 while(right - left >= s1.length()){ // 在这⾥判断是否找到了合法的⼦串 if(valid == need.size()) return true; //d 是将移出窗⼝的字符 char d = s_c[left]; //缩⼩窗⼝ left++; // 进⾏窗⼝内数据的⼀系列更新 if(need.containsKey(d)) { if(window.get(d).equals(need.get(d))) valid--; window.put(d,window.getOrDefault(d, 0) - 1); } } } // 未找到符合条件的⼦串 return false; }
递归
不要跳进递归,⽽是利⽤明确的定义来实现 算法逻辑
以反转链表为例,
reverse(head)的定义是反转以head为头的链表后返回反转后的头节点
而reverse(head.next)能反转以head.next为头的链表后返回反转后的头节点,即返回最后一个元素
此时head的next仍然是第二个元素,而第二个元素反转后next为null
所以需要让第二个元素指向head,head指向null才能反转整个链表
还有递归结束条件为 链表为空,返回空;链表只有一个元素,返回这个元素
ListNode reverse(ListNode head) { if (head == null || head.next == null) { return head; } ListNode last = reverse(head.next); head.next.next = head; head.next = null; return last; }
栈
栈主要⽤在括号类的问题。
当问题只需要关注栈的大小时,使用一个变量即栈的大小,进行加减就能模拟入栈出栈。
Stack<Character> stack = new Stack<Character>(); stack.push(c); stack.pop();
stack.peep(c);
stack.empty();
模拟计算器
使用栈模拟计算机
class Solution {
public int calculate(String s) {
Stack<Integer> stack = new Stack<>();
int num = 0;
int pre = 0;
char sign = '+';
for(int i = 0; i < s.length(); i++){
char c = s.charAt(i);
if(Character.isDigit(c)){
num = num * 10 + (c - '0');
}
if(c == '('){
int j = findClosing(s.substring(i));
num = calculate(s.substring(i + 1, i + j));
i += j;
}
if(!Character.isDigit(c) && c != ' ' || i == s.length() - 1){
switch(sign){
case '+':
stack.push(num);
break;
case '-':
stack.push(-num);
break;
case '*':
stack.push(stack.pop() * num);
break;
case '/':
stack.push(stack.pop() / num);
break;
}
sign = c;
num = 0;
}
}
int res = 0;
while(!stack.isEmpty()) res += stack.pop();
return res;
}
//返回右括号的位置
private int findClosing(String s) {
int count = 0;
for(int i = 0; i < s.length(); i++){
if(s.charAt(i) == '(') count++;
else if(s.charAt(i) == ')'){
count--;
if(count == 0) return i;
}else continue;
}
return -1;
}
}
单调栈
单调栈⽤途不太⼴泛,只处理⼀种典型的问题,叫做 Next Greater Element。
比如:给你⼀个数组 nums,请你返回⼀个等⻓的结果数组,结果数组中对应索引存储着下⼀个更⼤元素,如果没有 更⼤的元素,就存 -1。
如果遇到循环数组,可以把数组长度翻倍,然后通过取模拿到循环数组的值
int[] nextGreaterElement(int[] nums){ int[] res = new int[nums.length]; Stack<Integer> stack = new Stack<Integer>(); for(int i = nums.length - 1; i >= 0; i--){ while(!stack.empty()&&stack.peek() <= nums[i]){ stack.pop(); } res[i] = stack.empty()?-1:stack.peek(); stack.push(nums[i]); } return res; }
单调队列
单调队列 可以解决 滑动窗⼝ 取 最大/最小值 相关的问题
MonotonicQueue queue = new MonotonicQueue(); // 在队尾添加元素 n queue.push(n); // 返回当前队列中的最⼤值 queue.max(); // 队头元素如果是 n,删除它 queue.pop(n);
/* 单调队列的实现 */ class MonotonicQueue { LinkedList<Integer> q = new LinkedList<>(); public void push(int n) { // 将⼩于 n 的元素全部删除 while (!q.isEmpty() && q.getLast() < n) { q.pollLast(); } // 然后将 n 加⼊尾部 q.addLast(n); } public int max() { return q.getFirst(); } public void pop(int n) { if (n == q.getFirst()) { q.pollFirst(); } } }
LinkedHashMap
HashMap和双向链表合二为一即是LinkedHashMap,可以用来实现LRU缓存
可以使用Map的方法,使用迭代器遍历有序(插入顺序)
Map<Integer, Integer> cache = new LinkedHashMap<>();
LinkedHashSet
HashSet和双向链表合二为一即是LinkedHashMap,可以用来实现LFU缓存
可以使用Set的方法,使用迭代器遍历有序(插入顺序)
Set<Integer> cache = new LinkedHashSet<>();
随机等概率取元素
如果想⾼效地,等概率地随机获取元素,就要使⽤数组作为底层容器。
如果要保持数组元素的紧凑性,可以把待删除元素换到最后,然后 pop 掉末尾的元素,这样时间复杂度 就是 O(1) 了。当然,我们需要额外的哈希表记录值到索引的映射。
class RandomizedSet { ArrayList<Integer> nums; HashMap<Integer,Integer> valToIndex; Random random; public RandomizedSet() { nums = new ArrayList<>(); valToIndex = new HashMap<>(); random = new Random(); } public boolean insert(int val) { if(valToIndex.containsKey(val)) return false; valToIndex.put(val,nums.size()); nums.add(val); return true; } public boolean remove(int val) { if(!valToIndex.containsKey(val)) return false; int index = valToIndex.get(val); int last = nums.get(nums.size()-1); nums.set(index,last); nums.remove(nums.size()-1); valToIndex.put(last,index); valToIndex.remove(val); return true; } public int getRandom() { return nums.get(random.nextInt(nums.size())); } }
求中位数
两个优先级队列,一个大顶堆,一个小顶堆
class MedianFinder { private PriorityQueue<Integer> large; private PriorityQueue<Integer> small; public MedianFinder() { large = new PriorityQueue<>(); small = new PriorityQueue<>((a,b)->{return b - a;}); } public void addNum(int num) { if(small.size() >= large.size()){ small.offer(num); large.offer(small.poll()); }else{ large.offer(num); small.offer(large.poll()); } } public double findMedian() { if(large.size() < small.size()) return small.peek(); else if(large.size() > small.size()) return large.peek(); return (small.peek() + large.peek())/2.0; } }
二叉树两种解题思路
遍历二叉树计算答案
class Solution { int res = 0; int depth = 0; public int maxDepth(TreeNode root) { traverse(root); return res; } void traverse(TreeNode root){ if(root == null){ res = Math.max(res,depth); return; } depth++; traverse(root.left); traverse(root.right); depth--; } }
分解问题计算答案
class Solution { public int maxDepth(TreeNode root) { if(root == null) return 0; int leftMax = maxDepth(root.left); int rightMax = maxDepth(root.right); int res = Math.max(leftMax,rightMax) + 1; return res; } }
二叉树前序遍历
前序位置的代码在刚刚进⼊⼀个⼆叉树节点的时候执⾏;
前序位置的代码只能从函数参数中获取⽗节点传递来的数据
class Solution { List<Integer> list = new ArrayList<>(); public List<Integer> preorderTraversal(TreeNode root) { traverse(root); return list; } void traverse(TreeNode root){ if(root == null) return; list.add(root.val); traverse(root.left); traverse(root.right); } }
二叉树后序遍历
后序位置的代码在将要离开⼀个⼆叉树节点的时候执⾏;
后序位置的代码 不仅可以获取参数数据,还可以获取到⼦树通过函数返回值传递回来的数据。
//二叉树最大直径 class Solution { int maxDiameter = 0; public int diameterOfBinaryTree(TreeNode root) { maxDepth(root); return maxDiameter; } int maxDepth(TreeNode root){ if(root == null) return 0; int leftMax = maxDepth(root.left); int rightMax = maxDepth(root.right); maxDiameter = Math.max(maxDiameter,leftMax + rightMax); return 1 + Math.max(leftMax, rightMax); } }
如果需要的信息很多,可以考虑用后续遍历,将所有信息作为返回值
class Solution { int maxSum = 0; public int maxSumBST(TreeNode root) { traverse(root); return maxSum; } int[] traverse(TreeNode root){ if(root == null){ return new int[]{1, Integer.MAX_VALUE, Integer.MIN_VALUE, 0}; } int[] left = traverse(root.left); int[] right = traverse(root.right); int[] res = new int[4]; if(left[0] == 1 && right[0] == 1 && root.val > left[2] && root.val < right[1]){ res[0] = 1; res[1] = Math.min(left[1], root.val); res[2] = Math.max(right[1], root.val); res[3] = left[3] + left[3] + root.val; maxSum = Math.max(maxSum, res[3]); }else{ res[0] = 0; } return res; } }
二叉树中序遍历
中序位置的代码在⼀个⼆叉树节点左⼦树都遍历完,即将开始遍历右⼦树的时候执⾏
BST二叉搜索树
1、左⼩右⼤,即每个节点的左⼦树都⽐当前节点的值⼩,右⼦树都⽐当前节点的值⼤。 2、中序遍历结果是有序的。
通过特性找到 二叉搜索树中第K小的元素
class Solution { public int kthSmallest(TreeNode root, int k) { traverse(root, k); return res; } int res = 0; int rank = 0; void traverse(TreeNode root, int k){ if(root == null) return; traverse(root.left, k); rank++; if(k == rank){ res = root.val; return; } traverse(root.right, k); } }
BST 相关的问题,要么利⽤中序遍历的特性满⾜题⽬的要求,要么利⽤ BST 左⼩右⼤的特性提升算法效率
(如果当前节点会对下⾯的⼦节点有整体影响,可以通过辅助函数增⻓参数列表,借助参数传递信息。)
void BST(TreeNode root, int target) { if (root.val == target) // 找到⽬标,做点什么 if (root.val < target) BST(root.right, target); if (root.val > target) BST(root.left, target); }
二叉树层次遍历
⼆叉树主要递归思维的,⽽层序遍历属于迭代遍历
// 输⼊⼀棵⼆叉树的根节点,层序遍历这棵⼆叉树
void levelTraverse(TreeNode root) {
if (root == null) return;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
// 从上到下遍历⼆叉树的每⼀层
while (!q.isEmpty()) {
int sz = q.size();
// 从左到右遍历每⼀层的每个节点
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
// 将下⼀层节点放⼊队列
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}
}
归并排序
归并排序就是⼆叉树的后序遍历
class Merge { private static int[] temp; public static void sort(int[] nums) { temp = new int[nums.length]; sort(nums, 0, nums.length - 1); } private static void sort(int[] nums, int lo, int hi) { if(lo == hi) return; int mid = lo + (hi - lo) / 2; sort(nums, lo, mid); sort(nums, mid + 1, hi); merge(nums, lo, mid, hi); } private static void merge(int[] nums, int lo, int mid, int hi) { for(int i = lo; i <= hi; i++){ temp[i] = nums[i]; } int i = lo, j = mid + 1; for(int p = lo; p <= hi; p++){ if(i == mid + 1) nums[p] = temp[j++]; else if(j == hi + 1) nums[p] = temp[i++]; else if(temp[i] > temp[j]) nums[p] = temp[j++]; else nums[p] = temp[i++]; } } }
快速排序
快速排序就是⼆叉树的前序遍历
你可以这样理解:快速排序的过程是一个构造二叉搜索树的过程
class Quick{ public static void sort(int[] nums){ shuffle(nums); sort(nums, 0, nums.length - 1); } private static void sort(int[] nums, int lo, int hi){ if(lo >= hi) return; int p = partition(nums, lo, hi); sort(nums, lo, p - 1); sort(nums, p + 1, hi); } private static int partition(int[] nums, int lo, int hi){ int pivot = nums[lo]; int i = lo + 1, j = hi; while(i <= j){ while(i < hi && nums[i] <= pivot) i++; while(j > lo && nums[j] > pivot) j--; if(i >= j) break; swap(nums, i, j); } swap(nums, lo, j); return j; } private static void shuffle(int[] nums) { Random rand = new Random(); int n = nums.length; for (int i = 0 ; i < n; i++) { int r = i + rand.nextInt(n - i); swap(nums, i, r); } } private static void swap(int[] nums, int i, int j) { int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; } }
图
图常用的是邻接表和邻接矩阵来实现
// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;
// 邻接矩阵
// matrix[x][y] 记录 x 是否有⼀条指向 y 的边
boolean[][] matrix;
图的遍历(DFS)
多叉树的遍历
/* 多叉树遍历框架 */ void traverse(TreeNode root) { if (root == null) return; for (TreeNode child : root.children) { traverse(child); } }
图的遍历(DFS)可能包含环,就要⼀个 visited 数组进⾏辅助
// 记录被遍历过的节点 boolean[] visited; // 记录从起点到当前节点的路径,可以用来进行环检测 boolean[] onPath; /* 图遍历框架 */ void traverse(Graph graph, int s) { if (visited[s]) return; // 经过节点 s,标记为已遍历 visited[s] = true; // 做选择:标记节点 s 在路径上 onPath[s] = true; for (int neighbor : graph.neighbors(s)) { traverse(graph, neighbor); } // 撤销选择:节点 s 离开路径 onPath[s] = false; }
注意:回溯算法的「做选择」和「撤销选择」在 for 循环⾥⾯,⽽对 onPath 数组的操作在 for 循环 外⾯。
在 for 循环⾥⾯和外⾯唯⼀的区别就是对根节点的处理。
前者会正确打印所有节点的进⼊和离开信息,⽽后者唯独会少打印整棵树根节点的进⼊和离开信息。
为什么回溯算法框架会⽤后者?因为回溯算法关注的不是节点,⽽是树枝。
拓扑排序
直观地说就是,让你把⼀幅图「拉平」,⽽且这个「拉平」的图⾥⾯,所有箭头⽅向都是⼀致的
很显然,如果⼀幅有向图中存在环,是⽆法进⾏拓扑排序的,因为肯定做不到所有箭头⽅向⼀致;反过来, 如果⼀幅图是「有向⽆环图」,那么⼀定可以进⾏拓扑排序
将后序遍历的结果进⾏反转,就是拓扑排序的结果
List<Integer> postorder = new ArrayList<>(); boolean hasCycle = false; boolean[] visited; boolean[] onPath; void traverse(List<Integer>[] graph, int s){ if (onPath[s]) { hasCycle = true; } if (visited[s] || hasCycle) { return; } visited[s] = true; onPath[s] = true; for (int t : graph[s]) { traverse(graph, t); } postorder.add(s); onPath[s] = false; }
图的遍历(BFS)/ 环检测
// 主函数 public boolean canFinish(int numCourses, int[][] prerequisites) { // 建图,有向边代表「被依赖」关系 List<Integer>[] graph = buildGraph(numCourses, prerequisites); // 构建⼊度数组 int[] indegree = new int[numCourses]; for (int[] edge : prerequisites) { int from = edge[1], to = edge[0]; indegree[to]++; } // 根据⼊度初始化队列中的节点 Queue<Integer> q = new LinkedList<>(); for (int i = 0; i < numCourses; i++) { if (indegree[i] == 0) { // 节点 i 没有⼊度,即没有依赖的节点 // 可以作为拓扑排序的起点,加⼊队列 q.offer(i); } } // 记录遍历的节点个数 int count = 0; // 开始执⾏ BFS 循环 while (!q.isEmpty()) { // 弹出节点 cur,并将它指向的节点的⼊度减⼀ int cur = q.poll(); count++; for (int next : graph[cur]) { indegree[next]--; if (indegree[next] == 0) { // 如果⼊度变为 0,说明 next 依赖的节点都已被遍历 q.offer(next); } } } // 如果所有节点都被遍历过,说明不成环 return count == numCourses; } // 建图函数 List<Integer>[] buildGraph(int n, int[][] edges) { List<Integer>[] graph = new LinkedList[numCourses]; for(int i = 0; i < numCourses; i++){ graph[i] = new LinkedList<>(); } for(int[] edge : prerequisites){ int from = edge[1], to = edge[0]; graph[from].add(to); } return graph; }
图的拓扑排序(BFS)
BFS节点的遍历顺序 就是拓扑排序的结果
// 主函数 public int[] findOrder(int numCourses, int[][] prerequisites) { // 建图,和环检测算法相同 List<Integer>[] graph = buildGraph(numCourses, prerequisites); // 计算⼊度,和环检测算法相同 int[] indegree = new int[numCourses]; for (int[] edge : prerequisites) { int from = edge[1], to = edge[0]; indegree[to]++; } // 根据⼊度初始化队列中的节点,和环检测算法相同 Queue<Integer> q = new LinkedList<>(); for (int i = 0; i < numCourses; i++) { if (indegree[i] == 0) { q.offer(i); } } // 记录拓扑排序结果 int[] res = new int[numCourses]; // 记录遍历节点的顺序(索引) int count = 0; // 开始执⾏ BFS 算法 while (!q.isEmpty()) { int cur = q.poll(); // 弹出节点的顺序即为拓扑排序结果 res[count] = cur; count++; for (int next : graph[cur]) { indegree[next]--; if (indegree[next] == 0) { q.offer(next); } } } if (count != numCourses) { // 存在环,拓扑排序不存在 return new int[]{}; } return res; } // 建图函数 List<Integer>[] buildGraph(int n, int[][] edges) { // ⻅前⽂ }
二分图
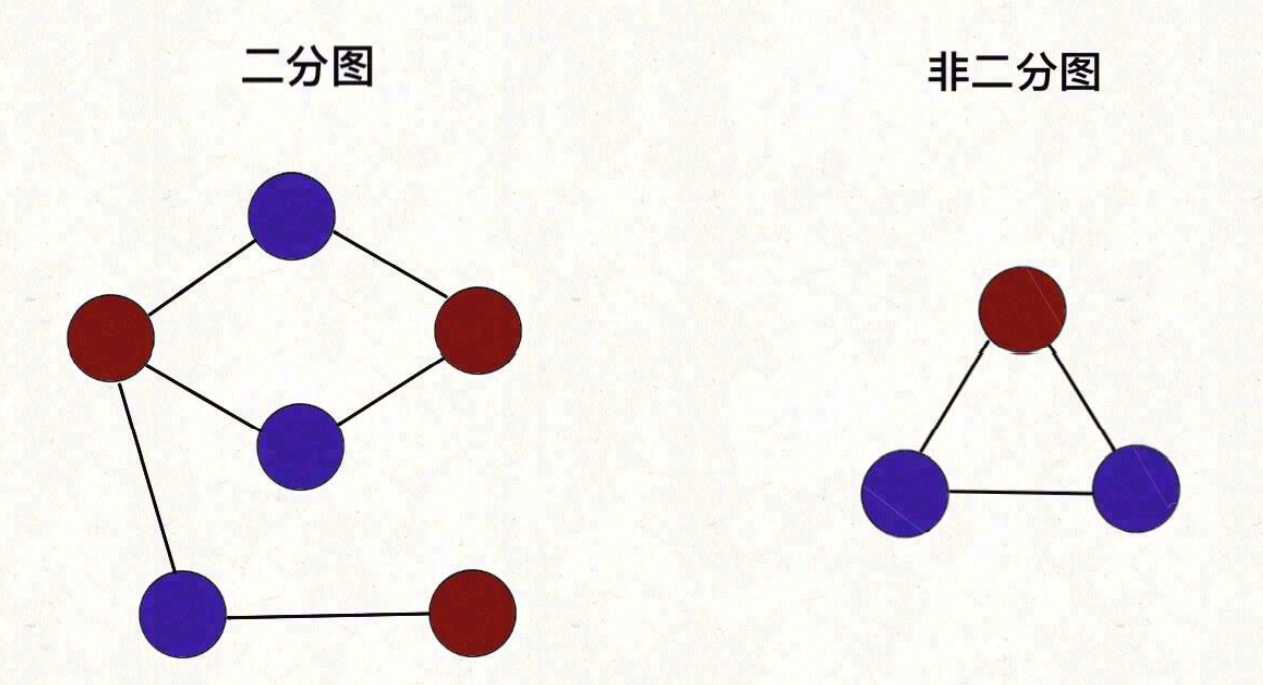
二分图的判定就是「双⾊问题」
遍历⼀遍图,⼀边遍历⼀边染⾊,看看能不能⽤两种颜⾊给所有节点染⾊,且相邻节点的颜⾊都 不相同。
class Solution { private boolean ok = true; private boolean[] color; private boolean[] visited; public boolean isBipartite(int[][] graph) { int n = graph.length; color = new boolean[n]; visited = new boolean[n]; for(int v = 0; v < n; v++){ if(!visited[v]){ traverse(graph, v); } } return ok; } private void traverse(int[][] graph, int v){ if(!ok) return; visited[v] = true; for(int w : graph[v]){ if(!visited[w]){ color[w] = !color[v]; traverse(graph, w); }else{ if(color[w] == color[v]){ ok = false; } } } } }
Union-Find算法
讲 Union-Find 算法,也就是常说的并查集(Disjoint Set)结构,主要是解决图论中「动态连通性」问题的。
class UF{ private int count; private int[] parent; public UF(int n){ this.count = n; parent = new int[n]; for(int i = 0; i < n; i++){ parent[i] = i; } } public void union(int p, int q){ int rootP = find(p); int rootQ = find(q); if(rootP == rootQ) return; parent[rootQ] = rootP; count--; } public boolean connected(int p, int q){ int rootP = find(p); int rootQ = find(q); return rootP == rootQ; } public int find(int x){ if(parent[x] != x){ parent[x] = find(parent[x]); } return parent[x]; } public int count() { return count; } }
Kruskal 最小生成树算法
⼀般来说,我们都是在⽆向加权图中计算最⼩⽣成树的,所以使⽤最⼩⽣成树算法的现实场景 中,图的边权重⼀般代表成本、距离这样的标量。
树的判定算法加上按权重排序的逻辑就变成了 Kruskal 算法
int minimumCost(int n, int[][] connections) { // 城市编号为 1...n,所以初始化大小为 n + 1 UF uf = new UF(n + 1); // 对所有边按照权重从小到大排序 Arrays.sort(connections, (a, b) -> (a[2] - b[2])); // 记录最小生成树的权重之和 int mst = 0; for (int[] edge : connections) { int u = edge[0]; int v = edge[1]; int weight = edge[2]; // 若这条边会产生环,则不能加入 mst if (uf.connected(u, v)) { continue; } // 若这条边不会产生环,则属于最小生成树 mst += weight; uf.union(u, v); } // 保证所有节点都被连通 // 按理说 uf.count() == 1 说明所有节点被连通 // 但因为节点 0 没有被使用,所以 0 会额外占用一个连通分量 return uf.count() == 2 ? mst : -1; } class UF { // 见上文代码实现 }
Prim 最小生成树算法
Prim 算法是从⼀个起点的切分(⼀组横切边)开始执⾏类似 BFS 算法的逻辑,借助切分定理和优先级队列动 态排序的特性,从这个起点「⽣⻓」出⼀棵最⼩⽣成树。
class Prim { // 核⼼数据结构,存储「横切边」的优先级队列 private PriorityQueue<int[]> pq; // 类似 visited 数组的作⽤,记录哪些节点已经成为最⼩⽣成树的⼀部分 private boolean[] inMST; // 记录最⼩⽣成树的权重和 private int weightSum = 0; // graph 是⽤邻接表表示的⼀幅⽆向图, // graph[s] 记录节点 s 所有相邻的边, // 三元组 int[]{from, to, weight} 表示⼀条边 private List<int[]>[] graph; public Prim(List<int[]>[] graph) { this.graph = graph; this.pq = new PriorityQueue<>a((a, b) -> { // 按照边的权重从⼩到⼤排序 return a[2] - b[2]; }); // 图中有 n 个节点 int n = graph.length; this.inMST = new boolean[n]; // 随便从⼀个点开始切分都可以,我们不妨从节点 0 开始 inMST[0] = true; cut(0); // 不断进⾏切分,向最⼩⽣成树中添加边 while (!pq.isEmpty()) { int[] edge = pq.poll(); int to = edge[1]; int weight = edge[2]; if (inMST[to]) { // 节点 to 已经在最⼩⽣成树中,跳过 // 否则这条边会产⽣环 continue; } // 将边 edge 加⼊最⼩⽣成树 weightSum += weight; inMST[to] = true; // 节点 to 加⼊后,进⾏新⼀轮切分,会产⽣更多横切边 cut(to); } } // 将 s 的横切边加⼊优先队列 private void cut(int s) { // 遍历 s 的邻边 for (int[] edge : graph[s]) { int to = edge[1]; if (inMST[to]) { // 相邻接点 to 已经在最⼩⽣成树中,跳过 // 否则这条边会产⽣环 continue; } // 加⼊横切边队列 pq.offer(edge); } } // 最⼩⽣成树的权重和 public int weightSum() { return weightSum; } // 判断最⼩⽣成树是否包含图中的所有节点 public boolean allConnected() { for (int i = 0; i < inMST.length; i++) { if (!inMST[i]) { return false; } } return true; } }
Dijkstra 算法
Dijkstra 算法就是⼀个 BFS 算法使用贪心算法的加强版,返回从起点 start 到所有其他节点的最短路径
class State { // 图节点的 id int id; // 从 start 节点到当前节点的距离 int distFromStart; State(int id, int distFromStart) { this.id = id; this.distFromStart = distFromStart; } } // 返回节点 from 到节点 to 之间的边的权重 int weight(int from, int to); // 输⼊节点 s 返回 s 的相邻节点 List<Integer> adj(int s); // 输⼊⼀幅图和⼀个起点 start,计算 start 到其他节点的最短距离 int[] dijkstra(int start, List<Integer>[] graph){ // 图中节点的个数 int V = graph.length; // 定义:distTo[i] 的值就是节点 start 到达节点 i 的最短路径权重 int[] distTo = new int[V]; // 求最⼩值,所以初始化为正⽆穷 Arrays.fill(disTo,Integer.MAX_VALUE); //start 到 start 的最短距离就是 0 distTo[start] = 0; // 优先级队列,distFromStart 较⼩的排在前⾯,贪⼼算法 Queue<State> pq = new PriorityQueue<>((a, b) -> {return a.distFromStart - b.distFromStart;}); // 从起点 start 开始进⾏ BFS pq.offer(new State(start, 0)); while(!pq.isEmpty()){
//弹出来的最小值有两种可能:一是到达某个节点最短距离的状态对象;二是已经弹出的节点之前的状态对象 State curState = pq.poll(); int curNodeID = curState.id; int curDistFromStart = curState.disFromStart; if(curDistFromStart > distTo[curNodeID]){ // 已经有⼀条更短的路径到达 curNode 节点了 continue; } // 将 curNode 的相邻节点装⼊队列 for(int nextNodeID : adj(curNodeID)){ // 给还没遍历的点一个可能的最短距离,给遍历过的点看看能否更新最短距离 int disToNextNode = distTo[curNodeID] + weight(curNodeID, nextNodeID); if(disTo[nextNodeID] > disToNextNode){ distTo[nextNodeID] = distToNextNode; pq.offer(new State(nextNodeID, distToNextNode)); } } } return disTo; }
回溯算法
回溯算法其实就是我们常说的 DFS 算法,本质上就是⼀种暴⼒穷举算法。
在递归调⽤之前「做选择」,在递归调⽤之后「撤销选择」
写 backtrack 函数时,需要维护⾛过的「路径」和当前可以做的「选择列表」,当触发「结束条件」时, 将「路径」记⼊结果集。
排列/组合/⼦集问题的三种形式在代码上的区别:
由于⼦集问题和组合问题本质上是⼀样的,⽆⾮就是 base case 有⼀些区别,所以把这两个问题放在⼀起看。
1)元素⽆重不可复选
/* 组合/⼦集问题回溯算法框架 */ void backtrack(int[] nums, int start) { // 回溯算法标准框架 for (int i = start; i < nums.length; i++) { // 做选择 track.addLast(nums[i]); // 注意参数 backtrack(nums, i + 1); // 撤销选择 track.removeLast(); } } /* 排列问题回溯算法框架 */ void backtrack(int[] nums) { for (int i = 0; i < nums.length; i++) { // 剪枝逻辑 if (used[i]) { continue; } // 做选择 used[i] = true; track.addLast(nums[i]); backtrack(nums); // 撤销选择 track.removeLast(); used[i] = false; } }
2)元素可重不可复选
Arrays.sort(nums); /* 组合/⼦集问题回溯算法框架 */ void backtrack(int[] nums, int start) { // 回溯算法标准框架 for (int i = start; i < nums.length; i++) { // 剪枝逻辑,跳过值相同的相邻树枝 if (i > start && nums[i] == nums[i - 1]) { continue; } // 做选择 track.addLast(nums[i]); // 注意参数 backtrack(nums, i + 1); // 撤销选择 track.removeLast(); } } Arrays.sort(nums); /* 排列问题回溯算法框架 */ void backtrack(int[] nums) { for (int i = 0; i < nums.length; i++) { // 剪枝逻辑 if (used[i]) { continue; } // 剪枝逻辑,固定相同的元素在排列中的相对位置 if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) { continue; } // 做选择 used[i] = true; track.addLast(nums[i]); backtrack(nums); // 撤销选择 track.removeLast(); used[i] = false; } }
3)元素⽆重可复选
/* 组合/⼦集问题回溯算法框架 */ void backtrack(int[] nums, int start) { // 回溯算法标准框架 for (int i = start; i < nums.length; i++) { // 做选择 track.addLast(nums[i]); // 注意参数 backtrack(nums, i); // 撤销选择 track.removeLast(); } } /* 排列问题回溯算法框架 */ void backtrack(int[] nums) { for (int i = 0; i < nums.length; i++) { // 做选择 track.addLast(nums[i]); backtrack(nums); // 撤销选择 track.removeLast(); } }
位图技巧
int used = 0; used |= 1 << i; // 将第 i 位置为 1 used ^= 1 << i; // 使⽤异或运算将第 i 位恢复 0 int res = (((used >> i) & 1) == 1) // 判断第 i 位是否是 1
岛屿问题
岛屿数量
其他岛屿题一般都是有特殊条件需要先淹了某些岛屿,或者淹岛屿时记录某些信息
class Solution { public int numIslands(char[][] grid) { int res = 0; int m = grid.length, n = grid[0].length; for(int i = 0; i < m; i++){ for(int j = 0; j < n; j++){ if(grid[i][j] == '1'){
// 每发现⼀个岛屿,岛屿数量加⼀ res++;
// 然后使⽤ DFS 将岛屿淹了 dfs(grid, i, j); } } } return res; } void dfs(char[][] grid, int i, int j){ int m = grid.length, n = grid[0].length; if(i < 0 || j < 0 || i >= m || j >= n){ return; } if(grid[i][j] == '0'){ return; } grid[i][j] = '0'; dfs(grid, i + 1, j); dfs(grid, i, j + 1); dfs(grid, i - 1, j); dfs(grid, i, j - 1); } }
BFS
BFS的大多数问题本质上就是⼀幅「图」,让你从⼀个起点,⾛到终点,问最短路径
双向 BFS,可以 进⼀步提⾼算法的效率。从起点和终点同时开始扩散,当两边有交集的时候停⽌。
// 计算从起点 start 到终点 target 的最近距离 int BFS(Node start, Node target) { Queue<Node> q; // 核⼼数据结构 Set<Node> visited; // 避免⾛回头路 q.offer(start); // 将起点加⼊队列 visited.add(start); int step = 0; // 记录扩散的步数 while (q not empty) { int sz = q.size(); /* 将当前队列中的所有节点向四周扩散 */ for (int i = 0; i < sz; i++) { Node cur = q.poll(); /* 划重点:这⾥判断是否到达终点 */ if (cur is target) return step; /* 将 cur 的相邻节点加⼊队列 */ for (Node x : cur.adj()) { if (x not in visited) { q.offer(x); visited.add(x); } } } /* 划重点:更新步数在这⾥ */ step++; } }
动态规划
特点:
1、重叠子问题
2、状态转移方程
3、最优子结构
解题套路:
1、明确状态
2、明确选择
3、明确dp数组定义
4、明确base case
//初始化 base case dp[0][0][...] = base; //穷举 for 状态1 in 状态1的所有取值 for 状态2 in 状态2的所有取值 for ... dp[状态1][状态2][...] = 求最值(选择1,选择2...)
LCS
最长公共子序列
对于两个字符串求子序列的问题,都是用两个指针i和j分别在两个字符串上移动
class Solution { int[][] memo; public int longestCommonSubsequence(String s1, String s2) { int m = s1.length(), n = s2.length(); memo = new int[m][n]; for(int[] row : memo) Arrays.fill(row, -1); return dp(s1, 0, s2, 0); } int dp(String s1, int i, String s2, int j){ if(i == s1.length() || j == s2.length()) return 0; if(memo[i][j] != -1) return memo[i][j]; if(s1.charAt(i) == s2.charAt(j)){ memo[i][j] = 1 + dp(s1, i + 1, s2, j + 1); }else{ memo[i][j] = Math.max( dp(s1, i + 1, s2, j), dp(s1, i, s2, j + 1) ); } return memo[i][j]; } }
自底向上解法
class Solution { public int longestCommonSubsequence(String s1, String s2) { int m = s1.length(), n = s2.length(); int[][] dp = new int[m + 1][n + 1]; for(int i = 1; i <= m; i++){ for(int j = 1; j <= n; j++){ if(s1.charAt(i - 1) == s2.charAt(j - 1)){ dp[i][j] = 1 + dp[i - 1][j - 1]; }else{ dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]); } } } return dp[m][n]; } }
算法时空复杂度
1、只保留增长速率最快的项,其他的项可以省略。
常数因子都可以忽略不计
增长速率慢的项在增长速率快的项面前也可以忽略不计
2、Big O 记号表示复杂度的「上界」
找最坏情况
3、只需要搞清楚代码到底在干什么,就能轻松计算出正确的复杂度了。
非递归算法中嵌套循环很常见,大部分场景下,只需把每一层的复杂度相乘就是总的时间复杂度
但有时候只看嵌套循环的层数并不准确,还得看算法具体在做什么
4、如果想衡量数据结构类中的某个方法的时间复杂度,不能简单地看最坏时间复杂度,而应该看摊还(平均)时间复杂度。
5、递归算法的时间复杂度 = 递归的次数 x 函数本身的时间复杂度
递归算法的时间复杂度 = 递归树的节点个数 x 每个节点的时间复杂度
高度为n的一棵满k叉树,其节点总数为(k^n-1)/(k-1)
6、递归算法的空间复杂度 = 递归堆栈的深度 + 算法申请的存储空间
递归算法的空间复杂度 = 递归树的高度 + 算法申请的存储空间



 浙公网安备 33010602011771号
浙公网安备 33010602011771号