[LeetCode] #110 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。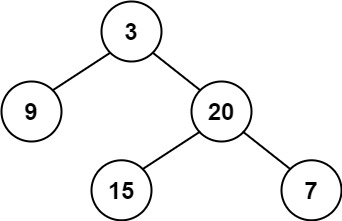

 

 

 

输入：root = [3,9,20,null,null,15,7]

输出：true

可以利用求二叉树高度的函数[LeetCode] #104 二叉树的最大深度

比较每个节点的左右子树的高度差，这是自顶向下的解法，需要遍历每个节点也称暴力解法

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) return true;
        else return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
        }
    }

    public int height(TreeNode root) {
        if (root == null) return 0;
        else return Math.max(height(root.left), height(root.right)) + 1;
    }
}

也可以用自底向上的解法。自底向上递归的做法类似于后序遍历，对于当前遍历到的节点，先递归地判断其左右子树是否平衡，再判断以当前节点为根的子树是否平衡。如果一棵子树是平衡的，则返回其高度（高度一定是非负整数），否则返回−1。如果存在一棵子树不平衡，则整个二叉树一定不平衡。不一定需要遍历全部节点。

class Solution {
    public boolean isBalanced(TreeNode root) {
        return height(root) >= 0;
    }

    public int height(TreeNode root) {
        if (root == null) return 0;
        int leftHeight = height(root.left);
        int rightHeight = height(root.right);
        if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) return -1;
        elsereturn Math.max(leftHeight, rightHeight) + 1;
    }
}

知识点：无

总结：对于判断树结构是否满足要求时，自底向上的解法 时间复杂度 更低。