[LeetCode] #69 x 的平方根

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

输入: 4

输出: 2

从1开始递增，看哪个数的平方等于x。

class Solution {
    public int mySqrt(int x) {
        int i = 1;
        while(x/i >= i){
            i++;
        }
        return i-1;
    }
}

官方解法一：袖珍计算器算法

通过其它的数学函数代替平方根函数得到精确结果，取整数部分作为答案

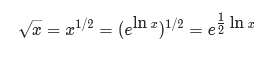
class Solution {
    public int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }
        int ans = (int) Math.exp(0.5 * Math.log(x));
        return (long) (ans + 1) * (ans + 1) <= x ? ans + 1 : ans;
    }
}

官方解法二：二分查找

在0~x中找满足k*k<=x的最大值

class Solution {
    public int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long) mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
}

官方解法三：牛顿迭代

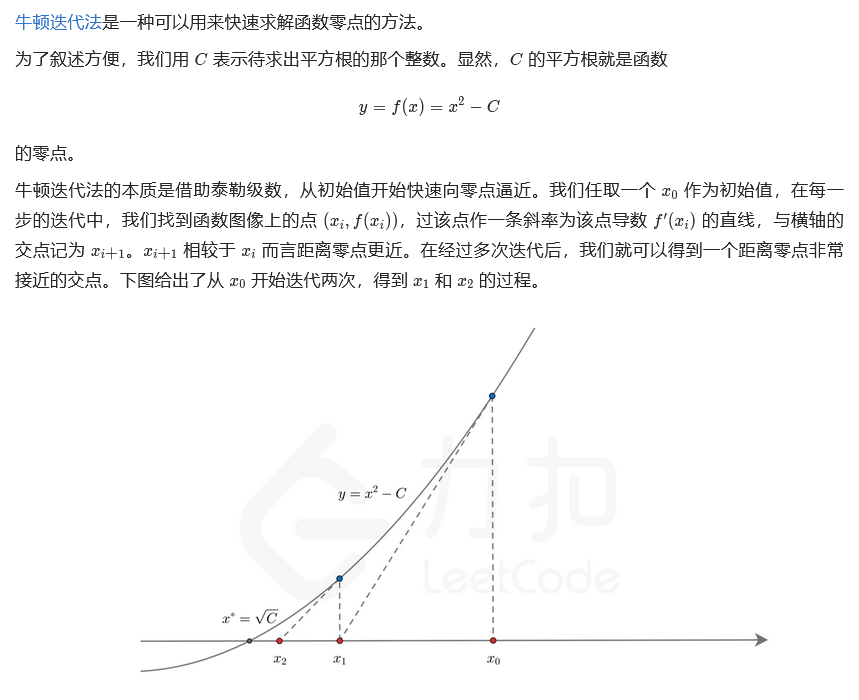
class Solution {
    public int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }

        double C = x, x0 = x;
        while (true) {
            double xi = 0.5 * (x0 + C / x0);
            if (Math.abs(x0 - xi) < 1e-7) {
                break;
            }
            x0 = xi;
        }
        return (int) x0;
    }
}

知识点：

Math.exp()返回自然数底数 e 的参数次方

Math.log()返回值的自然对数（以e为底）

Math.abs()返回绝对值

总结：在一定范围内找一个数可以使用二分法