【转】 分类模型评估指标汇总
作者:努力的孔子
https://www.cnblogs.com/yanshw/p/10735079.html
对模型进行评估时,可以选择很多种指标,但不同的指标可能得到不同的结果,如何选择合适的指标,需要取决于任务需求。
正确率与错误率
正确率:正确分类的样本数/总样本数,accuracy
错误率:错误分类的样本数/总样本数,error
正确率+错误率=1
这两种指标最简单,也最常用
缺点
-
不一定能反应模型的泛化能力,如类别不均衡问题。
-
不能满足所有任务需求
如有一车西瓜,任务一:挑出的好瓜中有多少实际是好瓜,任务二: 所有的好瓜有多少被挑出来了,显然正确率和错误率不能解决这个问题。
查准率与查全率
先认识几个概念
正样本/正元组:目标元组,感兴趣的元组
负样本/负元组:其他元组
对于二分类问题,模型的预测结果可以划分为:真正例 TP、假正例 FP、真负例 TN、 假负例 FN,
真正例就是实际为正、预测为正,其他同理
显然 TP+FP+TN+FN=总样本数
混淆矩阵
把上面四种划分用混淆矩阵来表示
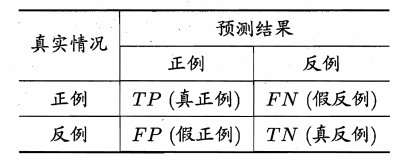
从而得出如下概念
查准率:预测为正里多少实际为正,precision,也叫精度
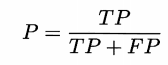
查全率:实际为正里多少预测为正,recall,也叫召回率
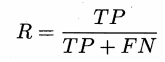
查准率和查全率是一对矛盾的度量。通常来讲,查准率高,查全率就低,反之亦然。
例如还是一车西瓜,我希望将所有好瓜尽可能选出来,如果我把所有瓜都选了,那自然所有好瓜都被选了,这就需要所有的瓜被识别为好瓜,此时查准率较低,而召回率是100%,
如果我希望选出的瓜都是好瓜,那就要慎重了,宁可不选,不能错选,这就需要预测为正就必须是真正例,此时查准率是100%,查全率可能较低。
注意我说的是可能较低,通常如果样本很好分,比如正的全分到正的,负的全分到负的,那查准率、查全率都是100%,不矛盾。
P-R曲线
既然矛盾,那两者之间的关系应该如下图
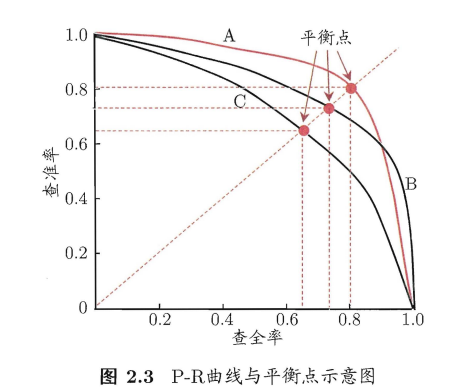
这条曲线叫 P-R曲线,即查准率-查全率曲线。
这条曲线怎么画出来的呢?可以这么理解,假如我用某种方法得到样本是正例的概率(如用模型对所有样本进行预测),然后把样本按概率排序,从高到低
如果模型把第一个预测为正,其余预测为负,此时查准率为1,查全率接近于0,
如果模型把前2个预测为正,其余预测为负,此时查准率稍微降低,查全率稍微增加,
依次...
如果模型把除最后一个外的样本预测为正,最后一个预测为负,那么查准率很低,查全率很高。
此时我把数据顺序打乱,画出来的图依然一样,即上图。
既然查准率和查全率互相矛盾,那用哪个作为评价指标呢?或者说同时用两个指标怎么评价模型呢?
两种情形
-
如果学习器A的P-R曲线能完全“包住”学习器C的P-R曲线,则A的性能优于C
-
如果学习器A的P-R曲线与学习器B的P-R曲线相交,则难以判断孰优孰劣,此时通常的作法是,固定查准率,比较查全率,或者固定查全率,比较查准率。
通常情况下曲线会相交,但是人们仍希望把两个学习器比出个高低,一个合理的方式是比较两条P-R曲线下的面积。
但是这个面积不好计算,于是人们又设计了一些其他综合考虑查准率查全率的方式,来替代面积计算。
平衡点:Break-Event Point,简称BEP,就是选择 查准率=查全率 的点,即上图,y=x直线与P-R曲线的交点
这种方法比较暴力
F1 与 Fβ 度量
更常用的方法是F1度量
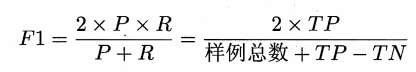
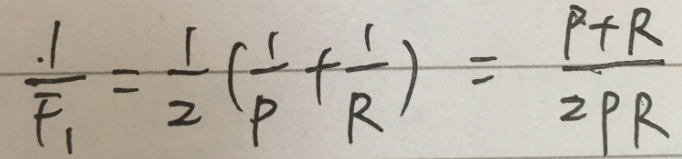
即 F1 是 P 和 R 的调和平均数。
与算数平均数 和 几何平均数相比,调和平均数更重视较小值。
在一些应用中,对查准率和查全率的重视程度有所不同。
例如商品推荐系统,为了避免骚扰客户,希望推荐的内容都是客户感兴趣的,此时查准率比较重要,
又如资料查询系统,为了不漏掉有用信息,希望把所有资料都取到,此时查全率比较重要。
此时需要对查准率和查全率进行加权
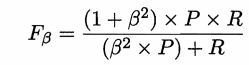

即 P 和 R 的加权调和平均数。
β>0,β度量了查全率对查准率的重要性,β=1时即为F1
β>1,查全率更重要,β<1,查准率更重要
多分类的F1
多分类没有正例负例之说,那么可以转化为多个二分类,即多个混淆矩阵,在这多个混淆矩阵上综合考虑查准率和查全率,即多分类的F1
方法1
直接在每个混淆矩阵上计算出查准率和查全率,再求平均,这样得到“宏查准率”,“宏查全率”和“宏F1”

方法2
把混淆矩阵中对应元素相加求平均,即 TP 的平均,TN 的平均,等,再计算查准率、查全率、F1,这样得到“微查准率”,“微查全率”和“微F1”
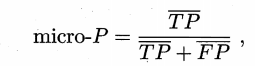
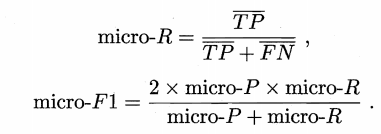
ROC 与 AUC
很多学习器是为样本生成一个概率,然后和设定阈值进行比较,大于阈值为正例,小于为负例,如逻辑回归。
而模型的优劣取决于两点:
-
这个概率的计算准确与否
-
阈值的设定
我们把计算出的概率按从大到小排序,然后在某个点划分开,这个点就是阈值,可以根据实际任务需求来确定这个阈值,比如更重视查准率,则阈值设大点,若更重视查全率,则阈值设小点,
这里体现了同一模型的优化,
不同的模型计算出的概率是不一样的,也就是说样本按概率排序时顺序不同,那切分时自然可能分到不同的类,
这里体现了不同模型之间的差异,
所以ROC可以用来模型优化和模型选择,理论上讲 P-R曲线也可以。
ROC曲线的绘制方法与P-R曲线类似,不再赘述,结果如下图

横坐标为假正例率,纵坐标为真正例率,曲线下的面积叫 AUC
如何评价模型呢?
-
若学习器A的ROC曲线能包住学习器B的ROC曲线,则A优于B
-
若学习器A的ROC曲线与学习器B的ROC曲线相交,则难以比较孰优孰劣,此时可以比较AUC的大小
总结
-
模型评估主要考虑两种场景:类别均衡,类别不均衡
-
模型评估必须考虑实际任务需求
-
P-R 曲线和 ROC曲线可以用于模型选择
-
ROC曲线可以用于模型优化
参考资料:
周志华《机器学习》
本文由博客一文多发平台 OpenWrite 发布!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号