算法图解读书笔记
一、前言
为了解决自己对传说中高大上的算法的好奇之心，特意找了一本算法入门的书籍（算是科普读物）《算法图解》进行研究。
本篇文章是对这本书的一些笔记和精简。·持续更新
二、目录
- 算法简介
- 选择排序
- 递归
- 快速排序
- 散列表
- 广度优先搜索
- 狄克斯特拉算法
- 贪婪算法
- 动态规划
- K最邻近算法
- 拓展
- 答案
三、算法简介
简单查找
本质：列表中逐个比较
简单实现：
def search(target_list,item): for i in target_list: if i == item: return i return None
二分查找
本质：每次取中值与item比较，中值比item大了在左边列表中继续下一轮，相反中值比item小了，在右边列表中继续下一轮取中值。
简单实现：
def binary_search(tlist,item): low = 0 high = len(tlist)-1 while low <= high: mid = int((low + high)/2) if item < tlist[mid]: high = mid-1 elif item >tlist[mid]: low = mid+1 else: return (mid,tlist[mid]) return None
大O表示法
本质：通过执行语句数的数量级来描述程序运行时间，一般以最糟糕的情况下执行的语句数为准，例如简单实现为O(n)，即假定要找的元素在最后一个。忽略数量级前的常数量，如O(5n!)是没必要的，直接写O(n！).
常见时间：
O(1): 常量时间，哈希
O(log2(n)): 对数时间，二分，
O(n): 线性时间，简单
O(nlog2(n)): 快速排序
O(n2): 选择排序（冒泡）
O(n!): 旅行商问题
四、选择排序
数组和链表
数组： 内存中连续存储，随意查询元素， 随机查询快（知道元素index），增删改慢（因为有顺序，有预设内存空间，中间插入或者超出预留内存，就会重新构建）
链表： 内存中分散，每一个元素记录下一个元素位置，随机查询慢（只能从第一个往后推），要全部查询的情况下也不慢，增删改快（分散存储只要更改上一个元素的记录），
选择排序（冒泡排序）
本质：每一次选出最大的或最小的元素，循环排序，O（n2）
简单实现从小到大排序：
def mysort(target_list): new_list = [] while target_list: mini = target_list[0] for i in target_list: if i <= mini: mini = i new_list.append(mini) target_list.remove(mini) return new_list
五、递归
递归与循环
递归优势在于代码更容易理解
循环优势在于性能更高
基线条件和递归条件
基线条件指退出的条件，防止无限递归
递归条件指函数的自我调用
def condition(i): print(i) if i<0: #基线条件，达到就退出递归 return else: condition(i-1) #递归条件，实现递归
栈
本质：后进先出的结构，（同搭积木，先放的在底下，后方在上面，拿永远拿最上面的，也是最后放上去的），有压入弹出两种操作
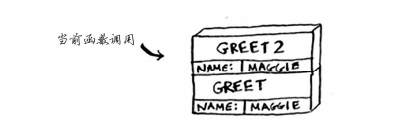
简单例子二：
def test(n): '''阶乘函数''' if n== 1: return 1 else: return n*test(n-1)
注意：递归是有代价的，一次递归就可能创建多个调用栈，当递归未结束，调用栈会越来越高，占用内存会越来越大，直到程序崩溃，Python默认栈高为1000，可以更改。但是更改没有太大意义，更好的办法是修改你的算法。
六、快速排序
分而治之（divide and conquer D&C）
本质：递归分解问题
简单例子：
def mysum(target_list): '''求和函数'''if target_list:return target_list[0]+test(target_list[1:]) else: return 0def mylen(target_list):
'''求长度函数'''
if target_list:
return 1+test(target_list[1:])
else:
return 0
def mymax(target_list):
'''求最大值函数'''
if len(target_list)==2:
return target_list[0] if target_list[0]>=target_list[1] else target_list[1]
sub_max = test(target_list[1:])
return target_list[0] if target_list[0]>=sub_max else sub_max
快速排序
本质：
