机器学习经典算法之KNN

一、前言

KNN 的英文叫 K-Nearest Neighbor，应该算是数据挖掘算法中最简单的一种。

先用一个例子体会下。

/*请尊重作者劳动成果，转载请标明原文链接：*/

/* https://www.cnblogs.com/jpcflyer/p/11111817.html * /

假设，我们想对电影的类型进行分类，统计了电影中打斗次数、接吻次数，当然还有其他的指标也可以被统计到，如下表所示。

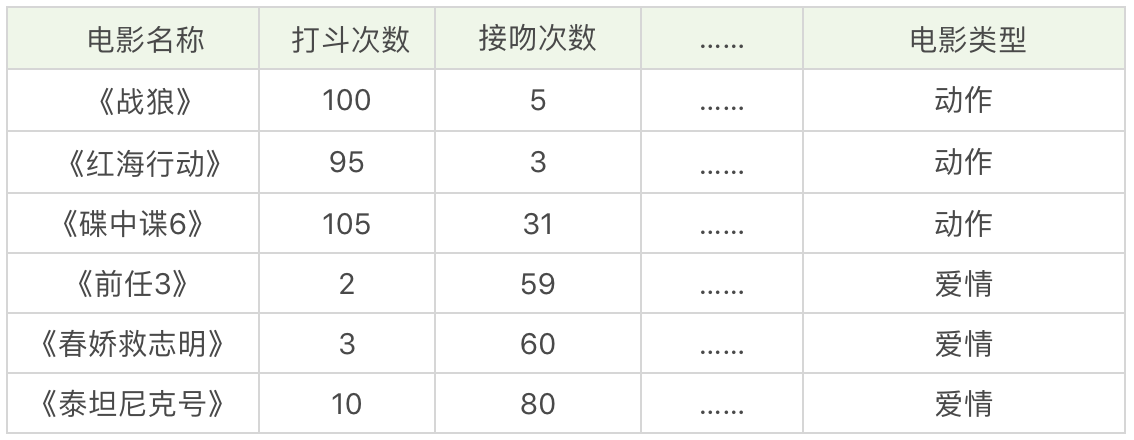
我们很容易理解《战狼》《红海行动》《碟中谍 6》是动作片，《前任 3》《春娇救志明》《泰坦尼克号》是爱情片，但是有没有一种方法让机器也可以掌握这个分类的规则，当有一部新电影的时候，也可以对它的类型自动分类呢？

我们可以把打斗次数看成 X 轴，接吻次数看成 Y 轴，然后在二维的坐标轴上，对这几部电影进行标记，如下图所示。对于未知的电影 A，坐标为 (x,y)，我们需要看下离电影 A 最近的都有哪些电影，这些电影中的大多数属于哪个分类，那么电影 A 就属于哪个分类。实际操作中，我们还需要确定一个 K 值，也就是我们要观察离电影 A 最近的电影有多少个。

 

 

二、KNN 的工作原理

“近朱者赤，近墨者黑”可以说是 KNN 的工作原理。整个计算过程分为三步：

1. 计算待分类物体与其他物体之间的距离；

2. 统计距离最近的 K 个邻居；

3.对于 K 个最近的邻居，它们属于哪个分类最多，待分类物体就属于哪一类。

 

K 值如何选择

你能看出整个 KNN 的分类过程，K 值的选择还是很重要的。那么问题来了，K 值选择多少是适合的呢？

如果 K 值比较小，就相当于未分类物体与它的邻居非常接近才行。这样产生的一个问题就是，如果邻居点是个噪声点，那么未分类物体的分类也会产生误差，这样 KNN 分类就会产生过拟合。

如果 K 值比较大，相当于距离过远的点也会对未知物体的分类产生影响，虽然这种情况的好处是鲁棒性强，但是不足也很明显，会产生欠拟合情况，也就是没有把未分类物体真正分类出来。

所以 K 值应该是个实践出来的结果，并不是我们事先而定的。在工程上，我们一般采用交叉验证的方式选取 K 值。

交叉验证的思路就是，把样本集中的大部分样本作为训练集，剩余的小部分样本用于预测，来验证分类模型的准确性。所以在 KNN 算法中，我们一般会把 K 值选取在较小的范围内，同时在验证集上准确率最高的那一个最终确定作为 K 值。

 

距离如何计算

在 KNN 算法中，还有一个重要的计算就是关于距离的度量。两个样本点之间的距离代表了这两个样本之间的相似度。距离越大，差异性越大；距离越小，相似度越大。

关于距离的计算方式有下面五种方式：

欧氏距离；

曼哈顿距离；

闵可夫斯基距离；

切比雪夫距离；

余弦距离。

其中前三种距离是 KNN 中最常用的距离，现在分别讲解下。

 

欧氏距离是我们最常用的距离公式，也叫做欧几里得距离。在二维空间中，两点的欧式距离就是：

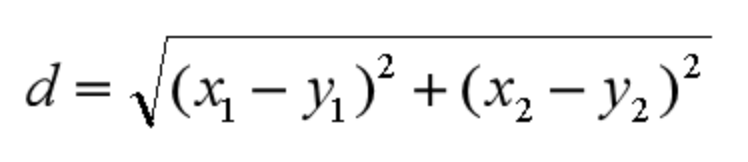
同理，我们也可以求得两点在 n 维空间中的距离：

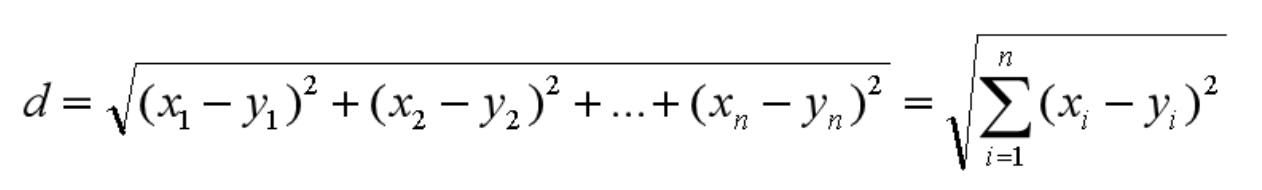
曼哈顿距离

在几何空间中用的比较多。曼哈顿距离等于两个点在坐标系上绝对轴距总和。用公式表示就是：

 

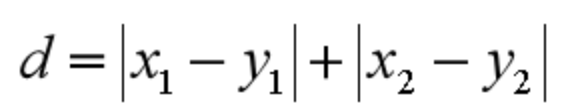
闵可夫斯基距离

不是一个距离，而是一组距离的定义。对于 n 维空间中的两个点 x(x1,x2,…,xn) 和 y(y1,y2,…,yn) ， x 和 y 两点之间的闵可夫斯基距离为：

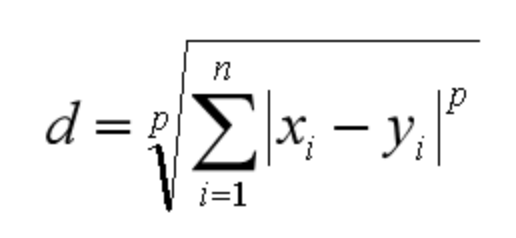
其中 p 代表空间的维数，当 p=1 时，就是曼哈顿距离；当 p=2 时，就是欧氏距离；当 p→∞时，就是切比雪夫距离。

那么切比雪夫距离 怎么计算呢？二个点之间的切比雪夫距离就是这两个点坐标数值差的绝对值的最大值，用数学表示就是：max(|x1-y1|,|x2-y2|)。

余弦距离 实际上计算的是两个向量的夹角，是在方向上计算两者之间的差异，对绝对数值不敏感。在兴趣相关性比较上，角度关系比距离的绝对值更重要，因此余弦距离可以用于衡量用户对内容兴趣的区分度。比如我们用搜索引擎搜索某个关键词，它还会给你推荐其他的相关搜索，这些推荐的关键词就是采用余弦距离计算得出的。

 

KD 树

其实从上文你也能看出来，KNN 的计算过程是大量计算样本点之间的距离。为了减少计算距离次数，提升 KNN 的搜索效率，人们提出了 KD 树（K-Dimensional 的缩写）。KD 树是对数据点在 K 维空间中划分的一种数据结构。在 KD 树的构造中，每个节点都是 k 维数值点的二叉树。既然是二叉树，就可以采用二叉树的增删改查操作，这样就大大提升了搜索效率。

在这里，我们不需要对 KD 树的数学原理了解太多，你只需要知道它是一个二叉树的数据结构，方便存储 K 维空间的数据就可以了。而且在 sklearn 中，我们直接可以调用 KD 树，很方便。

 

用 KNN 做回归

KNN 不仅可以做分类，还可以做回归。首先讲下什么是回归。在开头电影这个案例中，如果想要对未知电影进行类型划分，这是一个分类问题。首先看一下要分类的未知电影，离它最近的 K 部电影大多数属于哪个分类，这部电影就属于哪个分类。

如果是一部新电影，已知它是爱情片，想要知道它的打斗次数、接吻次数可能是多少，这就是一个回归问题。

那么 KNN 如何做回归呢？

对于一个新点，我们需要找出这个点的 K 个最近邻居，然后将这些邻居的属性的平均值赋给该点，就可以得到该点的属性。当然不同邻居的影响力权重可以设置成不同的。举个例子，比如一部电影 A，已知它是动作片，当 K=3 时，最近的 3 部电影是《战狼》，《红海行动》和《碟中谍 6》，那么它的打斗次数和接吻次数的预估值分别为 (100+95+105)/3=100 次、(5+3+31)/3=13 次。

 

三、 如何在 sklearn 中使用 KNN

接下来，我们先看下如何在 sklearn 中使用 KNN 算法，然后通过 sklearn 中自带的手写数字数据集来进行实战。

在 Python 的 sklearn 工具包中有 KNN 算法。KNN 既可以做分类器，也可以做回归。如果是做分类，你需要引用：

from sklearn.neighbors import KNeighborsClassifier

如果是做回归，你需要引用：

from sklearn.neighbors import KNeighborsRegressor

从名字上你也能看出来 Classifier 对应的是分类，Regressor 对应的是回归。一般来说如果一个算法有 Classifier 类，都能找到相应的 Regressor 类。比如在决策树分类中，你可以使用 DecisionTreeClassifier，也可以使用决策树来做回归 DecisionTreeRegressor。

好了，我们看下如何在 sklearn 中创建 KNN 分类器。

这里，我们使用构造函数 KNeighborsClassifier(n_neighbors=5, weights=‘uniform’, algorithm=‘auto’, leaf_size=30)，这里有几个比较主要的参数，我分别来讲解下：

1.n_neighbors：即 KNN 中的 K 值，代表的是邻居的数量。K 值如果比较小，会造成过拟合。如果 K 值比较大，无法将未知物体分类出来。一般我们使用默认值 5。

2.weights：是用来确定邻居的权重，有三种方式：

weights=uniform，代表所有邻居的权重相同；

weights=distance，代表权重是距离的倒数，即与距离成反比；

自定义函数，你可以自定义不同距离所对应的权重。大部分情况下不需要自己定义函数。

3.algorithm：用来规定计算邻居的方法，它有四种方式：

algorithm=auto，根据数据的情况自动选择适合的算法，默认情况选择 auto；

algorithm=kd_tree，也叫作 KD 树，是多维空间的数据结构，方便对关键数据进行检索，不过 KD 树适用于维度少的情况，一般维数不超过 20，如果维数大于 20 之后，效率反而会下降；

algorithm=ball_tree，也叫作球树，它和 KD 树一样都是多维空间的数据结果，不同于 KD 树，球树更适用于维度大的情况；

algorithm=brute，也叫作暴力搜索，它和 KD 树不同的地方是在于采用的是线性扫描，而不是通过构造树结构进行快速检索。当训练集大的时候，效率很低。

4.leaf_size：代表构造 KD 树或球树时的叶子数，默认是 30，调整 leaf_size 会影响到树的构造和搜索速度。

创建完 KNN 分类器之后，我们就可以输入训练集对它进行训练，这里我们使用 fit() 函数，传入训练集中的样本特征矩阵和分类标识，会自动得到训练好的 KNN 分类器。然后可以使用 predict() 函数来对结果进行预测，这里传入测试集的特征矩阵，可以得到测试集的预测分类结果。

 

四、 如何用 KNN 对手写数字进行识别分类

手写数字数据集是个非常有名的用于图像识别的数据集。数字识别的过程就是将这些图片与分类结果 0-9 一一对应起来。完整的手写数字数据集 MNIST 里面包括了 60000 个训练样本，以及 10000 个测试样本。如果你学习深度学习的话，MNIST 基本上是你接触的第一个数据集。

今天我们用 sklearn 自带的手写数字数据集做 KNN 分类，你可以把这个数据集理解成一个简版的 MNIST 数据集，它只包括了 1797 幅数字图像，每幅图像大小是 8*8 像素。

 

我们先来规划下整个 KNN 分类的流程：

数据加载：我们可以直接从 sklearn 中加载自带的手写数字数据集；

准备阶段：在这个阶段中，我们需要对数据集有个初步的了解，比如样本的个数、图像长什么样、识别结果是怎样的。你可以通过可视化的方式来查看图像的呈现。通过数据规范化可以让数据都在同一个数量级的维度。另外，因为训练集是图像，每幅图像是个 8*8 的矩阵，我们不需要对它进行特征选择，将全部的图像数据作为特征值矩阵即可；

分类阶段：通过训练可以得到分类器，然后用测试集进行准确率的计算。

 

好了，按照上面的步骤，我们一起来实现下这个项目。

首先是加载数据和对数据的探索：

# 加载数据
digits = load_digits()
data = digits.data
# 数据探索
print(data.shape)
# 查看第一幅图像
print(digits.images[0])
# 第一幅图像代表的数字含义
print(digits.target[0])
# 将第一幅图像显示出来
plt.gray()
plt.imshow(digits.images[0])
plt.show()

运行结果：

(1797, 64)
[[ 0.  0.  5. 13.  9.  1.  0.  0.]
[ 0.  0. 13. 15. 10. 15.  5.  0.]
[ 0.  3. 15.  2.  0. 11.  8.  0.]
[ 0.  4. 12.  0.  0.  8.  8.  0.]
[ 0.  5.  8.  0.  0.  9.  8.  0.]
[ 0.  4. 11.  0.  1. 12.  7.  0.]
[ 0.  2. 14.  5. 10. 12.  0.  0.]
[ 0.  0.  6. 13. 10.  0.  0.  0.]]
0

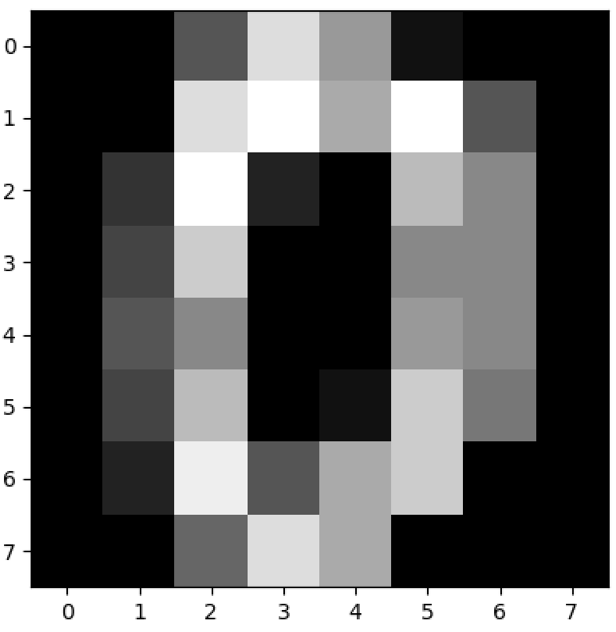
我们对原始数据集中的第一幅进行数据可视化，可以看到图像是个 8*8 的像素矩阵，上面这幅图像是一个“0”，从训练集的分类标注中我们也可以看到分类标注为“0”。

sklearn 自带的手写数字数据集一共包括了 1797 个样本，每幅图像都是 8*8 像素的矩阵。因为并没有专门的测试集，所以我们需要对数据集做划分，划分成训练集和测试集。因为 KNN 算法和距离定义相关，我们需要对数据进行规范化处理，采用 Z-Score 规范化，代码如下：

# 分割数据，将 25% 的数据作为测试集，其余作为训练集（你也可以指定其他比例的数据作为训练集）
train_x, test_x, train_y, test_y = train_test_split(data, digits.target, test_size=0.25, random_state=33)
# 采用 Z-Score 规范化
ss = preprocessing.StandardScaler()
train_ss_x = ss.fit_transform(train_x)
test_ss_x = ss.transform(test_x)
然后我们构造一个 KNN 分类器 knn，把训练集的数据传入构造好的 knn，并通过测试集进行结果预测，与测试集的结果进行对比，得到 KNN 分类器准确率，代码如下：
# 创建 KNN 分类器
knn = KNeighborsClassifier()
knn.fit(train_ss_x, train_y)
predict_y = knn.predict(test_ss_x)
print("KNN 准确率: %.4lf" % accuracy_score(predict_y, test_y))

运行结果：

KNN 准确率: 0.975

好了，这样我们就构造好了一个 KNN 分类器。之前我们还讲过 SVM、朴素贝叶斯和决策树分类。我们用手写数字数据集一起来训练下这些分类器，然后对比下哪个分类器的效果更好。代码如下：

# 创建 SVM 分类器
svm = SVC()
svm.fit(train_ss_x, train_y)
predict_y=svm.predict(test_ss_x)
print('SVM 准确率: %0.4lf' % accuracy_score(predict_y, test_y))
# 采用 Min-Max 规范化
mm = preprocessing.MinMaxScaler()
train_mm_x = mm.fit_transform(train_x)
test_mm_x = mm.transform(test_x)
# 创建 Naive Bayes 分类器
mnb = MultinomialNB()
mnb.fit(train_mm_x, train_y)
predict_y = mnb.predict(test_mm_x)
print(" 多项式朴素贝叶斯准确率: %.4lf" % accuracy_score(predict_y, test_y))
# 创建 CART 决策树分类器
dtc = DecisionTreeClassifier()
dtc.fit(train_mm_x, train_y)
predict_y = dtc.predict(test_mm_x)
print("CART 决策树准确率: %.4lf" % accuracy_score(predict_y, test_y))

运行结果如下：

SVM 准确率: 0.9867
多项式朴素贝叶斯准确率: 0.8844
CART 决策树准确率: 0.8556

这里需要注意的是，我们在做多项式朴素贝叶斯分类的时候，传入的数据不能有负数。因为 Z-Score 会将数值规范化为一个标准的正态分布，即均值为 0，方差为 1，数值会包含负数。因此我们需要采用 Min-Max 规范化，将数据规范化到 [0,1] 范围内。

好了，我们整理下这 4 个分类器的结果。

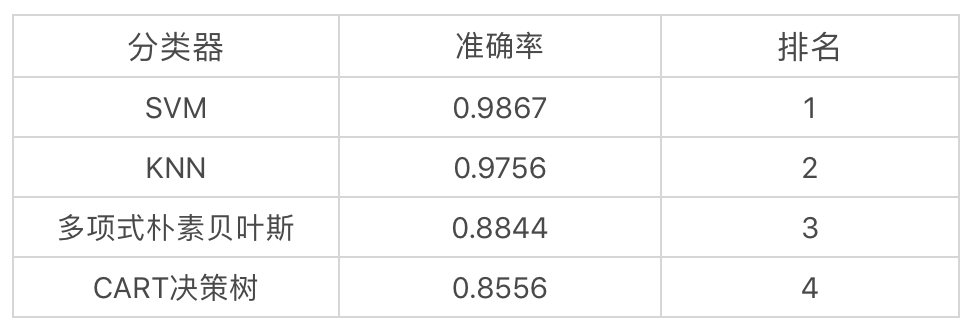
你能看出来 KNN 的准确率还是不错的，和 SVM 不相上下。

你可以自己跑一遍整个代码，在运行前还需要 import 相关的工具包（下面的这些工具包你都会用到，所以都需要引用）：

from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.metrics import accuracy_score
from sklearn.datasets import load_digits
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import MultinomialNB
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt

代码中，我使用了 train_test_split 做数据集的拆分，使用 matplotlib.pyplot 工具包显示图像，使用 accuracy_score 进行分类器准确率的计算，使用 preprocessing 中的 StandardScaler 和 MinMaxScaler 做数据的规范化。