机器学习经典算法之决策树
一、背景及问题
决策树算法是为了解决二分类问题出现的,是根据历史经验(或训练集)来做判断,生成决策结果(或树状图)的过程。
/*请尊重作者劳动成果,转载请标明原文链接:*/
/* https://www.cnblogs.com/jpcflyer/p/11037256.html * /
二、决策树原理
决策树算法分为两个阶段:构造和剪枝。
1.构造
什么是构造呢?构造就是生成一棵完整的决策树。简单来说, 构造的过程就是选择什么属性作为节点的过程 ,那么在构造过程中,会存在三种节点:
1)根节点:就是树的最顶端,最开始的那个节点。
2)内部节点:就是树中间的那些节点,比如说“温度”、“湿度”、“刮风”;
3)叶节点:就是树最底部的节点,也就是决策结果。
节点之间存在父子关系。比如根节点会有子节点,子节点会有子子节点,但是到了叶节点就停止了,叶节点不存在子节点。那么在构造过程中,你要解决三个重要的问题:
1)选择哪个属性作为根节点;
2)选择哪些属性作为子节点;
3)什么时候停止并得到目标状态,即叶节点。
2.剪枝
决策树构造出来之后是不是就万事大吉了呢?也不尽然,我们可能还需要对决策树进行剪枝。剪枝就是给决策树瘦身,这一步想实现的目标就是,不需要太多的判断,同样可以得到不错的结果。之所以这么做,是为了防止“过拟合”(Overfitting)现象的发生。
既然要对决策树进行剪枝,具体有哪些方法呢?一般来说,剪枝可以分为“预剪枝”(Pre-Pruning)和“后剪枝”(Post-Pruning)。
预剪枝是在决策树构造时就进行剪枝。方法是在构造的过程中对节点进行评估,如果对某个节点进行划分,在验证集中不能带来准确性的提升,那么对这个节点进行划分就没有意义,这时就会把当前节点作为叶节点,不对其进行划分。
后剪枝就是在生成决策树之后再进行剪枝,通常会从决策树的叶节点开始,逐层向上对每个节点进行评估。如果剪掉这个节点子树,与保留该节点子树在分类准确性上差别不大,或者剪掉该节点子树,能在验证集中带来准确性的提升,那么就可以把该节点子树进行剪枝。方法是:用这个节点子树的叶子节点来替代该节点,类标记为这个节点子树中最频繁的那个类。
三、决策树分类
现有打篮球的数据集,训练数据如下:
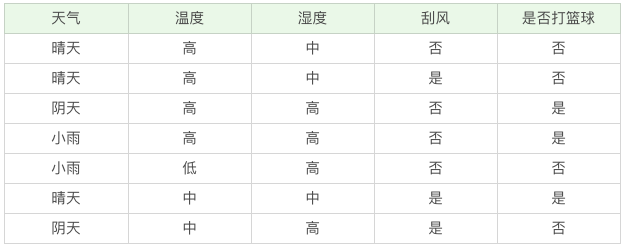
我们该如何构造一个判断是否去打篮球的决策树呢?再回顾一下决策树的构造原理,在决策过程中有三个重要的问题:将哪个属性作为根节点?选择哪些属性作为后继节点?什么时候停止并得到目标值?
显然将哪个属性(天气、温度、湿度、刮风)作为根节点是个关键问题,在这里我们先介绍两个指标:纯度和信息熵。
先来说一下纯度。你可以把决策树的构造过程理解成为寻找纯净划分的过程。数学上,我们可以用纯度来表示,纯度换一种方式来解释就是让目标变量的分歧最小。
我在这里举个例子,假设有 3 个集合:
集合 1:6 次都去打篮球;
集合 2:4 次去打篮球,2 次不去打篮球;
集合 3:3 次去打篮球,3 次不去打篮球。
按照纯度指标来说,集合 1> 集合 2> 集合 3。因为集合 1 的分歧最小,集合 3 的分歧最大。
然后我们再来介绍信息熵(entropy)的概念, 它表示了信息的不确定度。
在信息论中,随机离散事件出现的概率存在着不确定性。为了衡量这种信息的不确定性,信息学之父香农引入了信息熵的概念,并给出了计算信息熵的数学公式:
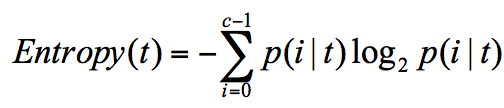
p(i|t) 代表了节点 t 为分类 i 的概率,其中 log2 为取以 2 为底的对数。这里我们不是来介绍公式的,而是说存在一种度量,它能帮我们反映出来这个信息的不确定度。当不确定性越大时,它所包含的信息量也就越大,信息熵也就越高。
我举个简单的例子,假设有 2 个集合
集合 1:5 次去打篮球,1 次不去打篮球;
集合 2:3 次去打篮球,3 次不去打篮球。
在集合 1 中,有 6 次决策,其中打篮球是 5 次,不打篮球是 1 次。那么假设:类别 1 为“打篮球”,即次数为 5;类别 2 为“不打篮球”,即次数为 1。那么节点划分为类别 1 的概率是 5/6,为类别 2 的概率是 1/6,带入上述信息熵公式可以计算得出:
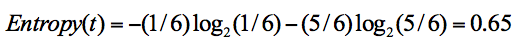
同样,集合 2 中,也是一共 6 次决策,其中类别 1 中“打篮球”的次数是 3,类别 2“不打篮球”的次数也是 3,那么信息熵为多少呢?我们可以计算得出:
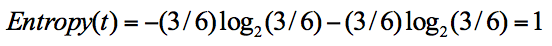
从上面的计算结果中可以看出,信息熵越大,纯度越低。当集合中的所有样本均匀混合时,信息熵最大,纯度最低。
我们在构造决策树的时候,会基于纯度来构建。而经典的 “不纯度”的指标有三种,分别是信息增益(ID3 算法)、信息增益率(C4.5 算法)以及基尼指数(Cart 算法)。
1.ID3
ID3 算法计算的是 信息增益 ,信息增益指的就是划分可以带来纯度的提高,信息熵的下降。它的计算公式,是父亲节点的信息熵减去所有子节点的信息熵。在计算的过程中,我们会计算每个子节点的归一化信息熵,即按照每个子节点在父节点中出现的概率,来计算这些子节点的信息熵。所以信息增益的公式可以表示为:
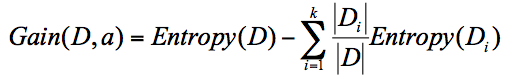
公式中 D 是父亲节点,Di 是子节点,Gain(D,a) 中的 a 作为 D 节点的属性选择。
假设天气 = 晴的时候,会有 5 次去打篮球,5 次不打篮球。其中 D1 刮风 = 是,有 2 次打篮球,1 次不打篮球。D2 刮风 = 否,有 3 次打篮球,4 次不打篮球。那么 a 代表节点的属性,即天气 = 晴。
针对这个例子,D 作为节点的信息增益为:

也就是 D 节点的信息熵 -2 个子节点的归一化信息熵。2 个子节点归一化信息熵 =3/10 的 D1 信息熵 +7/10 的 D2 信息熵。
我们基于 ID3 的算法规则,完整地计算下我们的训练集,训练集中一共有 7 条数据,3 个打篮球,4 个不打篮球,所以根节点的信息熵是:
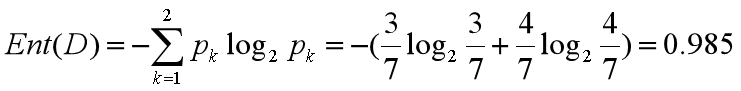
如果你将天气作为属性的划分,会有三个叶子节点 D1、D2 和 D3,分别对应的是晴天、阴天和小雨。我们用 + 代表去打篮球,- 代表不去打篮球。那么第一条记录,晴天不去打篮球,可以记为 1-,于是我们可以用下面的方式来记录 D1,D2,D3: D1(天气 = 晴天)={1-,2-,6+}
D2(天气 = 阴天)={3+,7-}
D3(天气 = 小雨)={4+,5-}
我们先分别计算三个叶子节点的信息熵:
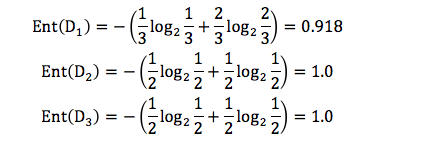
因为 D1 有 3 个记录,D2 有 2 个记录,D3 有 2 个记录,所以 D 中的记录一共是 3+2+2=7,即总数为 7。所以 D1 在 D(父节点)中的概率是 3/7,D2 在父节点的概率是 2/7,D3 在父节点的概率是 2/7。那么作为子节点的归一化信息熵 = 3/7*0.918+2/7*1.0+2/7*1.0=0.965。
因为我们用 ID3 中的信息增益来构造决策树,所以要计算每个节点的信息增益。
天气作为属性节点的信息增益为,Gain(D , 天气)=0.985-0.965=0.020。
同理我们可以计算出其他属性作为根节点的信息增益,它们分别为 :
Gain(D , 温度)=0.128
Gain(D , 湿度)=0.020
Gain(D , 刮风)=0.020
我们能看出来温度作为属性的信息增益最大。因为 ID3 就是要将信息增益最大的节点作为父节点,这样可以得到纯度高的决策树,所以我们将温度作为根节点。
然后我们要将第一个叶节点,也就是 D1={1-,2-,3+,4+}进一步进行分裂,往下划分,计算其不同属性(天气、湿度、刮风)作为节点的信息增益,可以得到:
Gain(D , 天气)=0
Gain(D , 湿度)=0
Gain(D , 刮风)=0.0615
我们能看到刮风为 D1 的节点都可以得到最大的信息增益,这里我们选取刮风作为节点。同理,我们可以按照上面的计算步骤得到完整的决策树。
于是我们通过 ID3 算法得到了一棵决策树。ID3 的算法规则相对简单,可解释性强。同样也存在缺陷,比如我们会发现 ID3 算法倾向于选择取值比较多的属性。这样,如果我们把“编号”作为一个属性(一般情况下不会这么做,这里只是举个例子),那么“编号”将会被选为最优属性 。但实际上“编号”是无关属性的,它对“打篮球”的分类并没有太大作用。
所以 ID3 有一个缺陷就是,有些属性可能对分类任务没有太大作用,但是他们仍然可能会被选为最优属性。这种缺陷不是每次都会发生,只是存在一定的概率。在大部分情况下,ID3 都能生成不错的决策树分类。针对可能发生的缺陷,后人提出了新的算法进行改进。
2.C4.5
C4.5是在ID3的基础上做了改进。 那么 C4.5 都在哪些方面改进了 ID3 呢?
1)采用信息增益率
因为 ID3 在计算的时候,倾向于选择取值多的属性。为了避免这个问题,C4.5 采用信息增益率的方式来选择属性。信息增益率 = 信息增益 / 属性熵,具体的计算公式这里省略。
当属性有很多值的时候,相当于被划分成了许多份,虽然信息增益变大了,但是对于 C4.5 来说,属性熵也会变大,所以整体的信息增益率并不大。
2)采用悲观剪枝
ID3 构造决策树的时候,容易产生过拟合的情况。在 C4.5 中,会在决策树构造之后采用悲观剪枝(PEP),这样可以提升决策树的泛化能力。
悲观剪枝是后剪枝技术中的一种,通过递归估算每个内部节点的分类错误率,比较剪枝前后这个节点的分类错误率来决定是否对其进行剪枝。这种剪枝方法不再需要一个单独的测试数据集。
3)离散化处理连续属性
C4.5 可以处理连续属性的情况,对连续的属性进行离散化的处理。比如打篮球存在的“湿度”属性,不按照“高、中”划分,而是按照湿度值进行计算,那么湿度取什么值都有可能。该怎么选择这个阈值呢, C4.5 选择具有最高信息增益的划分所对应的阈值。
4)处理缺失值
针对数据集不完整的情况,C4.5 也可以进行处理。
假如我们得到的是如下的数据,你会发现这个数据中存在两点问题。第一个问题是,数据集中存在数值缺失的情况,如何进行属性选择?第二个问题是,假设已经做了属性划分,但是样本在这个属性上有缺失值,该如何对样本进行划分?
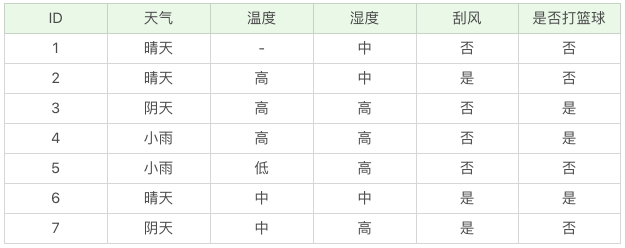
我们不考虑缺失的数值,可以得到温度 D={2-,3+,4+,5-,6+,7-}。温度 = 高:D1={2-,3+,4+} ;温度 = 中:D2={6+,7-};温度 = 低:D3={5-} 。这里 + 号代表打篮球,- 号代表不打篮球。比如 ID=2 时,决策是不打篮球,我们可以记录为 2-。
所以三个叶节点的信息熵可以结算为:
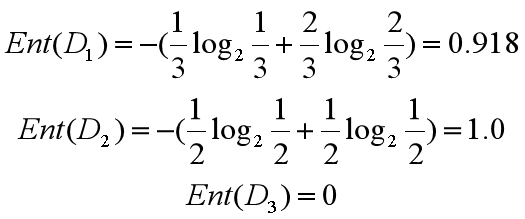
这三个节点的归一化信息熵为 3/6*0.918+2/6*1.0+1/6*0=0.792。
针对将属性选择为温度的信息增益率为:
Gain(D′, 温度)=Ent(D′)-0.792=1.0-0.792=0.208
D′的样本个数为 6,而 D 的样本个数为 7,所以所占权重比例为 6/7,所以 Gain(D′,温度) 所占权重比例为 6/7,所以:
Gain(D, 温度)=6/7*0.208=0.178
这样即使在温度属性的数值有缺失的情况下,我们依然可以计算信息增益,并对属性进行选择。
3.CART
CART 算法,英文全称叫做 Classification And Regression Tree,中文叫做分类回归树。ID3 和 C4.5 算法可以生成二叉树或多叉树,而 CART 只支持二叉树。同时 CART 决策树比较特殊,既可以作分类树,又可以作回归树。
那么你首先需要了解的是,什么是分类树,什么是回归树呢?
我用下面的训练数据举个例子,你能看到不同职业的人,他们的年龄不同,学习时间也不同。如果我构造了一棵决策树,想要基于数据判断这个人的职业身份,这个就属于分类树,因为是从几个分类中来做选择。如果是给定了数据,想要预测这个人的年龄,那就属于回归树。
分类树可以处理离散数据,也就是数据种类有限的数据,它输出的是样本的类别,而回归树可以对连续型的数值进行预测,也就是数据在某个区间内都有取值的可能,它输出的是一个数值。
1)CART 分类树的工作流程
CART 分类树与 C4.5 算法类似,只是属性选择的指标采用的是基尼系数。
你可能在经济学中听过说基尼系数,它是用来衡量一个国家收入差距的常用指标。当基尼系数大于 0.4 的时候,说明财富差异悬殊。基尼系数在 0.2-0.4 之间说明分配合理,财富差距不大。
基尼系数本身反应了样本的不确定度。当基尼系数越小的时候,说明样本之间的差异性小,不确定程度低。分类的过程本身是一个不确定度降低的过程,即纯度的提升过程。所以 CART 算法在构造分类树的时候,会选择基尼系数最小的属性作为属性的划分。
我们接下来详解了解一下基尼系数。基尼系数不好懂,你最好跟着例子一起手动计算下。
假设 t 为节点,那么该节点的 GINI 系数的计算公式为:
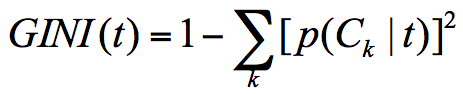
这里 p(Ck|t) 表示节点 t 属于类别 Ck 的概率,节点 t 的基尼系数为 1 减去各类别 Ck 概率平方和。
通过下面这个例子,我们计算一下两个集合的基尼系数分别为多少:
集合 1:6 个都去打篮球;
集合 2:3 个去打篮球,3 个不去打篮球。
针对集合 1,所有人都去打篮球,所以 p(Ck|t)=1,因此 GINI(t)=1-1=0。
针对集合 2,有一半人去打篮球,而另一半不去打篮球,所以,p(C1|t)=0.5,p(C2|t)=0.5,GINI(t)=1-(0.5*0.5+0.5*0.5)=0.5。
通过两个基尼系数你可以看出,集合 1 的基尼系数最小,也证明样本最稳定,而集合 2 的样本不稳定性更大。
在 CART 算法中,基于基尼系数对特征属性进行二元分裂,假设属性 A 将节点 D 划分成了 D1 和 D2,如下图所示:
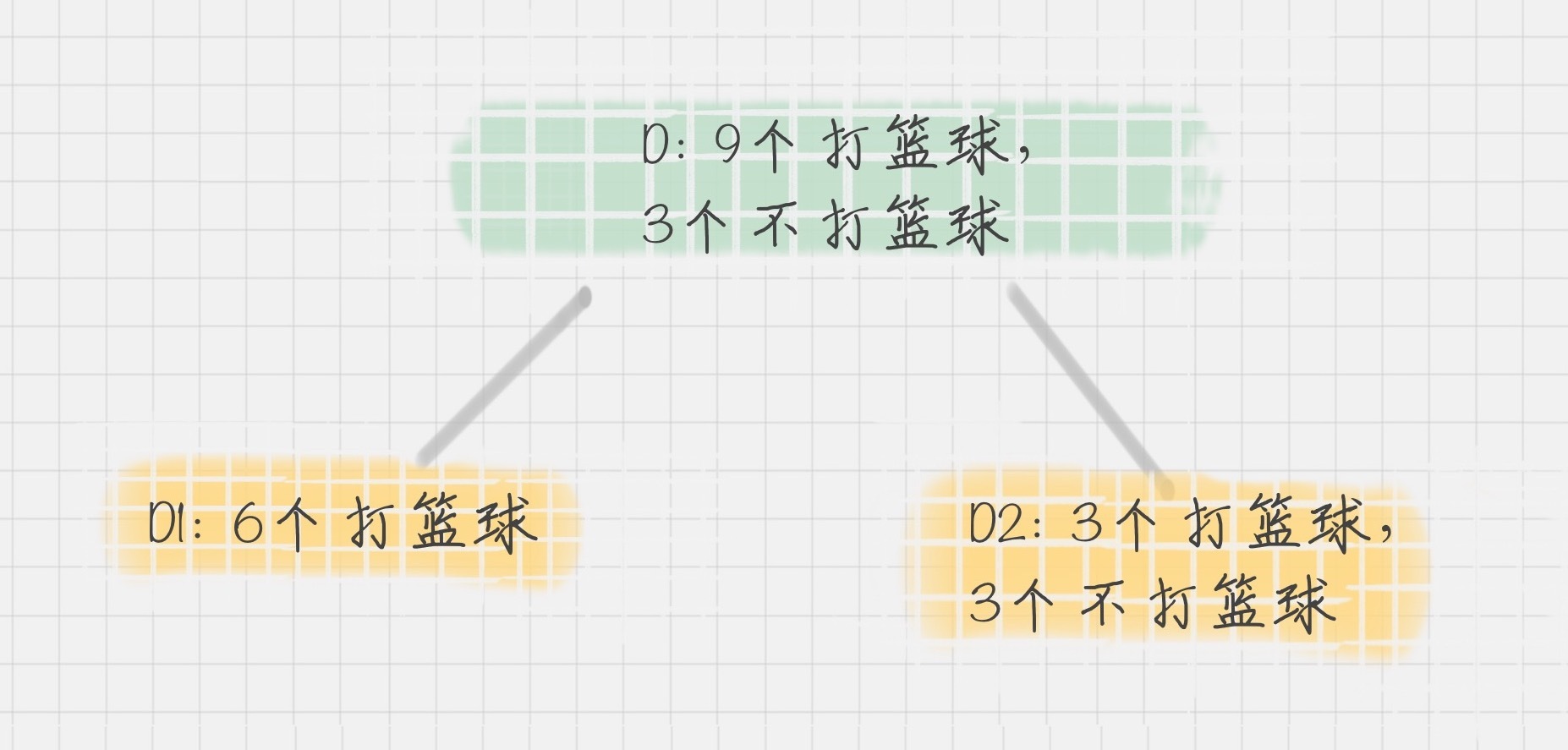
节点 D 的基尼系数等于子节点 D1 和 D2 的归一化基尼系数之和,用公式表示为:
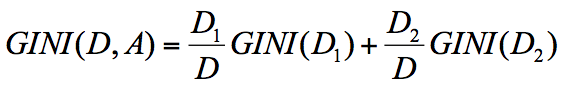
归一化基尼系数代表的是每个子节点的基尼系数乘以该节点占整体父亲节点 D 中的比例。
上面我们已经计算了集合 D1 和集合 D2 的 GINI 系数,得到:

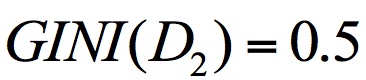
所以节点 D 的基尼系数为:

节点 D 被属性 A 划分后的基尼系数越大,样本集合的不确定性越大,也就是不纯度越高。
2) 如何使用 CART 算法来创建分类树
通过上面的讲解你可以知道,CART 分类树实际上是基于基尼系数来做属性划分的。在 Python 的 sklearn 中,如果我们想要创建 CART 分类树,可以直接使用 DecisionTreeClassifier 这个类。创建这个类的时候,默认情况下 criterion 这个参数等于 gini,也就是按照基尼系数来选择属性划分,即默认采用的是 CART 分类树。
下面,我们来用 CART 分类树,给 iris 数据集构造一棵分类决策树。iris 这个数据集,我在 Python 可视化中讲到过,实际上在 sklearn 中也自带了这个数据集。基于 iris 数据集,构造 CART 分类树的代码如下:
1 # encoding=utf-8
2 from sklearn.model_selection import train_test_split
3 from sklearn.metrics import accuracy_score
4 from sklearn.tree import DecisionTreeClassifier
5 from sklearn.datasets import load_iris
6 # 准备数据集
7 iris=load_iris()
8 # 获取特征集和分类标识
9 features = iris.data
10 labels = iris.target
11 # 随机抽取 33% 的数据作为测试集,其余为训练集
12 train_features, test_features, train_labels, test_labels = train_test_split(features, labels, test_size=0.33, random_state=0)
13 # 创建 CART 分类树
14 clf = DecisionTreeClassifier(criterion='gini')
15 # 拟合构造 CART 分类树
16 clf = clf.fit(train_features, train_labels)
17 # 用 CART 分类树做预测
18 test_predict = clf.predict(test_features)
19 # 预测结果与测试集结果作比对
20 score = accuracy_score(test_labels, test_predict)
21 print("CART 分类树准确率 %.4lf" % score)
运行结果:
1 CART 分类树准确率 0.9600
3) CART 回归树的工作流程
CART 回归树划分数据集的过程和分类树的过程是一样的,只是回归树得到的预测结果是连续值,而且评判“不纯度”的指标不同。在 CART 分类树中采用的是基尼系数作为标准,那么在 CART 回归树中,如何评价“不纯度”呢?实际上我们要根据样本的混乱程度,也就是样本的离散程度来评价“不纯度”。
样本的离散程度具体的计算方式是,先计算所有样本的均值,然后计算每个样本值到均值的差值。我们假设 x 为样本的个体,均值为 u。为了统计样本的离散程度,我们可以取差值的绝对值,或者方差。
其中差值的绝对值为样本值减去样本均值的绝对值:
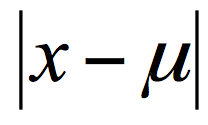
方差为每个样本值减去样本均值的平方和除以样本个数:
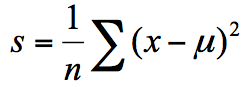
所以这两种节点划分的标准,分别对应着两种目标函数最优化的标准,即用最小绝对偏差(LAD),或者使用最小二乘偏差(LSD)。这两种方式都可以让我们找到节点划分的方法,通常使用最小二乘偏差的情况更常见一些。
我们可以通过一个例子来看下如何创建一棵 CART 回归树来做预测。
4)如何使用 CART 回归树做预测
这里我们使用到 sklearn 自带的波士顿房价数据集,该数据集给出了影响房价的一些指标,比如犯罪率,房产税等,最后给出了房价。
根据这些指标,我们使用 CART 回归树对波士顿房价进行预测,代码如下:
1 # encoding=utf-8
2 from sklearn.metrics import mean_squared_error
3 from sklearn.model_selection import train_test_split
4 from sklearn.datasets import load_boston
5 from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
6 from sklearn.tree import DecisionTreeRegressor
7 # 准备数据集
8 boston=load_boston()
9 # 探索数据
10 print(boston.feature_names)
11 # 获取特征集和房价
12 features = boston.data
13 prices = boston.target
14 # 随机抽取 33% 的数据作为测试集,其余为训练集
15 train_features, test_features, train_price, test_price = train_test_split(features, prices, test_size=0.33)
16 # 创建 CART 回归树
17 dtr=DecisionTreeRegressor()
18 # 拟合构造 CART 回归树
19 dtr.fit(train_features, train_price)
20 # 预测测试集中的房价
21 predict_price = dtr.predict(test_features)
22 # 测试集的结果评价
23 print('回归树二乘偏差均值:', mean_squared_error(test_price, predict_price))
24 print('回归树绝对值偏差均值:', mean_absolute_error(test_price, predict_price))
运行结果(每次运行结果可能会有不同):
1 ['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO' 'B' 'LSTAT']
2 回归树二乘偏差均值: 23.80784431137724
3 回归树绝对值偏差均值: 3.040119760479042
5) CART 决策树的剪枝
CART 决策树的剪枝主要采用的是 CCP 方法,它是一种后剪枝的方法,英文全称叫做 cost-complexity prune,中文叫做代价复杂度。这种剪枝方式用到一个指标叫做节点的表面误差率增益值,以此作为剪枝前后误差的定义。用公式表示则是:
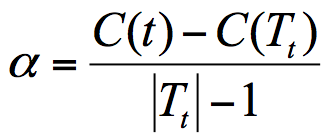
其中 Tt 代表以 t 为根节点的子树,C(Tt) 表示节点 t 的子树没被裁剪时子树 Tt 的误差,C(t) 表示节点 t 的子树被剪枝后节点 t 的误差,|Tt|代子树 Tt 的叶子数,剪枝后,T 的叶子数减少了|Tt|-1。
所以节点的表面误差率增益值等于节点 t 的子树被剪枝后的误差变化除以剪掉的叶子数量。
因为我们希望剪枝前后误差最小,所以我们要寻找的就是最小α值对应的节点,把它剪掉。这时候生成了第一个子树。重复上面的过程,继续剪枝,直到最后只剩下根节点,即为最后一个子树。
得到了剪枝后的子树集合后,我们需要用验证集对所有子树的误差计算一遍。可以通过计算每个子树的基尼指数或者平方误差,取误差最小的那个树,得到我们想要的结果。
四、总结
最后我们来整理下三种决策树之间在属性选择标准上的差异:
ID3 算法,基于信息增益做判断;
C4.5 算法,基于信息增益率做判断;
CART 算法,分类树是基于基尼系数做判断。回归树是基于偏差做判断。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号