7、Logistic回归
logistic回归是使用最多的分类算法
二分类
预测值:yε{0, 1}, 0代表负类(No, 假设不成立);1代表正类(Yes,假设成立)
应用:邮件分类(垃圾邮件 or 非垃圾邮件)
假设函数
logistic函数又称Sigmoid函数,是一个在生物学中常见的S型函数,也称为S型生长曲线。由于其单增以及反函数单增等性质,常被用作神经网络等阀值函数,将变量映射到0-1之间,所以logistic函数到预测值:0≤y≤1
logistic方程式:g(z) = 1/(1 + e-z),0≤g(z)≤1
线性回归假设函数:h(x) = θTx
所以,logistic假设函数:h(x) = g(θTx) = 1/(1 + e-θTx),0≤h(x)≤1
logistic模型解释
因为预测值y只能取值0或者1,根据概率在给定参数θ下概率P(y=1)和P(y=0)的和为1,即:P(y=0;θ) + P(y=1;θ) = 1
决策界限
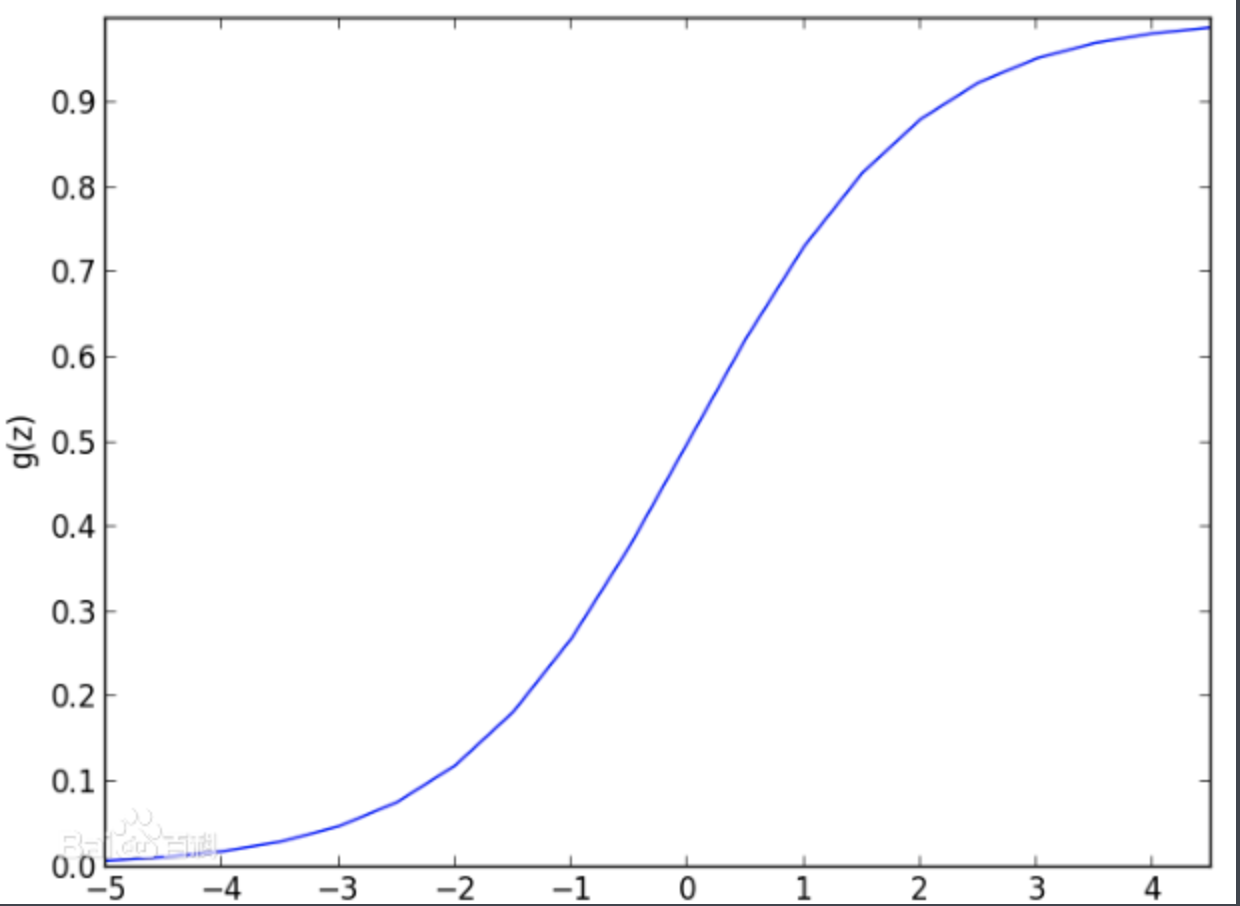
根据logistic图形
- h(z)≥0.5,y=1; 由h(z)=g(θTx)≥0.5,推出z≥0, 即θTx≥0
- h(z)<0.5,y=0;由h(z)=g(θTx)<0.5,推出z<0, 即θTx<0
所以z=0是假设函数的决策界限,决策界限是假设函数的一个属性,它把假设函数图形分成两半:y=0和y=1
损失函数
训练集:{(x1,y1),(x2,y2),(x3,y3),...,(xm,ym)} ,m个样本
X = [x0 x1 ... xm]T, x0=1, yε{0, 1}
h(x) = 1/(1 + e-θTx)
线性回归损失函数:J(θ)=Σ(h(xi)-yi)2/m, iε{1, m}
令Cost(h(xi),yi)=(h(xi)-yi)2
所以,J(θ)=Σ(h(xi)-yi)2/m=ΣCost(h(xi),yi)/m, iε{1, m}
损失函数:
- Cost(h(x), y)=-log(h(x)), y=1
- Cost(h(x), y)= -log(1-h(x)), y=0
结合图形:
1、当y=1:
- h(x)=1时,Cost=0,损失函数值最小
- h(x)=0时,Cost=∞,损失函数值最大
2、当y=0:
- h(x)=0时,Cost=0,损失函数值最小
- h(x)=1时,Cost=∞,损失函数值最大
简化损失函数和梯度下降
J(θ)=Σ(h(xi)-yi)2/m=ΣCost(h(xi),yi)/m, iε{1, m}
Cost(h(x), y)=-log(h(x)), y=1
Cost(h(x), y)= -log(1-h(x)), y=0
简化损失函数:
Cost(h(x), y)=-log(h(x))-(1-y)log(1-h(x))
所以梯度下降:J(θ)=Σ(h(xi)-yi)2/m=-Σyilog(h(xi))+(1-yi)log(1-h(xi))/m, iε{1, m}
简化损失函数和梯度下降
minJ(θ): repeat{ θj := θj-α(∂/∂θj)J(θ)}
梯度下降和缩放同样适用于logistic回归
高级优化方法
- cojugate gradient
- BFGS
- L-BFGS
以上三种算法的优点:不需要选择学习率,比梯度下降收敛速度快
缺点:比梯度下降算法复杂
多分类问题
简化为二分类问题来处理,比如三分类简化为三个二分类来处理



