各种特殊矩阵总结

一般在实际运用中，矩阵本身或者都需要化成特殊的形式。列出一些常用的矩阵形式。

reference: en.wikipedia.org

1. Toeplitz matrix，形如

\begin{bmatrix} a & b & c & d & e \\ f & a & b & c & d \\ g & f & a & b & c \\ h & g & f & a & b \\ i & h & g & f & a \end{bmatrix}.

2. Hankel matix，形如

\begin{bmatrix} a & b & c & d & e \\ b & c & d & e & f \\ c & d & e & f & g \\ d & e & f & g & h \\ e & f & g & h & i \\ \end{bmatrix}.

刚好和就是toeplitz的transpose

3. Degree matrix，这个和拓扑学有关了，此矩阵只有main diagonal上有非零值，代表的是对应edge(node)所连接的vetices的数量（如果自循环则算两个）

G=(V,E)， \|V\|=n

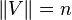
对该图形而言，这个E对应的位置就应该填上n。每个E都算完后，其余位置均为0。

4. Adjacency matrix，也和拓扑学有关，为仅有1或者0的矩阵。

如果两个edge之间有vertex相连，则对应位置填1。因为这个性质，此矩阵为symmetric的，main diagonal上的1表示自循环。

5. Laplacian matix。由上面两位计算得到

L=D-A

6. Circulant matrix, T的变种，如下

C= \begin{bmatrix} c_0 & c_{n-1} & \dots & c_{2} & c_{1} \\ c_{1} & c_0 & c_{n-1} & & c_{2} \\ \vdots & c_{1}& c_0 & \ddots & \vdots \\ c_{n-2} & & \ddots & \ddots & c_{n-1} \\ c_{n-1} & c_{n-2} & \dots & c_{1} & c_0 \\ \end{bmatrix}.

7. Symplectic matrix

指满足这个条件的M（2n*2n）矩阵：M^T \Omega M = \Omega\,.

其中，另一个矩阵必须是nonsingular, skew-symmetric matrix.，例如选　　\Omega = \begin{bmatrix} 0 & I_n \\ -I_n & 0 \\ \end{bmatrix}

是一个block matrix，I是单位矩阵(identity matix)。


8. Vandermonde matrix，形如

V=\begin{bmatrix} 1 & \alpha_1 & \alpha_1^2 & \dots & \alpha_1^{n-1}\\ 1 & \alpha_2 & \alpha_2^2 & \dots & \alpha_2^{n-1}\\ 1 & \alpha_3 & \alpha_3^2 & \dots & \alpha_3^{n-1}\\ \vdots & \vdots & \vdots & \ddots &\vdots \\ 1 & \alpha_m & \alpha_m^2 & \dots & \alpha_m^{n-1} \end{bmatrix}

 

9. Hessenberg matrix

Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular. To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal

例如：upper Hessenberg matrix

\begin{bmatrix} 1 & 4 & 2 & 3 \\ 3 & 4 & 1 & 7 \\ 0 & 2 & 3 & 4 \\ 0 & 0 & 1 & 3 \\ \end{bmatrix}

10. Hessian matrix

对于实数函数 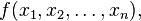f(x_1, x_2, \dots, x_n),\,\! 求二阶偏导（second-order partial derivatives），如下

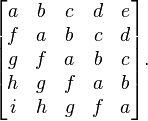
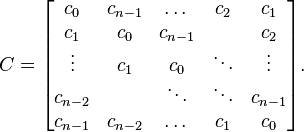
H(f) = \begin{bmatrix} \dfrac{\partial^2 f}{\partial x_1^2} & \dfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \dfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[2.2ex] \dfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \dfrac{\partial^2 f}{\partial x_2^2} & \cdots & \dfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[2.2ex] \vdots & \vdots & \ddots & \vdots \\[2.2ex] \dfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \dfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \dfrac{\partial^2 f}{\partial x_n^2} \end{bmatrix}.

 

 

posted @ 2012-12-02 19:39  joywelt  阅读(8272)  评论(1)  编辑  收藏  举报