穿过地心要多久？

原文链接：Journey through the center of the Earth

里约奥运会闭幕式上，日本首相化身超级马里奥穿越地心

跳入贯穿地球的洞

假设你在地球上钻个洞，然后跳进去，多长时间你会从另一端跑出来？

在地球表面上的重力加速度为

\begin{equation*} g=\frac{GM_地}{R^2}=9.8\mathrm{m/s^2} \end{equation*}

其中\(M_地\)为地球质量，\(R\)为地球半径。

但是随着你在洞里下落，越来越接近地心，你重力加速度也越来越小。当你正好到达地心的时候，重力加速度为0。假设地球完美球体，质量均匀分布，忽略空气阻力，忽略地球内部的高温，则当你距离球心\(r\)处时，等效重力加速度

\begin{equation*} g_{等效}=\frac{GM(r)}{r^2}=\frac{G}{r^2}\left (\rho\frac{4\pi}{3}r^3\right ) \end{equation*}

而地球密度为

\begin{equation*} \rho=\frac{M_地}{\frac{4\pi}{3}R^3} \end{equation*}

于是

\begin{equation*} g_{等效}=\frac{GM(r)}{r^2}=\frac{G}{r^2}\left (\rho\frac{4\pi}{3}r^3\right )=\frac{GM_地}{R^2}\frac{r}{R}=g\frac{r}{R} \end{equation*}

地球内部某一点处的你的重力与该点到地心的半径成正比。

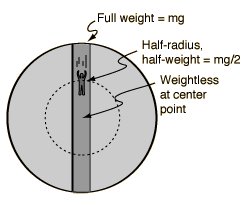
地表处重力为\(mg\)，下落到地球半径一半处，重力为\(mg/2\)，下落到地心处，重力为0

取\(r\)的正方向为从地心指向地球外部，则当你下落到距离地心\(r\)处时受力为

\begin{equation*} F=-mg\frac{r}{R}=-kr \end{equation*}

与拴在弹簧上的物体所受的力是一样的。于是可知，跳入地球的你将做简谐振动，振动的周期为

\begin{equation*} \begin{split} T=&2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{m}{mg/R}}=2\pi\sqrt{\frac{R}{g}} \\ =&2\pi\sqrt{\frac{6.378\times 10^6}{9.8}}\mathrm s=5068\mathrm s=84.5 \mathrm {min} \end{split} \end{equation*}

即大约42分钟后你跑到地球另一端，但是注意，一定要扒住洞口，否则会返回来。没扒住，也不用着急，你会在洞里往复运动，每84.5分钟就有一次扒住洞口的机会。

不过，等你到达洞的另一端，可能没有机会扒洞口，因为你在洞里早挂了。在洞口你相对地心有个水平方向的速度，这个速度高达\(465\mathrm {m/s}=1674\mathrm {km/h}\)，比飞机速度还要大，以这个速度与洞壁碰撞，能不挂吗？所以，还是离洞远一点吧。