杨氏双缝干涉
考虑频率相同,振动方向相同,具有恒定初始相位的两列波的叠加。设这两列波从空间两定点\(S_1\)和\(S_2\)发出,波源的振动可分别表示为
\begin{equation*} \psi_{01}=A_1\cos\left (\omega t+\varphi_{01} \right) \end{equation*}
\begin{equation}
\psi_{02}=A_2\cos\left (\omega t+\varphi_{02} \right)
\end{equation}
其中\(\varphi_{01}\)和\(\varphi_{02}\)分别是两波源振动的初相位。两列波同时到达空间一点\(P\)处,\(P\)点到两波源的距离分别是\(r_1\)和\(r_2\),波速分别为\(v_1\)和\(v_2\),如下图所示,

图1
则\(P\)点处的振动为
\begin{equation*} \psi_1=A_1\cos\left [\omega\left (t-\frac{r_1}{v_1}\right)+\varphi_{01} \right ]=A_1\cos\left (\omega t+\varphi_{1} \right) \end{equation*}
\begin{equation}
\psi_2=A_2\cos\left [\omega\left (t-\frac{r_2}{v_2}\right)+\varphi_{02} \right ]=A_2\cos\left (\omega t+\varphi_{2} \right)
\end{equation}
合振动强度
\begin{equation*} I=A^2=I_1+I_2+2\sqrt{I_1I_2}\cos\Delta \varphi \end{equation*}
其中相位差为
\begin{equation*} \Delta \varphi = \omega\left (\frac{r_2}{v_2}-\frac{r_1}{v_1}\right )-(\varphi_{02}-\varphi_{01}) \end{equation*}
如果两振动相位相同,
\begin{equation*} \Delta \varphi = \pm 2k\pi, k=0,1,2,\dots \end{equation*}
合振动强度达到最大,称为干涉相长。
如果两振动相位相反,
\begin{equation*} \Delta \varphi = \pm (2k+1)\pi, k=0,1,2,\dots \end{equation*}
合振动强度达到最小,称为干涉相消。
对于光波,相位差
\begin{equation*} \begin{split} \Delta \varphi &= \omega\left (\frac{r_2}{v_2}-\frac{r_1}{v_1}\right )-(\varphi_{02}-\varphi_{01})\\ &=\frac{2\pi c}{\lambda}\left (\frac{r_2}{v_2}-\frac{r_1}{v_1}\right )-(\varphi_{02}-\varphi_{01})\\ &=\frac{2\pi }{\lambda}(n_2r_2-n_1r_1)-(\varphi_{02}-\varphi_{01}) \end{split} \end{equation*}
其中\(\lambda\)为波在真空中的波长,\(n_1=c/v_1\)和\(n_2=c/v_2\)分别为两波在传播路径上所经介质的折射率。
可见,相位差取决于两个因素,一是波源振动的相位差,二是折射率与路程之积的差。折射率与路程的乘积叫做光程,
\begin{equation*} \Delta = nr \end{equation*}
\(\delta =n_2r_2-n_1r_1\)叫做光程差。
现在我们讨论最简单的情况,\(\varphi_{02}=\varphi_{01}\),\(n=1\),杨氏双缝实验就属于这一情况。杨氏双缝实验如图2所示。其中\(S\)是点光源,\(G\)是遮光板,其上开有两条平行的狭缝\(S_1\)和\(S_2\),间距为\(d\)。\(H\)为观察屏,与\(G\)距离为\(D\),在实验条件下\(D\gg d\)。\(S_1\)和\(S_2\)是同一波面上的两点,可看作新的波源,发出的次波在遮光板后面的空间叠加,这两束波的初相位相同。

图2 杨氏双缝干涉实验
相位差唯一取决于几何路程差
\begin{equation*} \Delta \varphi = \frac{2\pi }{\lambda}(r_2-r_1) \end{equation*}
于是,出现相长干涉的条件是
\begin{equation*} r_2-r_1 = \pm k\lambda = \pm (2k)\frac{\lambda}{2}, k=0,1,2,\dots \end{equation*}
即光程差是半波长的偶数倍。
出现相消干涉的条件是
\begin{equation*} r_2-r_1 = \pm (2k+1)\frac{\lambda}{2}, k=0,1,2,\dots \end{equation*}
即光程差是半波长的奇数倍。
如图2所示,\(r_1,r_2\gg d\),\(S_1P\)与\(S_2P\)可近似看做平行,于是
\begin{equation*} r_2-r_1 \approx d\sin \theta \end{equation*}
其中\(\theta\)为\(P\)点的角位置。
上式可以由数学得到。
\begin{equation*} \begin{split} r_2 &= \sqrt{r^2+\frac{d^2}{4}-rd\cos\left (\frac{\pi}{2}+\theta \right )\sin \theta}\\ \\ &= \sqrt{r^2+\frac{d^2}{4}+rd\sin \theta}= r\sqrt{1+\frac{d^2}{4r^2}+\frac{d}{r}\sin \theta}\\ &\approx r\sqrt{1+\frac{d}{r}\sin \theta} \quad (约去二阶小量) \\ &\approx r\left (1+\frac{d}{r}\sin \theta \right)\quad (泰勒展开保留至一阶小量) \end{split} \end{equation*}
同理,
\begin{equation*} r_1 \approx r\left (1-\frac{d}{r}\sin \theta \right) \end{equation*}
于是有\(r_2-r_1 \approx d\sin \theta\)。
\(P\)点坐标与角位置关系为
\begin{equation*} x= D\tan\theta\approx D\sin \theta \end{equation*}
于是可得相长干涉(亮条纹)的位置为
\begin{equation*} r_2-r_1 = d\sin \theta=\frac{dx}{D}=\pm k\lambda = \pm (2k)\frac{\lambda}{2}, k=0,1,2,\dots \end{equation*}
出现相消干涉(暗条纹)的条件是
\begin{equation*} r_2-r_1 =d\sin \theta=\frac{dx}{D}= \pm (2k+1)\frac{\lambda}{2}, k=0,1,2,\dots \end{equation*}
即出现亮条纹的位置为
\begin{equation*} x =\pm k \frac{D}{d}\lambda, k=0,1,2,\dots \end{equation*}
即出现暗条纹的位置为
\begin{equation*} x =\pm (2k-1) \frac{D}{d}\lambda, k=0,1,2,\dots \end{equation*}
其中,\(k\)称为条纹的级次。
相邻明(或暗)条纹的间距为
\begin{equation*} \Delta x =\frac{D}{d}\lambda \end{equation*}
条纹是等间距排列的。条纹间距与双缝到观察屏的距离成正比,与双缝间距成反比。

条纹间距与双缝间距成反比。
条纹间距与波长成正比。

条纹间距与波长成正比
如果用白光做光源,除中央亮条纹外,起于各级条纹都带有各种颜色。对于级数较大的条纹,不同级次的条纹因互相重叠而使条纹模糊,因此用白光做干涉实验可以辨认的条纹数目很少,实验一般采用单色光。
现在讨论,观察屏上光强的分布。设两列波的光强相等,均为\(I_0\),则叠加之后的光强为
\begin{equation*} \begin{split} I&=A^2=I_0+I_0+2I_0\cos\Delta \varphi = 2I_0(1+\cos\Delta \varphi)=4I_0\cos^2\frac{\Delta\varphi}{2}\\ &=4I_0\cos^2\frac{\pi d\sin\theta}{\lambda}=4I_0\cos^2\frac{\pi dx}{D\lambda} \end{split} \end{equation*}


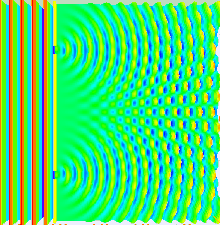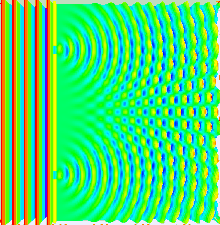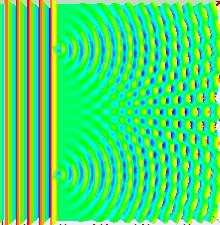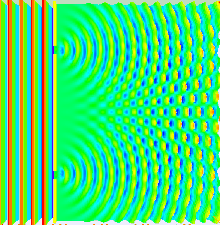 让一束光入射到两个很靠近的狭缝上,从狭缝出射的两束光具有确定的相位关系,可以发生干涉。
让一束光入射到两个很靠近的狭缝上,从狭缝出射的两束光具有确定的相位关系,可以发生干涉。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号