我的电磁学讲义9：磁简史 磁的基本现象 安培定律

磁简史

中国古籍对磁现象有所记载，如《管子·地数篇》（上有慈石者，其下有铜金）、《山海经·北山经》（又北三百二十里，曰灌题之山，其上多樗柘，其下多流沙，多砥。有兽焉，其状如牛而白尾，其音如詨，名曰那父。有鸟焉，其状如雌雉而人面，见人则跃，名曰竦斯，其鸣自呼也。匠韩之水出焉，而西流注于泑泽，其中多磁石。）、《鬼谷子·反应》（其察言也不失，若磁石之取铁）、《吕氏春秋·精通》（慈石召铁，或引之也。）

中国古籍还记载有指南的仪器。王充《论衡·是应篇》：“司南之杓，投之于地，其柢指南。”司南勺是今人无法复原的仪器。（司南勺可能指南吗？）

沈括《梦溪笔谈》描述了地磁偏角现象：“方家以磁石磨针锋，则能指南，然常微偏东。”（这真的是地磁偏角现象吗？）

中国有个地方叫磁县。

磁县区位

无独有偶，古希腊也有个地方以“磁”命名——马格尼西亚（Magnesia），这里盛产天然磁石。

马格尼西亚区位

1187年，英国人Alexander Neckam描述了指南针及其在航海导航方面的应用。

皮里格里努斯肖像

1269年，法国人皮里格里努斯出版了磁性研究专著，这部书第一部分定义和描述了磁极，第二部分试图发明磁永动机。

皮里格里努斯的书中的插图

磁永动机

1600年，英国女王的御医吉尔伯特出版了专著《论磁》，这是磁学首次全面完整的研究，吉尔伯特被尊为磁学之父。

吉尔伯特肖像

《论磁》封面

吉尔伯特的一个重要发现是，认为地球是个巨大的磁体。

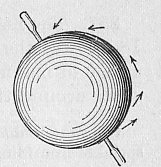
吉尔伯特的地球磁模型

吉尔伯特的首要贡献是磁学方面的工作，但是在电学方面也有很多贡献，研究过导体和绝缘体，英语里电一词（electricity）就是他创造的。他还写了很多科普文章。

女王伊丽莎白一世在1603年去世，仅有的一个遗愿是特许吉尔伯特继续他所着迷的物理研究。可惜，仅几个月后，吉尔伯特死于瘟疫。

电和磁一直是互相独立的现象，但是，1819年，丹麦人奥斯特在课堂上做演示实验时偶然发现电流有磁性。

奥斯特肖像

哥本哈根奥斯特塑像

奥斯特发现电生磁

随后，法国人安培做了多个实验，研究了电流之间的相互作用力，在1820年提出了后来以他的名字命名的安培定律。安培是个神童，12岁就开始学习当时最前沿的数学。

安培肖像

安培定律示意图

磁相互作用力也是通过磁场进行相互作用的。高斯和毕奥与萨伐尔分别独立发现了载流导线的磁感应强度满足的规律，后来被命名为毕奥-萨伐尔定律。毕奥主要研究乐器的振动，萨伐尔主要研究陨石，还发明过热气球。

毕奥肖像

萨伐尔像

磁的基本现象

将磁铁丢如铁屑，再取出时可以发现，磁铁两端吸引的铁屑特别多，即磁性特别强。磁铁有两个磁性特别强的地区，称为磁极。

磁铁的磁极

将条形磁铁或磁针在水平面内自由转动，两磁极分别指向南北方向，两磁极分别称为南极（用S表示）和北极（用N表示）。

指南针

将一根磁铁悬挂起来并能自由转动，用另一磁铁去接近它，可发现，同号磁极互相排斥，异号磁极互相吸引。

磁极的相互作用

奥斯特发现了电流可以使磁针偏转，即电流具有磁效应。

电生磁

磁铁也可以对电流施加作用力。

磁铁也可以对电流施加作用力

电流与电流之间也有相互作用力。

平行电流之间的相互作用

通电螺线管的行为很像磁铁，与磁铁相互作用时，显示出N、S极。

通电螺线管与磁铁相互作用

右手定则确定螺线管极性

安培从螺线管与磁棒之间的相似性，提出磁铁的本源是电流，组成磁铁的最小单元就是环形电流，这些分子环形电流定向排列起来，宏观上就会显示出N、S极来，这就是安培分子环流假说。

安培分子环流假说

这样看来，无论是导线中的电流还是磁铁，它们之间的相互作用的本源都是一样的，即电流，也即运动的电荷，这种相互作用就是磁相互作用，磁相互作用通过磁场进行。

安培定律

电流与电流之间的磁相互作用力满足什么样的规律？

恒定电流只能存在于闭合回路中，而闭合回路的形状和大小和相互位置多种多样，而回路的形状和大小、相互位置都影响二者之间的作用力。我们可以把回路分割成许多无穷小的线元，叫做电流元，把各电流元之间的相互作用得到之后，通过矢量叠加，就可得到两个回路的相互作用力。

把载流回路分割成电流元

安培通过实验得到了电流元之间的作用力：

\begin{equation*} \mathrm d\vec{F}_{12}=k\frac{I_2\mathrm d\vec{l}_2 \times(I_1\mathrm d\vec{l}_1\times \hat{r}_{12})}{r_{12}^2} \end{equation*}

其中，\(I_1\)和\(I_2\)分别为两个回路中的电流，\(\mathrm d \vec{l}\_1\)和\(\mathrm d \vec{l}\_2\)分别为两个回路的线段元，与电流乘在一起就是电流元，线段元的方向即电流的方向，\(r_{12}\)为电流元\(I_1\mathrm d\vec{l}\_1\)到电流元\(I_2\mathrm d\vec{l}\_2\)的距离，\(\hat{r}\_{12}\)为从电流元\(I_1\mathrm d\vec{l}\_1\)指向电流元\(I_2\mathrm d\vec{l} _2\)的单位向量，\(k\)为比例系数，具体值取决于所选的单位制。

力\(\vec{F} _{12}\)的方向不是显而易见的。可通过矢量叉乘右手定则分析。

安培力的方向

两个载流回路的相互作用力：

\begin{equation*} \vec{F}_{12}=k\oint_{L_1}\oint_{L_2}\frac{I_2\vec{l}_2\times(I_1\vec{l}_1\times \hat{r}_{12})}{r_{12}^2} \end{equation*}

课堂练习

1 求平行电流元之间的相互作用力。

可以看出，平行电流元方向相同时，二者之间是吸引力，反平行时，二者之间是排斥力。并容易看出\(\mathrm d\vec{F} _{12}=\mathrm d\vec{F} _{21}\)

平行电流元

2 求垂直电流元之间的相互作用力。

垂直电流元

可以看出，\(\mathrm d\vec{F}\_{12}=0\)，而\(\mathrm d\vec{F}\_{21}\neq 0\)

可见，电流元之间的相互作用力不一定满足牛顿第三定律。但是可以证明两个稳恒电流回路之间安培力满足牛顿第三定律。其实，孤立的稳恒电流元根本不存在，孤立的电流元不可能是稳恒的，而是要随时间变化的，并且会产生一个随时间变化的场，场也具有动量。把电流元与场都看成一个系统，则这个系统的动量守恒，也即牛顿第三定律成立。

参考资料

• 维基百科
• 贾启民《电磁学》
• 赵凯华《电磁学》