理论物理极础10：泊松括号，角动量和对称性

莱尼问：“乔治，我们能用括号钓鱼吗？”
乔治笑答：“能，但只能钓理论鱼。”

力学公理化形式

我们抽象出一套规则来玩泊松括号，而不是计算泊松括号。你可以检验一下这些规则。设 \(A\)、\(B\) 和 \(C\) 都是 \(p\) 和 \(q\) 的函数，根据上一讲的内容，我们可以定义泊松括号：

\begin{equation} \{A,C\} = \sum_i \left ( \frac{\partial A}{\partial q_i}\frac{\partial C}{\partial p_i} - \frac{\partial A}{\partial p_i}\frac{\partial C}{\partial q_i} \right ) \label{eq1} \end{equation}

泊松括号如下性质：

• 反对称性：交换两个函数，泊松括号改变符号：

\begin{equation} \{A,C\} = -\{C,A\} \label{eq2} \end{equation}

特别地，两个同样的函数的泊松括号的运算结果为0：

\begin{equation} \{A,A\} = 0 \label{eq3} \end{equation}

• 线性。线性带来两个性质。第一，如果函数 \(A\) 乘上一个常数 \(k\)，则泊松括号的结果也乘上该常数：

\begin{equation} \{kA,C\}=k\{A,C\} \label{eq4} \end{equation}

第二，两个函数的和 \(A+B\) 与第三个函数 \(C\) 的泊松括号等于 \(A\) 和 \(B\) 分别与 \(C\) 的泊松括号的和：

\begin{equation} \{A+B,C\} = \{A,C\} + \{B,C\} \label{eq5} \end{equation}

• 两个函数的积 \(AB\) 与第三个函数 \(C\)的泊松括号满足如下关系：

\begin{equation} \{AB,C\} = B\{A,C\} + A\{B,C\} \label{eq6} \end{equation}

这个关系可由求导规则得到：

\begin{equation*}
\frac{\partial (AB)}{\partial q} = B \frac{\partial A}{\partial q} + A \frac{\partial B}{\partial q}
\end{equation*}

对 \(p\) 求导也有类似结果。

• 两个 \(q\) 或两个 \(p\) 的泊松括号都为0：

\begin{equation} \begin{split} &\{q_i,q_j\} = 0\\ &\{p_i,p_j\} = 0 \end{split} \label{eq7} \end{equation}

\(q\) 与 \(p\) 的泊松括号未必为0，而是满足如下结果：

\begin{equation} \{q\_i,p\_j\} = \delta\_{ij} \label{eq8} \end{equation}

其中 \(\delta\_{ij}\) 为 克罗内克符号，当 \(i=j\) 时，\(\delta\_{ij}=1\)，当 \(i\neq j\) 时，\(\delta\_{ij}=0\)。

现在我们就可以计算任何泊松括号了。我们可以忘记泊松括号的定义了，方程 \eqref{eq2}、\eqref{eq3}、\eqref{eq4}、\eqref{eq5}、\eqref{eq6}、\eqref{eq7}、\eqref{eq8} 可以作为一套数学形式体系的公理。

比如，我们要计算下式：

\begin{equation} \{q^n,p\} \label{eq9} \end{equation}

为简单起见，系统只有一个\(q\) 和一个 \(p\)。这里先给出答案，然后再证明。答案是：

\begin{equation} \{q^n,p\}=nq^{n-1} \label{eq10} \end{equation}

可以用数学归纳法 证明上式。证明分两步。第一步，假设对于 \(n\)，方程\eqref{eq10}成立，并证明对于 \(n+1\) 也成立。第二步，证明 \(n=1\) 时结论成立。

将 \(n\) 替换为 \(n+1\)，将方程\eqref{eq6}应用于方程\eqref{eq9}，有：

\begin{equation\*} \{q^{n+1},p\}=\{q\cdot q^n,p\}=q\{q^n,p\}+q^n\{q,p\} \end{equation\*}

根据方程\eqref{eq8}，\(\{q,p\}=1\)，上式为：

\begin{equation*} \{q^{n+1},p\}=\{q\cdot q^n,p\}=q\{q^n,p\}+q^n \end{equation*}

应用最后的结论，即\eqref{eq10}，可得：

\begin{equation} \{q^{n+1},p\}=q\{q^n,p\}+q^n=qnq^{n-1}+q^n=(n+1)q^n \label{eq11} \end{equation}

方程\eqref{eq11}正是 \(n+1\) 时的归纳结论。

下一步我们需要证明方程\eqref{eq10}对 \(n=1\)成立。而 \(n=1\) 时，方程\eqref{eq10}为\(\{q,p\}=1\)，这是显然成立的。因此方程\eqref{eq10}得证。

我们下面重新表述这个例子，并得到更深刻的结果。注意到 \(nq^{n-1}\) 正是 \(q^n\) 对 \(q\) 的导数。因此有：

\begin{equation} \{q^n,p\}=\frac{dq^n}{dq} \label{eq12} \end{equation}

如果计算 \(q\) 的任意多项式（甚至是无穷幂级数）与 \(p\) 的泊松括号，可以将方程 \eqref{eq12}应用到多项式的每一项，利用泊松括号的线性性质，将这些项再加起来，则可以证明：

\begin{equation} \{F(q),p\}=\frac{dF(q)}{dq} \label{eq13} \end{equation}

由于任何光滑函数都可以用多项式做任意精确的近似，因此可以证明方程\eqref{13}对 \(q\) 的任意函数都成立。其实，可以有更一般的结论，对于 \(q\) 和 \(p\) 的任意函数，可以证明：

\begin{equation} \{F(q,p),p_i\}=\frac{\partial F(q,p)}{\partial q_i} \label{eq14} \end{equation}

练习1：证明方程\eqref

至此，我们发现了泊松括号的一个新性质：任意函数与 \(p_i\) 的泊松括号等效于求该函数对 \(q_i\) 的偏导数。我们可以从泊松括号的定义证明此结论，但是

函数 \(F(q,p)\) 与 \(q_i\) 的泊松括号会是什么结果？由对称性你可能可以猜到结果，包括fu

\begin{equation} \{F(q,p),q_i\}=\frac{\partial F(q,p)}{\partial q_i} \label{eq15} \end{equation}

练习2：哈密顿方程可以写为 \(\dot{q}=\{q,H\}\)和 \(\dot{p}=\{p,H\}\)，假设哈密顿量为\(H=\frac{p^2}{2m}+V(q)\)，请根据泊松括号公理，导出牛顿方程。

角动量

在第7讲中，我们解释了旋转对称性与角动量守恒之间的关系。这里我们用在 \(x,y\) 平面内运动的质点，做个简要的回顾。无限小转动形式如下：

\begin{equation} \begin{split} &\delta x = \epsilon f_x = -\epsilon y \\ &\delta y = \epsilon f_y = \epsilon x \end{split} \label{eq16} \end{equation}

假设拉格朗日量是不变量，我们可得到一个守恒量

\begin{equation\*} \mathcal{Q}=p_xf_x+p_yf_y \end{equation\*}

小小改变符号，我们称其为角动量\(L\)：

\begin{equation} L=xp_y-yp_x \label{eq17} \end{equation}

现在我们推广至三维空间，方程\eqref{eq16} 仍然适用，但是意义有变，此时表示系统绕 \(z\) 轴旋转。我们可以再补充一个方程，表示绕 \(z\) 轴的旋转不改变 \(z\) 坐标：

\begin{equation} \begin{split} &\delta x = \epsilon f_x = -\epsilon y \\ &\delta y = \epsilon f_y = \epsilon x \\ &\delta z=0 \end{split} \label{eq18} \end{equation}

方程\eqref{eq17} 仍成立，只是我们将其重新解释为角动量的 \(z\) 分量。角动量的其他两个分量同样容易算出，根据方程的变量循环可猜出具体的形式：

\begin{equation\*} \begin{split} &L_z=xp_y-yp_x \\ &L_x=yp_z-zp_y \\ &L_y=zp_x-xp_y \end{split} \end{equation\*}

你可能已经猜到，如果系统对每个轴都有旋转对称性，则矢量 \(\vec{L}\) 的每个分量都是守恒量。

现在我们与角动量有关的泊松括号。比如 \(x\)、\(y\) 和 \(z\) 与 \(L_z\) 的泊松括号：

\begin{equation} \begin{split} &\{x,L_z\} = \{x,xp_y-yp_x\} \\ &\{y,L_z\} = \{y,xp_y-yp_x\} \\ &\{z,L_z\} = \{z,xp_y-yp_x\} \end{split} \label{eq19} \end{equation}

以上各式可以根据泊松括号的定义来计算，也可以通过公理来计算。

练习3：根据泊松括号的定义或公理计算方程\eqref

结果如下：

\begin{equation\*} \begin{split} &\{x,L_z\} = -y \\ &\{y,L_z\} = x \\ &\{z,L_z\} = 0 \end{split} \end{equation\*}

与方程\eqref{eq18}对比，我们会发现一种很有趣的模式。坐标与 \(L_z\) 求泊松括号会重得对 \(z\) 轴的无穷小转动（除了因子 \(\epsilon\)）：

\begin{equation\*} \begin{split} &\{x,L_z\} \sim \delta x \\ &\{y,L_z\} \sim \delta y \\ &\{z,L_z\} \sim \delta z \end{split} \end{equation\*}

其中 \(\sim\) 表示“除了因子 \(\epsilon\)”。

对一守恒量做泊松括号运算可得坐标在与守恒定律相关的对称性下的坐标变换，这不是偶然的。这是一个一般性结论，给我们另一种思考对称性与守恒之间关系的方式。我们讨论这种关系之前，我们讨论一下其他与角动量相关的泊松括号计算。首先，容易将计算推广至 \(L\) 的其他分量，循环一下坐标 \(x\rightarrow y,\quad y\rightarrow z,\quad z\rightarrow x\)，即可得到结果。你会得到6个方程，有无优雅地方法写出所有结果？有！

插播数学：列维-奇维塔符号

如果有一堆符号反复出现，就值得发明一个记号将这一堆符号表示出来。克罗内克符号\(\delta\_{ij}\)就是这样的一个例子。下面我们给出另外例子——列维-奇维塔符号\(\epsilon\_{ijk}\)。与克罗内克符号一样，列维-奇维塔符号的下标\(i,j,k\)也表示空间的三个方向，可以是\(x,y,z\)，有可以是\(1,2,3\)。克罗内克符号有两个取值：1（\(i=j\)时）或者0（\(i\neq j\)时）。\(\epsilon\)符号有三个取值：0，1，或-1，\(\epsilon\_{ijk}\) 的规则比 \(\delta\_{ij}\) 稍复杂。

如果有两个下标相同，\(\epsilon\_{ijk}=0\)，比如 \(\epsilon\_{111}=0\)，\(\epsilon\_{223}=0\)。三个下标中没有相同下标时，\(\epsilon\_{ijk}\) 才不等于0。这有六种情况：\(\epsilon\_{123}\)、\(\epsilon\_{231}\)、\(\epsilon\_{312}\)、\(\epsilon\_{213}\)、\(\epsilon\_{132}\)、\(\epsilon\_{321}\)，前三个值为\(1\)，后三个值为\(-1\)。

这两种情况有何不同？把\(1, 2, 3\) 排在一个圆周上，就像只有3个小时的钟表，见图1。

图1 三个数字 \(1, 2, 3\) 排在一个圆周上

从任何一个数字开始，顺时针走过这三个数字，你会得到 \((123), (231), (312)\)。如果你逆时针走过这三个数字，你会得到\((132), (213), (321)\)。对于顺时针序列，\(\epsilon\_{ijk}=1\)。对于逆时针序列，\(\epsilon\_{ijk}=-1\)。

续论角动量

利用\(\epsilon\) 符号，坐标与角动量分量的泊松括号可写为：

\begin{equation} \{x\_i,L\_j\}=\sum\_k \epsilon\_{ijk}x\_k \label{eq20} \end{equation}

比如你想知道\(\{y,L_x\}\) 的结果，把 \(x,y,z\) 分别定义为 \(1,2,3\)，方程\eqref{eq20}即为：

\begin{equation\*} \{x_2,L_1\}=\epsilon_{213}x_3 \end{equation\*}

由于\(213\)是逆时针序列，因此 \(\epsilon_{213}=-1\)，因此

\begin{equation\*} \{x_2,L_1\}=-x_3 \end{equation\*}

现在我们另一组泊松括号——动量与角动量的泊松括号，利用\(\epsilon\) 符号，易得结果为：

\begin{equation\*} \{p_i,L_j\}=\sum_k \epsilon_{ijk}p_k \end{equation\*}

比如，

\begin{equation\*} \{p_x,L_z\}=-p_y \end{equation\*}

容易注意到，\(p\) 与 \(L\) 的泊松括号与 \(x\) 与 \(L\) 的泊松括号，形式完全一样，这很有意思，在坐标经过旋转之后，\(p\) 和 \(x\) 的变换是一样的。正如经过绕\(z\)轴旋转之后，\(\delta x \sim y\)，\(p_x\) 的变换量也正比于\(-p_y\)。

这里面的水深着呢。坐标旋转之后，要计算任何一个量的变化量，只需计算该量与角动量的泊松括号。对于绕第 \(i\) 轴的旋转，有：

\begin{equation} \delta F=\{F,L_i\} \label{eq21} \end{equation}

角动量是旋转操作的生成元。

我们还会再回到这个主题，还有对称变换、泊松括号与守恒量之间的密切联系。我们先说明一下，如何用泊松括号分析和解决问题。

转子和进动

我们还没有计算角动量三个分量之间的泊松括号。自身与自身的泊松括号总是0，但是\(L\)不同分量之间的泊松括号不是0。考虑

\begin{equation\*} \{L_x,L_y\}=\{yp_z-zp_y,zp_x-xp_z\} \end{equation\*}

根据泊松括号定义，或者根据力学公理，我们都可以得到：

\begin{equation\*} \{L_x,L_y\}=L_z \end{equation\*}

你不妨试一下。

一般关系可以通过列维-奇维塔符号写出来：

\begin{equation} \{L_i,L_j\}=\sum_k \epsilon_k L_k \label{eq22} \end{equation}

非常漂亮的形式。我们能做些什么呢？为了见识一下方程\eqref{eq22}等关系的威力，我们考虑外太空一个快速转动的小球，我们称其为转子。在任意时刻，转子都有一个转动轴，角动量即沿转轴的方向。如果转子不受任何外在影响，它的角动量守恒。

假设转子带有电荷。由于转子在高速旋转，它就像一个南北极沿着转轴的电磁体。偶极的大小正比于转速，更好的说法是正比于角动量。如果不把转子置于磁场中，这两种说法没有什么不同。如果将带电转子置于磁场\(\vec{B}\)中，就会有一个与\(\vec{L}\) 与 \(\vec{B}\)不平行相关的能量项，见图2。

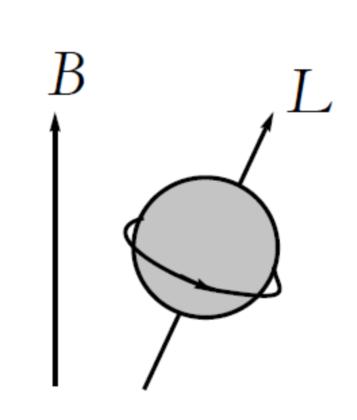
图2 转子取向与外磁场方向之间的夹角

这个能量正比于两个矢量夹角的余弦值，也正比于两个矢量的大小的积，即正比于两个矢量的点积：

\begin{equation} H\sim \vec{B}\cdot \vec{L} \label{eq23} \end{equation}

这里用\(H\)表示能量，后面我们会看出，这就是系统的哈密顿量。

假设外磁场的方向沿\(z\)轴，于是\(H\)正比于\(\vec{L}\)的\(z\)分量。把磁场强度、电量、球半径等各种常量归到一个常量\(\omega\)里，这样\(H\)可写为如下形式：

\begin{equation} H=\omega L_z \label{eq24} \end{equation}

我们先暂停一下，想想我们在做什么。很明显，如果没有外磁场，系统具有旋转对称性，转动转子的轴，系统能量不变。但是加上外磁场，转动就有参照物了，因此转动对称性被破坏。方程\eqref{eq23}和\eqref{eq24}表示旋转不对称性。这会带来什么后果？答案很明显：角动量不再守恒——没有对称性就没有守恒。这意味着转动的方向将随时间而变。如何变？

你可以试着猜下答案。转子是磁体，直觉告诉我们，角动量将向着\(\vec{B}\)来回摆动，像单摆一样。这是错的，如果小球转动很快的话。真实的情况是，角动量将会绕着磁场进动，像陀螺仪绕着引力场那样运动。下面我们用泊松括号来得到矢量\(\vec{L}\)的运动方程。

首先，我们还记得任何一个量的时间导数是该量与哈密顿量的泊松括号。把这个规则应用于\(\vec{L}\)的分量，有：

\begin{equation*} \begin{split} &\dot{L}_z=\{L_z,H\} \\ &\dot{L}_x=\{L_x,H\} \\ &\dot{L}_y=\{L_y,H\} \end{split} \end{equation*}

带入方程\eqref{eq24}，

\begin{equation*} \begin{split} &\dot{L}_z=\omega \{L_z,L_z\} \\ &\dot{L}_x=\omega \{L_x,L_z\} \\ &\dot{L}_y=\omega \{L_y,L_z\} \end{split} \end{equation*}

现在你就能看出点端倪了。即使你对转子的材料、电荷的分布等等一无所知，你也能解出此问题，因为我们知道\(\vec{L}\)各分量的泊松括号。\(L_z\) 与自己的泊松括号为0，有：

\begin{equation*} \dot{L}_z=0 \end{equation*}

\(\vec{L}\)的\(z\)分量不随时间变化，这就排除了\(\vec{L}\)相对\(\vec{B}\)来回摆动这一想法。

根据方程\eqref{eq22}可得\(\dot{L}\_x\)和\(\dot{L}\_y\)分别满足如下方程：

\begin{equation*} \begin{split} &\dot{L}_x=-\omega L_y \\ &\dot{L}_y=\omega L_x \end{split} \end{equation*}

这与\(x,y\)平面上绕着原点做匀速圆周运动的矢量的方程是一样的。换言之，\(\vec{L}\) 绕着磁场进动。这就是泊松括号的魔力，只知道哈密顿量正比于\(\vec{B}\cdot \vec{L}\)这一点信息，就解决了问题。

对称与守恒

再回到方程\eqref{eq21}，这个方程的意义是，在旋转操作下，任何一个物理量的变化都正比于该物理量与\(L_i\)的泊松括号。\(L_i\)恰巧就是一个守恒量，因为\(L_i\)是旋转操作下的不变量。这个联系很有意思，这个联系具有一般性吗？我们再另外举一些例子。考虑一个沿直线运动的质点，如果存在平移不变性，那么动量守恒。现在我们算一下\(x\)的任一函数与\(p\)的泊松括号：

\begin{equation\*} \{F(x),p\}=\frac{d F}{d x} \end{equation\*}

在一个无限小的平移 \(\epsilon\) 下，\(F(x)\)的变化量是多少？答案是：

\begin{equation\*} \delta F=\epsilon \frac{d F}{d x} \end{equation\*}

即

\begin{equation\*} \delta F=\epsilon \{F(x),p\} \end{equation\*}

另外一个例子：如果系统具有时间平移不变性，哈密顿量守恒。在时间平移操作下，物理量的改变量是多少？你已经猜到了——该物理量与\(H\)的泊松括号。

我们下面看看泊松括号与守恒量之间的这一联系是否具有一般性。令\(G(q,p)\)为系统的生成元，生成相空间各点的微小位移，生成元定义如下：

\begin{equation} \begin{split} &\delta q_i= \{q_i,G\} \\ &\delta p_i= \{p_i,G\} \end{split} \label{eq25} \end{equation}

其中\(\delta q_i,\delta p_i\)为相空间各点平移量。

\(G\)产生的变换可能是系统的一个对称操作，也可能不是。什么意思？意思是不管你从何处开始，\(G\)产生的变换都不会改变系统的能量。换言之，如果在\(G\)产生的变换下\(\delta H=0\)，我们称此变换为一种对称操作，即变换为对称操作的条件是：

\begin{equation} \{H,G\}=0 \label{eq26} \end{equation}

方程\eqref{eq26}还有另一种解读。改变泊松括号中的两个函数的次序只会改变结果的符号，那么方程\eqref{eq26}还可写为：

\begin{equation} \{G,H\}=0 \label{eq27} \end{equation}

这正是\(G\) 为守恒量的条件。我们可以说：告诉我们在\(G\)产生的变换下\(H\)如何变化的泊松括号同时告诉我们\(G\)如何随时间变化。