电磁学讲义3:电场
简史
在静电学里,电作用力可看做瞬时的超距作用,但是超距作用的观点有点神秘主义,为大多数科学家所难以接受,尽管同样的观点包含于牛顿的万有引力定律中。法拉第注意到,铁屑在磁棒周围形成确定的曲线,法拉第称此曲线为力线。法拉第进而猜想,电荷也对应有力线,他认为,每个正电荷从自身发出力线,力线最终终止于负电荷。法拉第的力线现在称为电场线。
若一个正电荷与法拉第的力线(电场线)相遇,该物体受到沿电场线切线方向的力的作用,某处的电场线密度较另一处的密度大时,该物体在该处受到的力比别处的力大。
法拉第这种直观图像很快就被人们接受了,由此,人们分析问题的注意力从单个电荷转化为电场的整体上来。法拉第这种图像提供了一种不用数学工具来定量描述电场的。但是对于比较复杂的电荷分布的电场的分析,数学工具还是必不可少的。1845年,开尔文第一个尝试用数学描述法拉第的力线(参:Buchwald, J.Z. (1977). "William Thomson and the mathematization of Faraday's electrostatics". Historical Studies in the Physical Sciences 8: 101–136. doi:10.2307/27757369.)自1855年开始,麦克斯韦开始用数学方法描述法拉第的力线,发展了电场、磁场和电磁场的概念,最终取得完全的成功。
图为法拉第
电场
我们考虑两个带正电的物体A和B,设B所带电荷为\(q_0\),受到的静电力为 \(\vec {F}\_0\),如图a。对二者之间的静电力有两种思考方法,一是认为静电力是超距力,像万有引力那样。带电物体可以不借助任何媒介,通过空间直接相互作用。另外一个思考方式是,二者之间的相互作用力通过两个阶段产生的。首先,A上的电荷会改变A周围空间的性质,B上的电荷能够感受到空间新的性质,对空间的新的性质就会有个响应,这个响应就是静电力 \(\vec {F}\_0\)。
电场的概念是很简单的:电荷在空间产生电场,处于电场中的电荷就会感受到一个力。
下面我们详细说一下这个过程。首先只考虑物体A,把点电荷B移走,它所在的位置标记为\(P\),如图b所示,物体A由于带电,就会改变空间的性质,我们称为建立一个电场,A周围任何一点都有电场,\(P\)点当然不例外,即便这里没有电荷存在,也有电场的存在,因为电场是\(A\)的电荷产生的。现在把点电荷B放在\(P\),B就会受到一个力\(\vec{F}_0\),这个力我们认为是\(P\)点处的电场直接施加的,力的根本来源还是物体A是的电荷,电场只是A和B之间相互作用的媒介。B的电荷当然也要建立一个电场,B的电场对A施加力\(-\vec{F}\_0\)。注意一点,电荷产生的电场对自身不施加力的作用。
要在实验上看空间某点是否有电场,可以把一个很小的带电体放在那里,看带电体是不是受到有力的作用,如果受到力的作用,就说明那里有电场,如图c所示。我们引入的这个小带电体叫做试探电荷,试探电荷要充分小,可以看做点电荷,这样才可以确定空间各点的电场。试探电荷的电量\(q_0\)也应该充分小,以免改变了原来的电荷分布。

图 带电物体在自身周围产生电场
力是一个矢量,电场也是一个矢量,电场可定义为试探电荷所受的静电力与试探电荷的电量的比值,即空间某点处的电场为该点处单位电荷所受到的静电力,即
\begin{equation*} \vec{E}=\frac{\vec{F}_0}{q_0} \end{equation*}
在国际单位制中,电场的单位为\(\mathrm{N/C}\)。电场的方向与正电荷所受电场力的方向一致,与负电荷所受电场力的方向相反。

图 静电力与电场的方向
如果已知空间各点处的电场,那么也可以知道空间某点处电荷所受的力:
\begin{equation*} \vec{F}_0=q_0 \vec{E} \end{equation*}
需要注意的是,上式只适用于试探电荷。试探电荷在各点受到的静电力可以是不一样的,即各点的电场可以是不一样的。因此,上式只适用于点电荷。如果带电体比较大,带电体上各点处的电场可能会不同,带电体所受的合静电力可能会非常复杂。

鲨鱼靠感知猎物肌肉收缩产生的电场来捕获猎物,见Scientific American 297, 74 - 81 (2007)
点电荷的电场
我们现在求点电荷\(q\)产生的电场。点电荷\(q\)所在的位置\(O\)点处为源点,求距离\(q\)电荷\(r\)处某一点\(P\)处(此点称为场点)的电场。设想在\(P\)点处放置一个试探电荷,其电量为\(q_0\),根据库仑定律,试探电荷的力为
\begin{equation*} \vec{F}_0=\frac{1}{4\pi\varepsilon_0}\frac{qq_0}{r^2} \hat{r} \end{equation*}
式中\(\hat{r}\)为沿\(\overline{OP}\)方向的单位矢量,\(P\)点处的场强为
\begin{equation*} \vec{E}=\frac{\vec{F}_0}{q_0}=\frac{1}{4\pi\varepsilon_0}\frac{q}{r^2} \hat{r} \end{equation*}
上式对正负电荷都是适用的。对于正电荷,\(q>0\),\(\vec{E}\) 沿 \(\hat{r}\) 方向,即远离电荷的方向。对于负电荷,\(q<0\),\(\vec{E}\) 沿 \(-\hat{r}\) 方向,即指向电荷的方向。由于场点 \(P\) 是任意的,所以我们已经得到了点电荷\(q\) 的电场的空间分布。

点电荷在\(P\)点处场强
矢量用箭头表示,箭头的指向是该点场强的方向,箭头的长短表示场强的大小。从这里我们可以看出,描绘电场的分布不能用单个矢量表示,而是要空间每个点上都要有一个矢量,这样的矢量的总体叫做矢量场。

点电荷的电场是矢量场
电场的叠加原理
由多个点电荷\(q_1,q_2,\ldots\) 组成的电荷系统,对空间某一点\(P\) 处试探电荷\(q_0\)的力为
\begin{equation*} \vec{F}_0 = \vec{F}_1 + \vec{F}_2 + \vec{F}_3 + \ldots \end{equation*}
电场为
\begin{equation*} \begin{split} \vec{E}=&\frac{\vec{F}_0}{q_0}=\frac{\vec{F}_1}{q_0} + \frac{\vec{F}_2}{q_0} + \frac{\vec{F}_3}{q_0} + \ldots \\ =& \vec{E}_1 + \vec{E}_2 + \vec{E}_3 + \ldots \end{split} \end{equation*}
式中 \(\vec{E}\_1,\vec{E}\_2,\ldots\) 分别代表点电荷\(q_1,q_2,\ldots\) 单独存在时在空间同一点的场强,\(\vec {E}\) 代表这些电荷同时存在时在该点的总电场。这就是电场的叠加原理:
点电荷系统所产生的电场在某点的电场等于各点电荷单独存在时所产生的电场在该点电场强度的矢量和。
例 电偶极子的电场
由一对靠得很近的等量异号电荷构成的体系称为电偶极子。比如绝缘体中的原子在带电体附近,正负电荷分布中心产生微小的偏离,形成电偶极子。
考虑一对相距 \(l\) 的等量异号电荷 \(+q\) 和 \(-q\) 组成的电偶极子,描述电偶极子性质的物理量是电偶极矩,其定义为电量 \(q\) 和 \(l\) 的乘积,电偶极矩是矢量,方向是从负电荷指向正电荷,电偶极矩为 \(\vec{p}=q\vec{l}\)。
现在我们求一下两电荷延长线上一点 \(P\) 处和中垂面上一点 \(P'\) 处的电场强度。
(i) 求两电荷延长线上一点 \(P\) 处的电场强度

以电偶极子中心为坐标原点,以电偶极矩方向为正方形建立 \(x\) 轴。设 \(P\) 点坐标为 \(x\),正负电荷在 \(P\) 点处的电场分别为 \(\vec{E}_+\) 和 \(\vec{E}_-\),则电偶极子在 \(P\) 点处产生的电场为
\begin{equation*} \begin{split} \vec{E}=&\vec{E}_+ + \vec{E}_- = \frac{1}{4\pi\varepsilon_0}\frac{q}{\left (x-\frac{l}{2}\right )^2}\hat{i} +\frac{1}{4\pi\varepsilon_0}\frac{-q}{\left (x+\frac{l}{2}\right )^2}\hat{i} \\ =& \frac{q}{4\pi\varepsilon_0}\left [\frac{1}{\left (x-\frac{l}{2}\right )^2}-\frac{1}{\left (x+\frac{l}{2}\right )^2} \right ]\hat{i} \\ =& \frac{q}{4\pi\varepsilon_0x^2}\left [\frac{1}{\left (1-\frac{l}{2x}\right )^2}-\frac{1}{\left (1+\frac{l}{2x}\right )^2} \right ]\hat{i}\\ =& \frac{q}{4\pi\varepsilon_0x^2}\frac{2l/x}{\left [ 1-\left ( \frac{l}{2x} \right )^2 \right ]^2}\hat{i} \end{split} \end{equation*}
当 \(l\ll x\) 时,上式为
\begin{equation*} \vec{E}=\frac{ql}{2\pi\varepsilon_0x^3}\hat{i}=\frac{\vec{p}}{2\pi\varepsilon_0x^3} \end{equation*}
(ii)求两电荷中垂面上一点 \(P'\) 处的电场强度
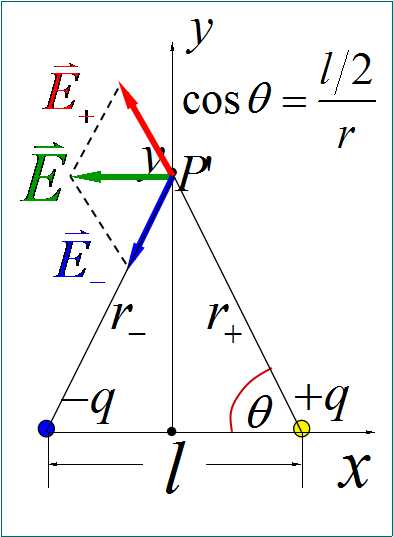
\(P'\)点距离两个电荷的距离相等,\(r_+=r_-=r\)。两个电荷在 \(P'\) 点产生的电场的大小相等,
\begin{equation*} E_+ = E_- = \frac{1}{4\pi\varepsilon_0}\frac{q}{r^2} \end{equation*}
电偶极子在 \(P'\) 点处产生的场强为:
\begin{equation*} \vec{E}=\vec{E}_+ + \vec{E}_- \end{equation*}
由对称性知,\(\vec{E}\) 的 \(y\) 分量为0,即\(\vec{E}\) 方向沿 \(x\) 轴负方向,
\begin{equation*} \begin{split} \vec{E}=&E_x \hat{i} = -2E_+\cos\theta \hat{i} = -E_+\frac{l}{r} \hat{i} \\ =& -\frac{1}{4\pi\varepsilon_0}\frac{ql}{r^3} \hat{i} =-\frac{1}{4\pi\varepsilon_0}\frac{ql}{\left[y^2+\left (\frac{l}{2}\right )^2\right ]^{3/2}} \hat{i}\\ =& -\frac{ql}{4\pi\varepsilon_0y^3}\frac{1}{\left[1+\left (\frac{l}{2y}\right )^2\right ]^{3/2}} \hat{i} \end{split} \end{equation*}
当 \(l\ll y\) 时,上式为
\begin{equation*} \vec{E}=-\frac{ql}{4\pi\varepsilon_0y^3}\hat{i}=-\frac{\vec{p}}{4\pi\varepsilon_0y^3} \end{equation*}
再由习题1-8结果,距离电偶极子远处,\(l\ll r\),电偶极子的电场强度 \(E\sim \frac{1}{r^3}\)
作业
习题 1-8、1-11
参考资料
- 《力学以外的世界》
- Chapter 3 of Electricity, Magnetism, and Light
- Young and Freedman, University Physics 13th Edition
- 赵凯华《电磁学》



 浙公网安备 33010602011771号
浙公网安备 33010602011771号