理论物理极础8：哈密顿力学和时间平移不变性

酒吧的伙计边喝饮料边读报，这时莱尼和乔治进来了。“酒保，你在读什么呢？”
伙计抬头看了下莱尼，说：“报上引用爱因斯坦的话：‘精神错乱就是一遍又一遍地重复作同一件事，而期待会有不同的结果。 ’你如何理解这句话？”
莱尼想了想，说：“就像我来这里，每次都点辛辣的食物，结果得了胃病？”
酒保笑了：“就是这意思。你都开始懂爱因斯坦了。”

时间平移对称性

你可能想知道能量守恒与对称性是不是有关系。确实有关系，但是又与我们在第7讲中讲的又不太一样。第7讲中所有对称性的例子都与坐标\(q_i\)平移有关。比如，平移对称性是将所有质点的笛卡尔坐标都同时平移相同的量，系统不发生任何变化。与能量守恒相关的对称性不是坐标平移，而是时间平移。

想象一个封闭系统的实验，不受任何外界影响。实验在\(t_0\)时刻开始，从一定初始条件开始演化，过一定时间后，看看得到的结果。然后晚些时候，重复实验，保持初始条件不变，持续时间不变，唯一不同的是起始时刻，推迟到\(t_0+\Delta t\)。你会猜想到实验结果应该会完全一样，时间平移量\(\Delta t\)不会带来任何变化。对于具有这样性质的系统，我们称其具有时间平移不变性。

不是所有系统都具有时间平移不变性。比如，我们生活在一个一直在膨胀的宇宙里。宇宙的膨胀效应在通常的实验条件下通常是可以忽略的，但是如果实验足够精确的话，晚一会儿做的实验和前面做的实验，结果会有细微差别。

下面我们说一个更接近现实的例子。考虑一个在磁场中运动的带电粒子。如果磁场是恒磁场，粒子运动是时间平移不变的。但是如果产生磁场的电流慢慢增大，粒子如果在同样的初始条件但在不同的时刻开始运动，我们就会得到不同的结果。粒子的运动就不是时间平移不变的。

时间平移对称性的是否存在如何体现在拉格朗日力学里？答案很简单，看拉格朗日量是否显含时间，说得清楚一点，看拉格朗日量的值随时间而变是否仅仅是通过坐标和速度的变化。如果是，则拉格朗日量隐含时间，如果否，则拉格朗日量显含时间。显含时间意思是拉格朗日量的函数形式里直接就有时间。比如谐振子的拉格朗日量：

\[L=\frac{1}{2}\left (m\dot{x}^2+kx^2\right ) \]

如果\(m\)和\(k\)不随时间改变，上述拉格朗日量就是时间平移不变的。

如果弹簧常数\(k\)因为某种原因随时间变化，比如在一个有变化磁场的环境里，变化的磁场对弹簧里的原子有作用，这种作用会改变弹簧常数。在这样的情况，拉格朗日量为

\[L=\frac{1}{2}\left [m\dot{x}^2+k(t)x^2\right ] \]

这个拉格朗日量就是显含时间的。一般的拉格朗日量可写为
\begin{equation}
L=L(q_i,\dot{q}_i,t)
\label{eq1}
\end{equation}

拉格朗日量的时间依赖性是源于体系的控制参数随时间的变化。

由此，我们可以给出时间平移对称性的数学判据：拉格朗日量不显含时间，则系统是时间平移不变的。

能量守恒

现在我们考虑拉格朗日量（方程\eqref{eq1}）的值如何随着系统演化而变化。拉格朗日量\(L\)的时间依赖性有三个来源。第一和第二个来源是坐标\(q\)和速度\(\dot{q}\)的时间依赖性。如果时间时间依赖性的来源仅此而已，则有

$$\frac{dL}{dt}=\sum_i\left (\frac{\partial L}{\partial q_i}\dot{q}_i+\frac{\partial L}{\partial \dot{q}_i}\ddot{q}_i \right )$$

如果拉格朗日量表达式里就显含时间，拉格朗日量对时间的微分就多出一项：

\begin{equation} \frac{dL}{dt}=\sum_i\left (\frac{\partial L}{\partial q_i}\dot{q}_i+\frac{\partial L}{\partial \dot{q}_i}\ddot{q}_i \right )+\frac{\partial L}{\partial t} \label{eq2} \end{equation}

我们逐一看看方程\eqref{eq2}中各项。由欧拉-拉格朗日方程，方程\eqref{eq2}求和号中第一项可写为：

$$\frac{\partial L}{\partial q_i}\dot{q}_i=\dot{p}_i\dot{q}_i$$

第二项变为

$$\frac{\partial L}{\partial \dot{q}_i}\ddot{q}_i = p_i\ddot{q}_i$$

以上各项再带入方程\eqref{eq2}，得：

$$\frac{dL}{dt}=\sum_i \left (\dot{p}_i\dot{q}_i+p_i\ddot{q}_i \right ) + \frac{\partial L}{\partial t}$$

上式中的求和项可以简化，得如下恒等式：

$$\sum_i \left (\dot{p}_i\dot{q}_i+p_i\ddot{q}_i \right ) = \frac{d}{dt}\sum_i p_i \dot{q}_i$$

于是，得

\begin{equation} \frac{dL}{dt}=\frac{d}{dt}\sum_i p_i \dot{q}_i+\frac{\partial L}{\partial t} \label{eq3} \end{equation}

由上式可注意到，即使拉格朗日量\(L\)不显含时间，拉格朗日量也有时间依赖性，即通过第一项 \(\frac{d}{dt}\sum_i p_i \dot{q}_i\) 随时间变化。也就是说，拉格朗日量不守恒。

观察方程\eqref{eq3}，可以看到一些有意思的东西。我们定义一个新的量\(H\)：

\begin{equation} \sum_i p_i \dot{q}_i-L=H \label{eq4} \end{equation}

则方程\eqref{eq3}可变为如下简单的形式：

\begin{equation} \frac{d H}{dt}=-\frac{\partial L}{\partial t} \label{eq5} \end{equation}

得到方程\eqref{eq5}的步骤有点复杂，但是这个结果很简单。只有当拉格朗日量显含时间的时候，\(H\)才随时间变化。更有趣的事情，如果系统是时间平移不变的，则量\(H\)守恒。

量\(H\)叫做哈密顿量，你可能已经猜到，它很重要，因为它是系统的能量，当然还有其他的原因。更重要的是，哈密顿量是力学一个新的形式理论——哈密顿力学的核心。眼下，我们还是从一个简单的例子，理解一下哈密顿量的意义。考虑势场中运动的一个质点，其拉格朗日量为：

\begin{equation} L=\frac{1}{2}m\dot{x}^2-V(x) \label{eq6} \end{equation}

正则动量就是通常的动量：

\begin{equation} p=m\dot{x} \label{eq7} \end{equation}

将方程\eqref{eq6}和\eqref{eq7}带入方程\eqref{eq4}，得哈密顿量：

\begin{equation*} \begin{split} H& = (m\dot{x})\dot{x}-\frac{1}{2}m\dot{x}^2+V(x)\\ & = m\dot{x}^2-\frac{1}{2}m\dot{x}^2+V(x)\\ & = \frac{1}{2}m\dot{x}^2+V(x) \end{split} \end{equation*}

可见，\(H\)正是能量，动能加上势能。

对于一般情况，拉格朗日量是动能减去势能，哈密顿量为：

\begin{equation*} \begin{split} H& = p\dot{q}-T+V\\ & = T+V \end{split} \end{equation*}

有些系统的拉格朗日量会比较复杂，不能很明显的写为\(T-V\)。对于这样的情况，可能无法清楚地分出动能和势能。但不管怎样，构建哈密顿量的规则不变。系统的能量的一般定义是：
能量等于哈密顿量。
并且，如果拉格朗日量不显含时间，能量\(H\)守恒。

如果拉格朗日量显含时间，根据方程\eqref{eq5}，哈密顿量不守恒。能量不守恒，会怎么样呢？我们通过一个例子来说明一下。一个带电粒子，带有单位电量的电荷，在一个平板电容器之间运动，其实就是在一个匀强电场 \(\epsilon\) 中运动。（这里我们用 \(\epsilon\) 表示电场，而不是用通常的符号\(E\)，是为了避免与能量的符号混淆。）现在你不需要管电场是什么，你只需要知道的是，电容器产生一个势能 \(\epsilon x\)。拉格朗日量为：

\[L=\frac{1}{2}m\dot{x}^2-\epsilon x \]

只要电场是恒定的，能量就是守恒的。但是，如果电容器正在充电，那么 \(\epsilon\) 就是逐渐增大的，此时拉格朗日量就是显含时间的：

\[L=\frac{1}{2}m\dot{x}^2-\epsilon(t) x \]

这种情况下，带电粒子的能量就不守恒了，能量的变化率为：

\[\frac{dH}{dt}=\frac{d\epsilon}{dt}x \]

增加的能量来自哪里呢？答案是来自给电容器充电的电池。这里不讲细节，只讲重点，如果系统只包括电容器中间的那个带电粒子，系统的能量不守恒，因为这只是包括电容器和电池在内的一个更大的系统的一部分，电容器和电池也是有能量的。

我们考虑下这整个实验，包括电池、电容器和带电粒子。最开始，电容器不带电，粒子静止在电容器极板间某处。某个时刻，接通电路，电流流向电容器，带电粒子感受到一个随时间变化的电场。实验最后的结果，电容器带上电荷，带电粒子运动起来。

再过一个小时后我们再做整个实验会怎么样呢？当然完全一样。换言之，整个系统是时间平移不变的，所以把电池、电容器和带电粒子看做一个系统，能量是守恒的。

但是，在很多问题里，把系统分成各个部分来研究会非常方便。在这样的情况下，如果系统里除你的研究对象之外的部分随时间变化，那么你的研究对象的能量就不守恒。

相空间和哈密顿方程

哈密顿量不仅仅是能量，还具有更深层的意义：哈密顿量是经典力学的全新的理论形式的基础，在量子力学里，它会更重要。

在拉格朗日力学里，我们关注的是系统的构型空间轨迹，轨迹用坐标\(q(t)\)描述。运动方程是二阶微分方程，所以只知道初始坐标是不够的，还需要知道初始速度。

哈密顿力学关注的是相空间。在哈密顿力学里，坐标\(q_i\)和速度\(p_i\)地位完全一样，\(q_i\)和速度\(p_i\)构成的空间即是相空间。系统的运动由相空间中的轨迹描述，数学上讲，由函数集合\(q_i(t)\)和\(p_i(t)\)来描述。所以，相空间的维数是构型空间维数的2倍。

维数增加一倍有什么好处？答案是，运动方程变成一阶微分方程，通俗点说，只要知道相空间中的初始点，就可以确定系统的未来。

构建哈密顿力学的第一步是消除所有的\(\dot{q}\)，代之以\(p\)。对于通常的笛卡尔坐标系里的质点，动量和速度说的基本是一件事情，只差了个因子质量。我们以沿直线运动的质点为例来说明如何构建哈密顿力学。我们有这样两个方程：

\begin{equation} \begin{split} & p = m\dot{x}\\ & H = \frac{1}{2}m\dot{x}^2+V(x) \end{split} \label{eq8} \end{equation}

速度用\(p/m\)替换，哈密顿量就变成\(p\)和\(x\)的函数：

\[H=\frac{p^2}{2m}+V(x) \]

\(H\)对\(x\)的偏导数为\(\frac{dV}{dx}\)，正是负的力，因此运动方程（\(F=ma\)）为如下形式

\begin{equation}
\dot{p}=-\frac{\partial H}{\partial x}
\label{eq9}
\end{equation}

前面已经提到，在哈密顿力学里，坐标和动量地位完全一样，由此，你可能会猜到还有一个与方程\eqref{eq9}类似的方程，只是把\(p\)和\(x\)换一下位置。几乎如此，只是差那么一点点。正确的方程是：

\begin{equation}
\dot{x}=\frac{\partial H}{\partial p}
\label{eq10}
\end{equation}

你可以由方程\eqref{eq8}验证一下。

现在我们就得到了运动方程，简洁对称，只是不是一个方程，而是两个一阶微分方程

\begin{equation} \begin{split} & \dot{p}=-\frac{\partial H}{\partial x}\\ & \dot{x}=\frac{\partial H}{\partial p} \end{split} \label{eq11} \end{equation}

以上就是直线运动的质点的哈密顿方程。我们现在推导一般系统的哈密顿方程。先从哈密顿量开始：

\[H=H(q_i,p_i) \]

类比方程\eqref{eq11}，有

\begin{equation} \begin{split} & \dot{p}_i=-\frac{\partial H}{\partial q_i}\\ & \dot{q}_i=\frac{\partial H}{\partial p_i} \end{split} \label{eq12} \end{equation}

在相空间的每一个维度上，都对应一个一阶微分方程。

我们说一下该方程组与第1讲的关系。本书第一章描述了决定论性定律如何确定未来。方程\eqref{eq12}就可以确定系统的未来：如果你知道系统的哈密顿量，以及任意时刻的所有坐标和动量，哈密顿方程就能告诉你下个瞬时的所有坐标和动量。如此进行下去，你就能确定相空间的轨迹。

谐振子的哈密顿力学

谐振子是物理里面最重要的简单系统。某自由度偏离平衡位置之后，然后在平衡位置附近振动，各种各样的体系都有这样的振动，所有这样的振动都可以用谐振子描述。我们考虑一个自由度\(q\)，势能\(V(q)\)有一个极小值点，不失一般性，我们假设极小值点在\(q=0\)处。极小值点附近的势能可用二次函数来近似：

\begin{equation}
V(q)=V(0)+cq^2
\label{eq13}
\end{equation}

其中\(V(0)\)和\(c\)都为常数。没有\(q\)的一次项，是因为导数\(\frac{dV}{dq}\)在极小值点必须等于0。我们也可以略去\(V(0)\)这一项，因为势能加上一个常数项对系统没有任何影响。

方程\eqref{eq13}并不具有一般性，\(V\)可以含有\(q\)的高阶项，如\(q^3\)、\(q^4\)等。只要系统偏移\(q=0\)处的程度非常小，这些高阶项都可以忽略。这可适用于各种系统：弦、摆、声波、电磁波，等等。

谐振子的拉格朗日量可写成如下特殊形式：

\begin{equation}
L=\frac{1}{2\omega}\dot{q}^{2+\frac{\omega}{2}q}2
\label{eq14}
\end{equation}

这个拉格朗日量只含一个常数 \(\omega\) 。

练习1：从拉格朗日量\(\frac{m\dot{x}^2}{2}-\frac{kx^2}{2}\)出发，证明做变量替换\(q=(km)^{1/4}x\)，可得如方程\eqref{eq14}形式的拉格朗日量。写出\(k\)、\(m\)和\(\omega\)之间的关系。

练习2：方程\eqref{eq14}所对应的哈密顿量。

方程\eqref{eq14}所对应的哈密顿量具有非常简单的形式：

\begin{equation}
H=\frac{\omega}{2}(p^2+q2)
\label{eq15}
\end{equation}

要得到这么简单的哈密顿量，我们需要把\(x\)变成\(q\)，这就是练习1所做的事情。

哈密顿力学的一大特征是\(q\)和\(p\)是对称的，而二者在谐振子的哈密顿量里几乎完全对称，仅有的不对称来自方程\eqref{eq12}中的负号。将方程\eqref{eq15}带入方程\eqref{eq12}，得

\begin{equation} \begin{split} & \dot{p}=-\omega q \\ & \dot{q}=\omega p \end{split} \label{eq16} \end{equation}

我们把哈密顿力学得到的这两个方程与拉格朗日力学得到的欧拉-拉格朗日方程做下比较。由方程\eqref{eq14}可得欧拉-拉格朗日方程：

\begin{equation}
\ddot{q}=-\omega^2q
\label{eq17}
\end{equation}

首先，欧拉-拉格朗日方程只有一个，而哈密顿方程有两个。第二，欧拉-拉格朗日方程是二阶的，而哈密顿方程是一阶的。两个一阶的哈密顿方程与一个二阶欧拉-拉格朗日方程是等价的。方程\eqref{eq16}中的的第二个方程对时间在求一次导数，得：

\[\ddot{q}= \omega \dot{p} \]

再由方程\eqref{eq16}中的第一个方程，把上式中的 \(\dot{p}\) 换成\(-\omega q\)，我们就得到方程\eqref{eq17}，欧拉-拉格朗日方程。

两种理论形式，哪个更好？看你的感觉了。但是先别忙着下结论，等学完相对论和量子力学，拉格朗日量和哈密顿量的意义才会变得完全清晰。

我们再回到方程\eqref{eq16}。我们习惯于在构型空间思考问题。谐振子系统沿着某个轴往复运动。谐振子系统是我们慢慢习惯相空间思考问题的一个很好的起点。谐振子的相空间是二维的。容易看出，谐振子的相空间轨迹是以原点为圆心的同心圆。道理很简单，回到哈密顿量表达式，方程\eqref{eq15}，哈密顿量，也就是能量，是守恒的，\(q^2+p^2\)是与时间无关的常数。即到相空间原点的距离是不变的，相点沿着半径固定的圆移动，并且角速度恒定为\(\omega\)。更有意思的是，所有轨道对应的角速度都相等，与谐振子的能量无关。把相点的圆周运动投影到横坐标\(q\)轴上，如图1所示，不出所料，相点沿\(q\)轴做往复运动，这正是振动的特点。但是，相空间二维的圆周运动才是振动的全面描述。把轨迹投影到纵坐标\(p\)轴，可以看出，动量也在振动。

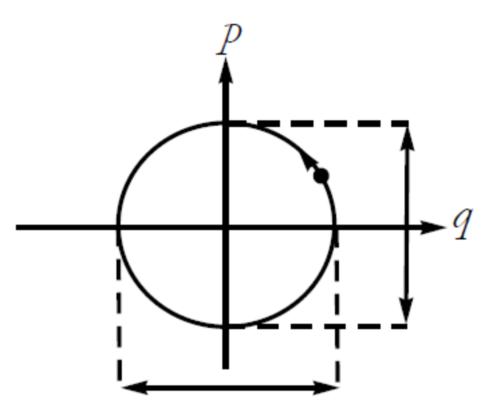
图1. 谐振子的相空间轨迹

一般情况下，系统的相空间轨迹会比谐振子的相空间轨迹更复杂，对称程度也更低。但是相空间的点位于等能线上这一结论是普适的。我们后面会讨论相空间轨迹更一般的性质。

导出哈密顿方程

下面我们给出哈密顿方程的一般性推导。拉格朗日量是坐标和速度的函数：

\[L=L(\{q\},\{\dot{q}\}) \]

哈密顿量为

\[H=\sum_i(p_i\dot{q}_i)-L \]

哈密顿量变分：

\begin{equation*} \begin{split} \delta H & = \sum_i(p_i\delta \dot{q}_i+\dot{q}_i\delta p_i ) - \delta L\\ &=\sum_i\left (p_i\delta \dot{q}_i+\dot{q}_i\delta p_i - \frac{\partial L}{\partial q_i}\delta q_i -\frac{\partial L}{\partial \dot{q}_i}\delta \dot{q}_i \right ) \end{split} \end{equation*}

因为\(p\_i=\frac{\partial L}{\partial \dot{q}\_i}\)，上式中第一项和最后一项正好抵消，于是上式变为：

$$\delta H=\sum_i\left (\dot{q}_i\delta p_i - \frac{\partial L}{\partial q_i}\delta q_i \right )$$

根据变分规则，

$$\delta H\left (\{q\},\{p\}\right )=\sum_i\left ( \frac{\partial H}{\partial p_i}\delta p_i+ \frac{\partial H}{\partial q_i}\delta q_i \right )$$

上面两式对比，可得：

\begin{equation} \begin{split} & \frac{\partial H}{\partial p_i}= \dot{q}_i\\ & \frac{\partial H}{\partial q_i}= -\frac{\partial L}{\partial q_i} \end{split} \label{eq18} \end{equation}

还差最后一步，欧拉-拉格朗日方程写成如下形式：

\[\frac{\partial L}{\partial q_i }=\dot{p}_i \]

带入方程\eqref{eq18}，就得到一般形式的哈密顿方程：

\begin{equation} \begin{split} & \frac{\partial H}{\partial p_i}= \dot{q}_i\\ & \frac{\partial H}{\partial q_i}= -\dot{p}_i \end{split} \label{eq19} \end{equation}