《浅谈亚 log 数据结构在 OI 中的应用》阅读随笔
这篇又长长长了!
早就馋这篇了!终于学了(
压位 Trie 确实很好写啊 但是总感觉使用范围不是很广的样子
似乎是见的题少
原文里都在用 ,但我不是很习惯,所以还是用 。
不出意外的话下一篇是 EI 树。出了意外的话(指完全看不懂)就咕咕咕。
引言
数据结构!该学还是得学的,这给你讲讲亚 的,挺nb!但是有些没用的就不说了,常数大还难写。这讲讲压位 Trie 和 vEB 树。
这玩意用来解决动态前趋问题(Dynamic Predecessor Problem)。我还给你测了测,反正你知道这玩意厉害就行了!这里是代码!
反正不要钱,多少看一点~
1
你需要写一种数据结构,维护一个数字集合。需要支持以下几种操作:
- 若原来不存在数 ,插入数 ;
- 若原来存在数 ,删除数 ;
- 求数 的前趋(前趋定义为小于 且最大的数,若不存在输出 );
- 求数 的后继(后继定义为大于 且最小的数,若不存在输出 );
假设操作数为 ,保证 。
时间限制:
空间限制:
常见解法
- 平衡树
不展开。卡时间还卡空间,它已经死力 - 树状数组
可以树状数组维护 01,树状数组上二分解决。
单次时间复杂度是 ,空间复杂度是 。常数小但是太慢了。 - 整型压位
适用于值域在 以内的情况。
可以使用 等函数和位运算在 复杂度内解决。
2 压位 Trie
压位 Trie,又称 叉 Trie,常数小还好写。
各操作的复杂度均为 ,并且具有较高的拓展性。这里的 常取 ,使用 unsigned long long 压位。
2.1 结构
假设 。
一棵大小为 的压位 Trie 可以维护一个值域为 的集合。
如果 ,显然可以使用一个整型压位解决。下面只讨论 的情况。
我们定义 ,。两个函数的作用是取 的低 位与高位。
对于一棵大小为 的压位 Trie,其有 棵大小为 的子压位 Trie ,其中 维护目前高位为 的值的低位组成的集合。每个节点维护一个 大小的 word 维护第 棵子树内是否维护了值。
论文里的图:
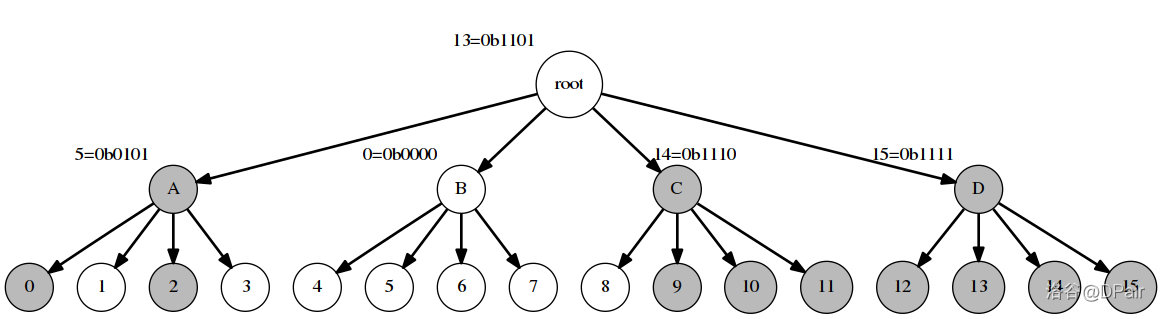
当 的情况。这棵压位 Trie 维护了 里的值,集合为 。可以看到每一个节点的 word。
2.2 插入/删除
假设现在在一棵大小为 的压位 Trie 中插入元素 。首先需要将 插入 中。然后递归。结束了!
删除同理。递推地删除掉只有 的子树对其父亲的标记即可。如果子树删后非空退出即可。
每次都会进入一个大小为原来的 的压位 Trie 中,因此插/删的复杂度为 的。
2.3 前趋/后继
假设现在在一棵大小为 的压位 Trie 中查询元素 的前趋。我们首先在 里查询 的前趋。查到了就退出。
到这了就是没查到。找一个 满足 而且里面有元素。如果存在就返回这个玩意里面的最大值,不存在返回 。
因为压位 Trie 是对称的,后继平凡。
复杂度还是 的。
2.4 复杂度
发现所有操作都是 的。一般取 ,所以有复杂度 。
假设一棵大小为 的压位 Trie 的空间复杂度为 。容易发现 ,且 。因此 。调整第一层子压位 Trie 个数能做到 的空间复杂度。评价:奥妙重重。
2.5 具体实现
边看代码边说(
you wanna see code? click here!
template<const long long Nb>
struct comp_trie {
#define clz(x) __builtin_clzll(x)
#define ctz(x) __builtin_ctzll(x)
int siz;
vector<vector<ull> > t;
ull a[1 << 6], b[1 << 6];
comp_trie() {
ll nowlen = 1;
while (nowlen <= Nb) {
t.emplace_back(vector<ull>(nowlen));
nowlen <<= 6;
} reverse(t.begin(), t.end());
siz = t.size(); cerr << siz << '\n';
a[0] = 0, b[0] = ~1ull;
for (int i = 1; i < 64; ++ i)
a[i] = a[i - 1] << 1 | 1, b[i] = b[i - 1] << 1;
}
inline void insert(int x) { for (int i = 0; i < siz; ++ i, x >>= 6) t[i][x >> 6] |= 1ull << (x & 63); }
inline void erase(int x) { for (int i = 0; i < siz; ++ i, x >>= 6) if (t[i][x >> 6] &= ~(1ull << (x & 63))) return; }
inline void assign(int x, int i) { i ? insert(x) : erase(x); }
inline int prev(int x) {
int i, pre; ull tmp;
for (i = 0; ; i ++, x >>= 6) {
if (i == siz) return -1;
tmp = t[i][x >> 6] & a[x & 63];
if (tmp) {
pre = (63 ^ clz(tmp)) | (x & ~63);
break;
}
} for (; i; -- i) pre = pre << 6 | (63 ^ clz(t[i - 1][pre]));
return pre;
}
inline int next(int x) {
int i, nxt; ull tmp;
for (i = 0; ; i ++, x >>= 6) {
if (i == siz) return -1;
tmp = t[i][x >> 6] & b[x & 63];
if (tmp) {
nxt = ctz(tmp) | (x & ~63);
break;
}
} for (; i; -- i) nxt = nxt << 6 | ctz(t[i - 1][nxt]);
return nxt;
}
}; comp_trie<100005> Tr;
一个节点就是一个 word。为了空间可以写成五个数组+指针数组的形式,速度应该不是很差。
然后我们就可以从底向上更新了,常数会更小一点(确信
论文里说的关于删除和查询的剪枝都用了,就是,接下来再做操作没意义了就退出。但是这点我不会在插入上实现。想实现但是挂了www
经过少许卡常后是 infoj 的最优解。
2.6 拓展
改个操作。现在是 了,我们需要支持插入删除和查询排名。
新的查询在原来的压位 Trie 结构上无法实现,因为我们无法快速查询前 个子树内总共有几个元素。然后改一下叉数。设现在叉数为 ,每当一个节点的子树插入了 个元素后我们重构一次,计算出每个位置的子树内有多少元素,求前缀和后备用。现在只需要维护最近的 个元素中有几个大于 的,即一个前缀内的子树元素个数,
我们考虑用一个 word 存储目前子树内信息。具体地,我们的 word 里有恰好 个 ,第 个 和第 个 之间的 的个数表示第 棵子树内有几个元素了。最前和最后的 可以去掉。如果向查询前 棵子树有多少元素,就可以查询第 个 的位置,这自然能导出在它前面有几个 。我们可以使用 Method of Four Russians 来优化,即打出一张表,存储每一个不同的查询的答案。插入一个 可以使用位运算平凡解决。如果我们取 ,那么预处理复杂度将小于 ,因此我们能以均摊 的时间复杂度解决这个问题,我们也有一些手段将其变为严格 。
3 vEB 树
压位 Trie 的复杂度里 是在分母上的。所以叉数越大效率越高。但是如果你对 word 的操作复杂度不是 ,那就得不偿失了。
vEB 树(van-Emde Boas Tree)采用了一定的策略,使得其在叉数增加的情况下保证了时间复杂度,因此可以在 的复杂度下支持每个操作。
3.1 结构
一棵大小为 的 vEB 树可以维护一个值域为 的集合。
如果 ,显然可以使用 个布尔值维护。否则我们令 。我们维护 个 大小的子 vEB 树 。
我们定义 ,。
对于一棵 vEB 树维护的集合,我们记录其 和 (若集合为空则分别为 和 )并将除了最小值的元素插入其子 vEB 树中。对于 ,我们在 中插入 。
为加速查找,我们再定义一个大小 的 vEB 树 ,其维护出现的数的高位的集合。 可以加速我们的查询。
3.2 边界
对于一棵空的 vEB 树,我们插入元素 时只需要将 和 都设为 。
对于一棵 vEB 树,其集合大小为 当且仅当其的 。
对于一棵集合大小为 的 vEB 树,我们删除元素时只需要将 和 初始化。
对于一棵大小为 的 vEB 树,假设子 vEB 树 中存在元素 ,就说明本树中存在值为 的元素。
这些操作都可以 完成。
3.3 插入
假设我们要在一棵大小为 的 vEB 树中插入一个元素 。
如果该树为空则直接按边界插入即可。
如果 ,交换 和 后接着插入原来的 。如果 ,更新 。
首先我们需要在 中插入 ,并在 中插入 。容易发现,当 非空时, 中一定已存在 ,所以我们只需要在 中插入。否则 为空,按边界插入即可。因此每次只会向一侧插入元素。
假设 为在大小为 的 vEB 树中插入元素的时间复杂度,我们有 。主定理得 ,而 ,因此总时间复杂度为 。
3.4 删除
假设我们要在一棵大小为 的 vEB 树中插入一个元素 。
如果该树为空则直接按边界删除即可。
如果 ,则我们需要在删除 后求得新的 。新 的高位必定是最小的,所以我们在 中找出高位最小值,并在高位对应的子 vEB 树中找到低位最小值,即可得到新的 。
然后我们需要在 中删除 。删空了就在 中删除 。
如果 维护的集合大小为 ,则在 中删除元素的复杂度为 的,因此这里只会向 递归。反之我们不需要维护 。因此每次只会向一侧删除元素。
复杂度同样是 。
3.5 前趋/后继
假设我们要在一棵大小为 的 vEB 树中查询元素 的前趋。
的前趋与 高位相同当且仅当 的 小于 ,因此可以 判断其前趋是否在 中。如果在的话直接查询 的前趋。
否则, 的前趋一定是 的前趋,这个可以向 递归求得。递归回后取 前趋对应子树的最大值即可。
后继镜像,不展开。总时间复杂度 。
对于前趋,如果 中的最小值大于等于 ,则前趋将是整棵 vEB 树的最小值。
对于后继,发现我们要取子树的最小值。需要注意的是,最小值不在 vEB 树的子结构中。
3.6 注意点
可以将维护集合大小为 的情况特殊判断,采用一个 unsigned long long 型的 word 维护。若 ,即便是维护一个大小为 的集合也只用递归两层,大大减小了常数。
这里注意$老师的模板中 vEB 树的 size 是
由于 vEB 树的结构复杂,因此可以采用 template 语法定义不同大小的 vEB 树,特化小型的 vEB 树也比较方便。
3.7 复杂度
可以发现单次操作的时间复杂度均为 。
对于空间复杂度,假设一棵大小为 的 vEB 树空间复杂度为 。容易得到 。同时有 。
我们可以证明 可能会达到 ,但可以通过调整 vEB 树的叉数得到 的空间复杂度。
在值域大的情况下可以考虑哈希表等方式降低 vEB 树的空间复杂度。
4 对于部分数据结构效率的一些测试
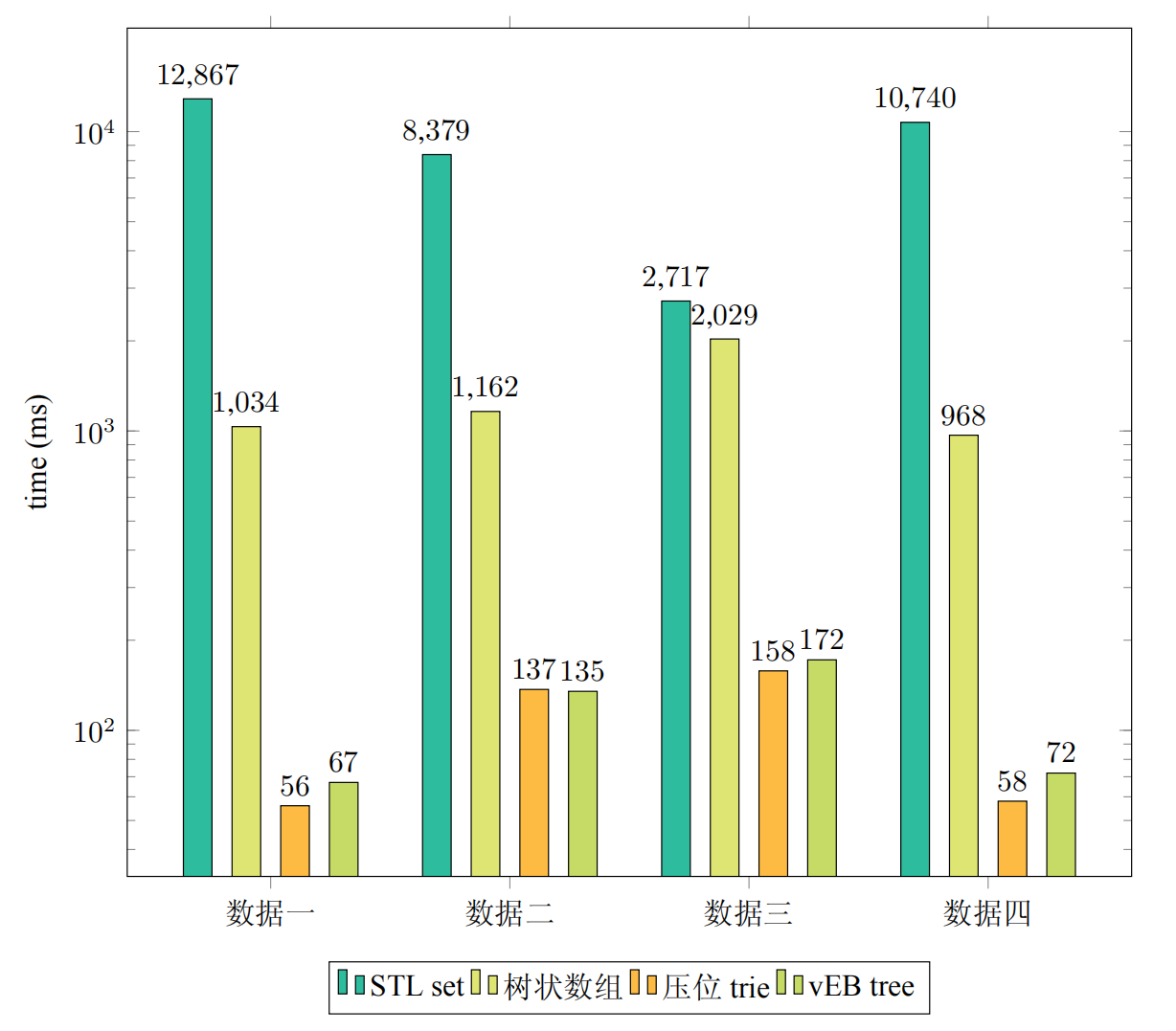
操作次数为 ,值域范围为 。
第一组数据是插入 个不同的数字。
第二组数据是插入 个不同的数字后进行 次前趋/后继查询。
第三组数据是插入 个不同的数字后进行 次前趋/后继查询。
第四组数据是插入 个不同的数字后随机地删除这 个数字。
从时间角度来说:可以发现 vEB 树和压位 Trie 在时间上还是远远快于其它两个 数据结构,在集合数字比较稀疏的情况下的查询甚至比树状数组快了 倍多。相对来说,vEB 树的插入删除略慢于压位 Trie,但是其查询效率还是可以的。这仅仅是随机数据,在更加强力的数据下 vEB 树可能会有相对更高的查询效率。但是压位 Trie 已经完全能够满足我们的使用需求。
从空间角度来说:四个数据结构使用的空间分别为:455MB, 64MB, 2.06MB, 2.03MB。可以见压位 Trie 与 vEB 树在操作数和值域基本同阶的情况下,空间也是非常占优势的。而树状数组的空间也相对来说较小。
从实现难度来说:笔者认为压位 Trie,vEB 树实现难度均在可接受范围之内,而压位 Trie 相对来说更加容易实现,且在很多情况下效率更高。
这段粘的。
5 例题
5.1 [北大集训 2018] ZYB 的游览计划
给定一棵 个节点的树,和一个 的排列 。定义一个整数区间 的权值为从 号节点出发遍历完 (无需按顺序)后回到 号节点需要经过的最小边数。
现在将 划分成 个区间,问权值和的最大值。。
时间限制:。
空间限制:。
可以决策单调性,这里不提。
容易发现我们沿着 dfs 序从小到大遍历一定是最优的。因此我们需要维护一个有序集合中任意两个点的距离以及 号节点和 dfs 序最小/最大的点的距离。
插入一个点 :求出点的前趋 和后继 ,答案变化 。
删除一个点 :求出点的前趋 和后继 ,答案变化 。
使用 vEB 树或压位 Trie 实现可以做到 。
使用压位 Trie 的实现经测试可以做到 150ms 左右。
5.2 [ZJOI2019] 语言
有一棵 个顶点的树,和 条树上的链 。对于一条链,链上的任意不同的两个点之间都可以展开贸易活动。
询问一共有多少点对之间可以开展贸易活动。
时间限制:
空间限制:
动态开点压位 Trie 合并?
先叨叨原题做法。维护一些点的虚树大小,支持虚树合并。可以直接线段树合并。
然后现在有一个压位 Trie,拉过来考虑。
因为是动态开点压位 Trie,所以每个点需要维护所有子节点的编号。每次合并需要把一棵树的子节点编号扔到另一棵树上。根据线段树合并的启发式做法,这玩意的复杂度是 的。
但是空间复杂度有点问题,同一时刻最多是 个节点,不太行。
考虑一个树启。我们直接拿原重儿子的压位 Trie 过来,任意时刻只有 个压位 Trie,每个 Trie 只有 个点,总空间复杂度为 。

以下是博客签名,与正文无关。
请按如下方式引用此页:
本文作者 joke3579,原文链接:https://www.cnblogs.com/joke3579/p/paperessay221130.html。
遵循 CC BY-NC-SA 4.0 协议。
请读者尽量不要在评论区发布与博客内文完全无关的评论,视情况可能删除。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】