闲话 22.12.13
闲话
今天比较想摆
计数 \(n\) 个点的有标号无向图,满足每个点的度数是 \(2\)。
咋写啊?
有社论推荐吗?
看不懂计数题解咋办?
续写续写
大概都知道我要写啥了吧?放个插件
植物大战僵尸
当时讲的时候觉得没啥应用 转头打脸了
就是求最大权闭合子图。我们把关系抽象成图,”吃掉 A 才能吃 B“就连一条 \(B\to A\) 的边,表示选了 \(B\) 必须要选 \(A\)。然后我们需要从这个图里选出一个闭合的子图(没有向子图外连的边)。
咋求呢?我们首先建出原图,边权全是正无穷,再整两个超级点。源点连所有权为整数的值,边权为权,汇点连所有权为负数的值,边权为负权。然后最大权就是正权加和减去最小割。
咋证的不会。我们仍然沿用 happiness 模型,这里割了连源的边就是不选,割了连汇的边就是选。然后你肯定不能割原图的边,则有一条 \(S\to u \to v\to T\) 的路径的话肯定要选 \(v\) 或不选 \(u\)。正确性显然了。
注意先做一遍拓扑排序,删掉成环的植物和它们指向的植物。
code
const int N = 2e6 + 5;
const int inf = 0x3f3f3f3f;
const ll infll = 0x3f3f3f3f3f3f3f3fll;
int M, s, t, n, m, t1, t2, ans, sc[1005], at[1005], deg[1005];
vi g[1005]; bool vis[1005];
#define id(i, j) ( ((i) - 1) * m + (j) )
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> m;
M = n * m; s = ++ M, t = ++ M;
rep(i,1,n) rep(j,1,m) {
if(j < m) {
g[id(i, j + 1)].eb(id(i, j));
// adde(id(i, j), id(i, j + 1), inf);
deg[id(i, j)] ++;
}
cin >> sc[id(i, j)] >> at[id(i, j)];
rep(k,1,at[id(i, j)]) {
cin >> t1 >> t2; ++ t1, ++ t2;
g[id(i, j)].eb(id(t1, t2));
// adde(id(t1, t2), id(i, j), inf);
deg[id(t1, t2)] ++;
}
}
queue<int> que;
rep(i,1,n) rep(j,1,m) if (deg[id(i, j)] == 0) que.emplace(id(i, j)), vis[id(i, j)] = 1;
while (que.size()) {
int u = que.front(); que.pop();
for (auto v : g[u]) {
-- deg[v];
if (!vis[v] and deg[v] == 0) vis[v] = 1, que.emplace(v);
}
}
rep(i,1,n) rep(j,1,m) if (vis[id(i, j)]) {
if (sc[id(i, j)] > 0) adde(s, id(i, j), sc[id(i, j)]), ans += sc[id(i, j)];
else adde(id(i, j), t, - sc[id(i, j)]);
for (auto v : g[id(i, j)]) if (vis[v]) adde(v, id(i, j), inf);
}
cout << ans - Dinic(s, t) << '\n';
}
清理雪道
最小……流?
没错,有源汇上下界最小流。
咋成图呢?假设你原来要连一条 \((u,v), [l,r]\) 的边,那就连一条 \((u, v, r - l)\) 的边,然后开一个数组 \(d\),\(d_u\) 减去 \(l\),\(d_v\) 加上 \(l\)。成原图后在原图的源汇外建超级源汇,如果 \(d_i > 0\) 就和源连,反之和汇连,容量就是 \(|d_i|\)。然后以超级源汇为源汇跑一遍最大流。再加一条原图汇到源的 \([0,\inf]\) 边,在残量网络上跑超级源汇的最大流,这条边的流量就是最小流。
好奇妙啊!感性理解即可吧!发现这个就是在可行流的基础上在加转移边前跑了一遍最大流,这样能将转移的流/不满足流量守恒的流量尽可能减少,也就是尽可能减少了源到汇的浮动流量。浮动流量的最小值不就是最大流吗?
code
const int N = 2e6 + 5;
const int inf = 0x3f3f3f3f;
const ll infll = 0x3f3f3f3f3f3f3f3fll;
int M, s, t, S, T, n, m, ans, t1, t2, t3, t4;
int head[2][N], mlc = 1;
struct ep {
int to, next, flow;
} e[N << 1];
void __Adde(int u, int v, int f) {
e[++ mlc] = { v, head[0][u], f };
head[0][u] = mlc;
e[++ mlc] = { u, head[0][v], 0 };
head[0][v] = mlc;
}
int d[N];
void adde(int u, int v, int Min, int Max) {
__Adde(u, v, Max - Min);
d[u] -= Min, d[v] += Min;
}
int dep[N];
bool bfs(int s, int t) {
rep(i,1,M) dep[i] = 0, head[1][i] = head[0][i];
queue<int> que;
que.push(s); dep[s] = 1;
while (que.size()) {
int u = que.front(); que.pop();
for (int i = head[0][u], v; i; i = e[i].next) {
v = e[i].to;
if (e[i].flow and !dep[v]) {
dep[v] = dep[u] + 1;
if (v == t) return 1;
que.push(v);
}
}
} return dep[t];
}
int dfs(int u, int in, int t) {
if (u == t) return in;
int out = 0;
for (int &i = head[1][u], v; i; i = e[i].next) {
v = e[i].to;
if (e[i].flow and dep[v] == dep[u] + 1) {
int res = dfs(v, min(in, e[i].flow), t);
if (res == 0) dep[v] = 0;
in -= res, out += res;
e[i].flow -= res, e[i ^ 1].flow += res;
if (in == 0) break;
}
} return out;
}
int Dinic(int _s, int _t) {
rep(i,1,M) {
if (i == S or i == T) continue;
if (d[i] > 0) __Adde(S, i, d[i]);
else if (d[i] < 0) __Adde(i, T, -d[i]);
}
while(bfs(_s, _t)) dfs(_s, inf, _t);
adde(t, s, 0, inf);
while(bfs(_s, _t)) dfs(_s, inf, _t);
return e[mlc].flow;
}
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n;
M = n, s = ++ M, t = ++ M, S = ++ M, T = ++ M;
rep(i,1,n) {
adde(s, i, 0, inf), adde(i, t, 0, inf);
cin >> t1;
while (t1 --) {
cin >> t2;
adde(i, t2, 1, inf);
}
}
cout << Dinic(S, T);
}
老C的方块
除了思考难度和代码难度外没有难度的题
就是你看啊 这结构的成型是不是有点刻意?我们是不是能把每个结构都串起来?
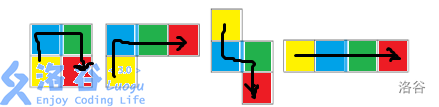
会了吧?我们得保证没有上面那样的情况出现,也就是说求解最小割。然后这就变成了染色后分成好几层,每层间串起来求最小割的题了。怎么染色呢?看第 \(3,4\) 两个图形你大概就能构造出方法了。如下:
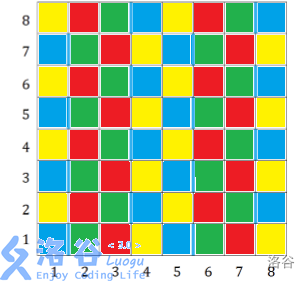
染色求解就行了。具体看代码吧,没什么注意的点。
注:图来自 Danno 的题解。
code
#include <bits/stdc++.h>
using namespace std; using pii = pair<int,int>; using vi = vector<int>; using vp = vector<pii>; using ll = long long;
using ull = unsigned long long; using db = double; using ld = long double; using lll = __int128_t;
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
template <typename T> T rand(T l, T r) { return uniform_int_distribution<T>(l, r)(rnd); }
template <typename T1, typename T2> T1 min(T1 a, T2 b) { return a < b ? a : b; }
template <typename T1, typename T2> T1 max(T1 a, T2 b) { return a > b ? a : b; }
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define ufile(x)
#define rep(i,s,t) for (register int i = (s), i##_ = (t) + 1; i < i##_; ++ i)
#define pre(i,s,t) for (register int i = (s), i##_ = (t) - 1; i > i##_; -- i)
#define Aster(i, s) for (int i = head[s], v; i; i = e[i].next)
#define all(s) s.begin(), s.end()
#define eb emplace_back
#define pb pop_back
#define em emplace
const int N = 1e6 + 5;
const int inf = 0x3f3f3f3f;
const ll infll = 0x3f3f3f3f3f3f3f3fll;
int M, s, t, n, m, k, t1, t2, t3, t4;
int dx[] = { 0, 0, -1, 1 }, dy[] = { -1, 1, 0, 0 };
vp stk;
unordered_map <long long, pii> mp;
#define id(i, j) ( 1ll * ((i) - 1) * m + (j) )
int col(int x, int y) {
// yellow -> blue -> green -> red
// src -> yellow cost= yellow
// yellow -> blue INF
// blue -> green cost= min(blue, green)
// green -> red INF
// red -> dst cost= red
if (x % 4 == 1) {
if (y & 1) return 3; // blue
else return 4; // yellow
} else if (x % 4 == 2) {
if (y & 1) return 1; // green
else return 2; // red
} else if (x % 4 == 3) {
if (y & 1) return 2;
else return 1;
} else {
if (y & 1) return 4;
else return 3;
}
}
int head[2][N], mlc = 1;
struct ep {
int to, next, flow;
} e[N << 1];
void adde(int u, int v, int f, bool __same = false) {
// cout << u << " -> " << v << ' ' << f << endl;
e[++ mlc] = { v, head[0][u], f };
head[0][u] = mlc;
e[++ mlc] = { u, head[0][v], __same ? f : 0 };
head[0][v] = mlc;
}
int dep[N];
bool bfs(int s, int t) {
rep(i,1,M) dep[i] = 0, head[1][i] = head[0][i];
queue<int> que;
que.push(s); dep[s] = 1;
while (que.size()) {
int u = que.front(); que.pop();
for (int i = head[0][u], v; i; i = e[i].next) {
v = e[i].to;
if (e[i].flow and !dep[v]) {
dep[v] = dep[u] + 1;
if (v == t) return 1;
que.push(v);
}
}
} return dep[t];
}
int dfs(int u, int in, int t) {
if (u == t or in <= 0) return in;
int out = 0;
for (int &i = head[1][u], v; i; i = e[i].next) {
v = e[i].to;
if (e[i].flow and dep[v] == dep[u] + 1) {
int res = dfs(v, min(in, e[i].flow), t);
in -= res, out += res;
e[i].flow -= res, e[i ^ 1].flow += res;
if (in <= 0) break;
}
}
if (out <= 0) dep[u] = 0;
return out;
}
int Dinic(int s, int t) {
int ret = 0, fl;
while (bfs(s, t)) while (fl = dfs(s, inf, t)) ret += fl;
return ret;
}
signed main() {
cin >> n >> m >> k;
s = ++ M, t = ++ M;
rep(i,1,k) {
cin >> t1 >> t2 >> t3;
stk.eb(t1, t2);
mp[id(t1, t2)] = {++ M, t3};
t4 = col(t1, t2);
if (t4 == 2) adde(M, t, t3);
if (t4 == 4) adde(s, M, t3);
}
for (auto [x, y] : stk) rep(i,0,3) {
int vx = x + dx[i], vy = y + dy[i];
if (vx < 1 or n < vx or vy < 1 or m < vy) continue;
t1 = col(x, y), t2 = col(vx, vy);
if (t1 == 1) {
if (t2 == 2) {
adde(mp[id(x, y)].first, mp[id(vx, vy)].first, inf);
} else if (t2 == 3) {
continue;
}
} else if (t1 == 2) {
if (t2 == 1) {
continue;
} else if (t2 == 4) {
continue;
}
} else if (t1 == 3) {
if (t2 == 1) {
adde(mp[id(x, y)].first, mp[id(vx, vy)].first, min(mp[id(x, y)].second, mp[id(vx, vy)].second));
} else if (t2 == 4) {
continue;
}
} else {
if (t2 == 2) {
continue;
} else if (t2 == 3) {
adde(mp[id(x, y)].first, mp[id(vx, vy)].first, inf);
}
}
}
cout << Dinic(s, t) << '\n';
}
餐巾计划问题
本人!已经拿起那块最初的餐巾了!
就是用一单位的流来模拟一块餐巾。每天拆成两个点,一个点收干净餐巾一个点发放脏餐巾。这两个点间的流量是 \([r_i, \inf]\)。然后整个源点表示买餐巾,费用是 \(p\),流量是 \([0, \inf]\)。保存就往下一天的脏餐巾连,流量 \([0, \inf]\)。快洗和慢洗就直接连对应天的干净餐巾,费用是 \(f_i/s_i\)。
跑就行了。其实我写这题是这几天一看到这题就想到大总统(
code
int M, s, t, n, m, t1, t2, t3, t4;
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n;
M = n << 1, s = ++ M, t = ++ M;
rep(i,1,n) cin >> t1, adde(s, i + n, t1, 0), adde(i, t, t1, 0);
cin >> t1 >> m >> t2 >> t3 >> t4;
rep(i,1,n-1) adde(i + n, i + 1 + n, inf, 0);
rep(i,1,n - m) adde(i + n, i + m, inf, t2);
rep(i,1,n - t3) adde(i + n, i + t3, inf, t4);
rep(i,1,n) adde(s, i, inf, t1);
Dinic(s, t);
cout << min_cost << '\n';
}
以下是博客签名,与正文无关。
请按如下方式引用此页:
本文作者 joke3579,原文链接:https://www.cnblogs.com/joke3579/p/chitchat221213.html。
遵循 CC BY-NC-SA 4.0 协议。
请读者尽量不要在评论区发布与博客内文完全无关的评论,视情况可能删除。


