分拆、杨图和杨表
目录
\(1.\) 定义和性质
\(\textbf{定义 1 } \text{(分拆)}\)
定义整数 \(n\) 的一个分拆为 \(\lambda = (\lambda_1, \lambda_2, \dots, \lambda_m)\)，满足 \(\forall i, \lambda_i \ge \lambda_{i + 1}\)，且 \(n = \lambda_1 + \cdots + \lambda_m\)。记其为 \(\lambda \vdash n\)，并令 \(\lvert \lambda \rvert = n\)，\(\ell (\lambda) = m\)。
对分拆和有基础限制分拆的计数不再展开，可以由生成函数直接推导得到结果。
杨表的组合结构可能来自于这样一个有趣的问题：有一个直角形状、大小无限的桶，现在要向其中放入 \(n\) 个大小相同的球，形成一个稳定的形状。那么，有多少种放球的方案呢？
一种依次放入五个球的例子如下：
我们该如何将这样的方案抽象成组合结构呢？分拆为我们提供了一种方法——
\(\textbf{定义 2 } \text{(杨图)}\)
对一个分拆 \(\lambda \vdash n\)，形状为 \(\lambda\) 的杨图（Young diagram）为一个 \(\ell (\lambda)\) 行、第 \(i\) 行由 \(\lambda_i\) 个单位方格排列而成的表格，每行的方格左对齐，记作 \([\lambda]\)。称 \([\lambda]\) 的高度为 \(\ell(\lambda)\)。
若将单位方格换为单位点，其便被称为 Ferrers 图。
有三种画杨图的方式：英式，短行在下；法式，长行在下；俄式，直角在下。一般采用英式画法（虽然 tableaux 是法文）。
若对 \(\lambda \vdash n\) 和 \(\mu \vdash n\)，有 \(\ell (\lambda) \ge \ell (\mu)\)，且 \(\forall i, \lambda_i \ge \mu_i\)，那么我们称 \(\lambda\) 包含 \(\mu\)，记作 \(\mu\subset\lambda\)。容易看出这包含关系是分拆集合上的一个偏序关系。
杨图中每个单位方格的位置可以唯一地用其所在行和列表示。若我们将行按照方格数由大到小、列按照由左向右标号（由 \(1\) 开始），那么一个杨图 \([\lambda]\) 可以被表示为集合 \(\{(i, j)\mid 1\le i\le \ell(\lambda), 1\le j\le \lambda_i\}\)。这样若 \(\lambda\) 包含 \(\mu\)，有 \([\mu] \subseteq [\lambda]\)。
对这种集合表示方法，我们也可以推广一下，用 \(\mathbb Z^2\) 的子集来表示一个图（diagram）。这里的横坐标表示行数，其由上到下递增；纵坐标表示列数，其由左到右递增。按四联通的方式建图，我们也可以自然地定义图论相关性质。
一个分拆 \(\lambda \vdash n\) 也可以被描述为无穷序列 \((\lambda_1, \lambda_2, \dots)\)，只需要令 \(\forall i > \ell (\lambda), \lambda_i = 0\)。定义 \(\lambda\) 的共轭（或转置）分拆为 \(\lambda^{\mathsf T} \text{ s.t. } \forall \lambda^{\mathsf T}_k = \left\lvert \left\{ i > 0 \mid \lambda_i \ge k\right\} \right\rvert\)。若把这过程放在图形上，那么 \([\lambda]\) 到 \([\lambda^{\mathsf T}]\) 就是沿主对角线作对称，或行列互换。
\(\textbf{定义 3 } \text{(杨表)}\)
对一个形状为 \(\lambda \vdash n\) 的杨图 \([\lambda]\)，若将 \(1\sim n\) 这 \(n\) 个正整数填入每个单位方格，使得每一行从左到右、每一列从上到下的数字都严格递增，就得到了一个形状为 \(\lambda\) 或 \([\lambda]\) 的（标准，standard）杨表（Young tableaux）。容易知道，正整数集可以被替换为任意具有全序的集合，这时的杨表被称作近似（near）杨表。普通杨表也是近似杨表。
若这 \(n\) 个正整数可以被重复填入，那么就会存在非严格递增的情况。若每一行从左到右的数字非严格递增，但每一列从上到下的数字严格递增，就得到了半标准（semistandard）杨表。
对一个形状为 \(\lambda \vdash n\) 的杨表，其权重为 \((c_1, c_2, \dots, c_n)\)，其中 \(c_i\) 表示 \(i\) 在杨表中出现的次数。容易知道标准杨表的权重必定为 \((1, 1, \dots, 1)\)。
记杨表 \(P\) 的形状为 \(\text{sh}(P)\)，其既可以是分拆，也可以是杨图。
对杨图 \(D\)，令 \(\text{SYT}(D)\) 为形状为 \(D\) 的标准杨表组成的集合，并令 \(f^D = \lvert \text{SYT}(D) \rvert\)。对分拆 \(\lambda\) 类似地定义上述记号。注意到若 \(\lambda\) 的转置为 \(\lambda'\)，则 \(f^\lambda = f^{\lambda'}\)。例如：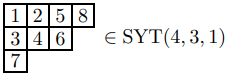
\(\textbf{定义 3 } \text{(斜)}\)
对两个分拆 \(\lambda, \mu\)，若 \([\mu] \subseteq [\lambda]\)，那么形状为 \(\lambda / \mu\) 的斜（skew）杨图 \([\lambda / \mu]\) 由集合差 \([\lambda] / [\mu]\) 定义，即集合 \(\{(i, j) \in [\lambda]\mid \mu_i + 1\le j\le \lambda_i\}\) 对应的图。
斜杨表的定义与杨表类似，对数字的限制相同，只是需要将其填入斜杨图。
例如：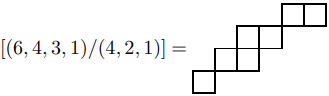
下文中的“杨表”指代标准杨表。
\(2.\) 确定杨图，对杨表的计数
\(\textbf{定理 1 } \text{(钩长公式)}\)
对任意分拆 \(\lambda\)，以及其杨图中的一个方格 \(c = (i, j) \in [\lambda]\)，定义其钩（hook）为
\[H_c = [\lambda] \cap \left(\{(i, j)\} \cup \{(i, j’) \mid j' > j\} \cup \{(i', j) \mid i' > i\} \right) \]即 \(c\) 及其正右方、正下方的格子。其钩长（hook length）为 \(h_c = \lvert H_c \rvert = \lambda_i + \lambda^{\mathsf T}_j - i- j + 1\)。那么有钩长公式（hook length formula）
\[f^\lambda = \frac{\left\lvert \lambda \right\rvert !}{\prod_{c\in [\lambda]} h_c} \]
证明：我们将使用一个概率论的方法\({}^{[4]}\)。
取自然数列 \((\lambda_1, \lambda_2, \dots)\)。若 \(\lambda \vdash n\)，则令 \(F(\lambda_1, \lambda_2, \dots)\) 为定理 \(1\) 中的 RHS，反之令其为 \(0\)。考虑 LHS 的组合意义，我们需要递推，每次加入一个元素。考虑元素 \(n\)。由于 \(n\) 大于当前杨表中任意其他元素，其必定在某行/列的末尾位置（角落，钩长为 \(1\)）。因此不妨令 \(n\) 位于第 \(\alpha\) 行，我们要证明的就是
简记为
注意上式确实枚举了所有的角落，这是由于若 \(\alpha\) 行不出现角落，那么 \(\lambda_{\alpha + 1} = \lambda_\alpha\)，从而 \(\lambda_{\alpha + 1} > \lambda_\alpha - 1\) 使得这样的 \(F_\alpha = 0\)。
我们为什么要这样定义呢？这是由于，通过每次加入 \(n\)，我们可以得到所有的杨表，因此上式所拥有的结构的组合意义符合杨表的组合意义。我们只需要证明上式成立，也就是 RHS 具有和 \(f^\lambda\) 同样的组合形式，这也就证明了原式的等号。整理得到，我们要证明的就是
考察一个基于杨图的随机过程，我们维护一个指针，并进行如下的操作：
- 初始，随机选择一个格子指向它；
- 在这个格子的钩中选一个格子，将指针指向它，随后检查当前位置；
- 若指针指向的格子在角落，结束这一过程；
- 反之，执行 \(2.\) 操作。
设这一过程结束于角落 \((\alpha, \beta)\) 的概率为 \(p(\alpha, \beta)\)。显然有 \(\sum_{\alpha} p(\alpha, \beta) = 1\)。因此，我们只需要证明
令 \(p(A, B\mid a_1, b_1)\) 为该过程起始于 \((a_1, b_1)\)，终结于 \((\alpha, \beta)\)，路径上经过的横坐标组成集合 \(A = \{a_1, a_2, \dots\}\)，纵坐标组成集合 \(B = \{b_1, b_2, \dots\}\) 的概率。考虑第一步是水平方向还是竖直方向，可以得到
使用归纳法，我们要证明
这是由于 \(p(A / \{a_1\}, B \mid a_2, b_1) = (h_{(a_1, \beta)} - 1) \text{RHS}\)，\(p(A, B / \{b_1\}\mid a_1, b_2) = (h_{(\alpha, b_1)} - 1) \text{RHS}\)。但由于 \(h_{(a_1, b_1)} + 1 = h_{(a_1, \beta)} + h_{(\alpha, b_1)}\)，知道
首先随机选择起始点 \((a, b)\)，并令 \(A \subseteq \{1, \dots, \alpha\}, B \subseteq \{1, \dots, \beta\}\) 有 \(a = \min A, b = \min B\)，我们有
化简即可。\(\square\)
例如，\((1, 2)\) 的钩形如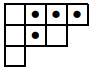
\(\textbf{定理 2 } \text{(F. G. Frobenius, 1900)}\)
对分拆 \(\lambda\)，令 \(l_i = \lambda_i + \ell (\lambda) - i\)，那么
\[f^\lambda = \frac{\lvert \lambda\rvert !}{\prod_{i = 1}^{\ell (\lambda)} l_i !} \prod_{i < j} (l_i - l_j) \]
证明：等价于定理 \(1\)。\(\square\)
\(\textbf{定理 3 } \text{(行列式公式)}\)
令 \(\forall k < 0, (k!)^{-1} = 0\)。对分拆 \(\lambda\)，
\[f^\lambda = \lvert \lambda\rvert ! \det \left\{\dfrac{1}{(\lambda_i - i + j)!}\right\}_{i, j=1}^{\ell(\lambda)} \]
证明：考察下降幂的形式，化简并按照范德蒙德行列式的形式展开，其等价于定理 \(2\)。\(\square\)
\(3.\) RSK 算法
虽然这是一个算法，但它实际上指出了一个排列与杨表对的双射。RSK 分别是 G. de B. Robinson，C. Schensted 和 D. E. Knuth。是你，高德纳！
下面我们将构造一个双射，从而证明
令 \(\pi\) 对应的杨表对为 \((P_\pi, Q_\pi)\)。
RHS 的组合意义是经典的：长度为 \(n\) 的排列的数目，即 \(\lvert\mathcal S_n\rvert\)，但右侧该怎么得到呢？这就是 RSK 算法的核心思路：维护两个杨表，构造依排列顺序插入元素的操作，并通过一些限制使得其形状保持相同。
既然依排列顺序，那么我们就不能保证插入过程中维护的是杨表，而只能保证这是一个近似杨表。假设我们有一个近似杨表 \(P\)，记 \(P\leftarrow k\) 为将 \(k\) 自第一行插入 \(P\) 的操作，称其为一次行插入。需要执行如下的程序：
- 执行过程中，维护当前行变量 \(c\) 与当前值变量 \(k\)，\(c\) 初始化为 \(1\)，\(k\) 初始化为要插入的值。
- 寻找最小的 \(r\) 使得 \(P_{(c, r)} > k\)。
- 若不存在这样的 \(r\)，那么将 \(k\) 插入第 \(c\) 行的末尾定满足要求。插入后结束程序。
- 反之，交换 \(k\) 与 \(P_{(c, r)}\)，并将 \(c\) 自增 \(1\)，判断是否越界。
- 若不存在第 \(c\) 行，则新建一行，将 \(k\) 作为 \(P_{(c, 1)}\)。
- 反之，执行 \(2.\) 操作。
同样，可以定义 \(k \rightarrow P\) 为将 \(k\) 自第一列插入 \(P\) 的操作，称其为一次列插入。
下面就可以描述 RSK 算法的程序了。取排列 \(\pi \in \mathcal S_n\)，我们需要构造一个近似杨表对序列 \((P_0, Q_0), (P_1, Q_1), \dots, (P_n, Q_n)\)，使得 \(P_i, Q_i\) 为两个近似杨表，且均包含 \(i\) 个方格。RSK 算法需要执行如下的程序：
- 初始时，令 \((P_0, Q_0) = (\varnothing, \varnothing)\)。随后执行 \(n\) 轮如下操作。
- 第 \(i\) 轮时：
- \(P_i \leftarrow (P_{i - 1} \leftarrow \pi_i)\)
- 将 \(i\) 插入 \(Q_{i - 1}\) 得到 \(Q_i\)，使得 \(P_i, Q_i\) 形状相同。（注意：此处不是行插入）
- 返回 \((P_n, Q_n)\) 作为所需的杨表对 \((P_\pi, Q_\pi)\)。
由于 \(i\) 插入的位置必定为角落，因此 \(Q_n\) 必定为杨表。
令 \(A_{n} = \{(P, Q) \mid \text{sh}(P) = \text{sh}(Q) = \lambda, \lvert \lambda \rvert = n\}\)。通过这一程序，我们自然能得到 \(\mathcal S_n \to A_n\)。反过来怎么做呢？我们可以把行插入也反过来，得到行删除。
令当前的表对为 \((P,Q)\)，我们要删除 \(Q\) 中的 \(t\)，只需要执行以下操作：
- 执行过程中，维护当前行变量 \(c\) 与当前值变量 \(k\)，\(c\) 初始化为 \(t\) 所在行的上一行，\(k\) 初始化为 \(P\) 中 \(t\) 对应位置。
- 寻找第 \(c\) 行中比 \(k\) 大的最小元素 \(k'\)，交换 \(k\) 与 \(k'\)，并将 \(c\) 自减 \(1\)，判断是否越界。
- 若 \(c = 0\)，返回 \(k\) 作为 \(\pi_t\)。
- 反之，执行 \(2.\) 操作。
将如上的行删除倒序执行（即先删除 \(n\)），我们就得到了其对应的排列。\(\square\)
那么，我们如何计算 \(\sum_{\lambda \vdash n} f^\lambda\) 呢？仍然可以考察 RSK 算法，我们知道这时只需要 \(P = Q\)，并计数对应的 \(\pi\) 即可。
注意到 \(\pi \leftrightarrow (P, Q)\) 那么 \(\pi^{-1} \leftrightarrow (Q, P)\)。这时我们知道 \(\pi = \pi^{-1}\)，也就是 \(\pi^2 = 1\)，对应的 \(\pi\) 即 \(n\) 阶对合，其只有大小为 \(1,2\) 的置换环。
知道了这一性质后，计数就变得简单了。令 \(\mathcal C\) 为大小为 \(1, 2\) 的置换环的有标号类，那么所有对合组成的有标号类即为 \(\text{SET}(\mathcal C)\)。翻译成生成函数就是 \(\exp (x + x^2 /2)\)。你当然可以提取系数，可以知道这指出
未免有点太不好看了吧？
\(4.\) RSK，能不能再给力一点啊？
当然可以。就算不相信我，你也要相信高德纳啊！
半标准杨表对应的置换被称作广义置换，其为广义对称群（\(m\) 阶循环群 \(Z_m\) 和 \(n\) 阶对称群 \(S_n\) 的圈积 \(Z_m \wr S_n\)）的元素。我们也可以按照第一维递增的方式排列对应置换，如
每个广义置换都对应一个广义置换矩阵，其中矩阵 \(i\) 行 \(j\) 列的元素表示 \(i\to j\) 的出现次数。如
容易知道置换对应的广义置换矩阵是方阵，且每行每列只有一个 \(1\)。
\(\textbf{定理 4 } \text{(D. E. Knuth, 1970)}\)
存在一个广义置换和形状相同的半标准杨表对的双射，
\[\omega_A \longleftrightarrow (T_A, U_{A}) \]这双射同时也导出了广义置换矩阵和形状相同的半标准杨表对的双射，
\[A \longleftrightarrow (T_A, U_{A}) \]
同时有 \(A^{\mathsf T} \longleftrightarrow (U_A, T_{A})\)。
\(5.\) 确定斜杨图，对斜杨表的计数。你兴奋了吗？
下面该考察斜杨表的计数了。
虽然我们不太喜欢行列式，但斜杨表计数的行列式形式确实是最早发现的。先列一下定理吧。
\(\textbf{定理 5 } \text{(斜行列式公式)}\)
令 \([\mu] \subseteq [\lambda]\)，并 \(\forall j > \ell(\mu)\) 时 \(\mu_j = 0\)，\(\forall k < 0, (k!)^{-1} = 0\)，我们有
\[f^{\lambda/\mu} = \lvert \lambda/\mu\rvert ! \det \left\{\dfrac{1}{(\lambda_i - \mu_i - i + j)!}\right\}_{i, j=1}^{\ell(\lambda)} \]
证明：繁，略去。见 \([3]\) 中定理 \(5.6\) 的证明。\(\square\)
随后就是 2014 年被 H. Naruse 提出、2018 年被 A. H. Morales, I. Pak 与 G. Panova 使用 q-analog 证明的斜钩长公式了。然而乘积公式始终没有很大的进展，目前较为前沿的结果是 Z. Hamaker 等人对 E. A. DeWitt 提出的“楼梯减去矩形”的乘积公式的优化。
表述斜钩长公式需要引入兴奋（excited）运动和兴奋图。注意：这里还没有填数字，和表无关。
对 \(\lambda / \mu\)，一个兴奋图是一个大小为 \(\lvert \mu \rvert\) 的 \([\lambda]\) 的子集（也就是说，我们在 \([\lambda]\) 的 \(\lvert \lambda \rvert\) 个方框里选择 \(\lvert \mu \rvert\) 个，它们组成的图就可能是一个兴奋图）。这个子集由集合 \([\mu]\) 经过一系列兴奋运动得到。
一次兴奋运动只能选择一个属于兴奋图的方框 \(c = (\alpha, \beta)\)，若 \((\alpha + 1, \beta), (\alpha, \beta + 1), (\alpha + 1, \beta + 1)\) 均不属于兴奋图，那么这次运动将 \(c\) 移动到 \((\alpha + 1, \beta + 1)\)，即 \((\alpha, \beta)\) 不再属于兴奋图，\((\alpha + 1, \beta + 1)\) 被加入兴奋图。
令 \(\mathcal E(\lambda / \mu)\) 为所有能通过 \(\ge 0\) 次兴奋运动构造出的兴奋图组成的集合。
\(\textbf{定理 6 } \text{(斜钩长公式)}\)
令 \(\mu \subset \lambda\)，我们有
\[f^{\lambda/\mu} = \lvert \lambda/\mu\rvert ! \sum_{D\in \mathcal E(\lambda / \mu)} \prod_{c\in [\lambda] \setminus D} \frac{1}{h_c} \]
证明：见上方论文。\(\square\)
注意，这里 \(h_c\) 是对 \(\lambda\) 定义的，我们只是改变了求和对象（由 \(\lambda\) 全体改为 \(\lambda\) 中不在 \(D\) 内位置）而已。
\(6.\) 应用
首先不可不提的是 LIS（最长上升子序列）和 LDS（最长下降子序列）的刻画。
对排列 \(\pi\)，知道 \(P_\pi\) 第一行的长度就是 \(\pi\) 的 LIS 长度。做过 LIS 题的都知道，只看第一行，这过程和 \(O(n\log n)\) 求 LIS 长度的方法本质相同，而这方法得到的不一定是 LIS 本身。
\(\textbf{引理 1 } \text{(C. Schensted, 1961)}\)
对一个近似杨表 \(S\) 与两个元素 \(x, y\)，有
\[(x\rightarrow S) \leftarrow y = x\rightarrow (S \leftarrow y) \]
证明：繁，见 Schensted 原论文 Lemma 6。\(\square\)
根据该引理，对排列 \(\pi\)，若翻转 \(\pi\) 得到 \(\mu\)，那么 \(P_{\mu}\) 即为 \(P_{\pi}\) 翻转行列后的杨表。同时由于 \(\pi\) 的 LDS 就是 \(\mu\) 的 LIS，知道这值就是 \(\ell(\text{sh}(P_\pi))\)。但 \(Q_{\mu}\) 不一定为 \(Q_{\pi}\) 翻转行列后的杨表。
随后不可不提的就是 k-LIS 和 k-LDS 了。
对一个排列 \(\pi\)，定义其 k-LIS 子序列为 LIS 长度 \(\le k\) 的子序列，同理定义 k-LDS。我们猜想：取 \(P_\pi\) 的前 \(k\) 列，其大小和最长的 k-LIS 子序列长度相同。证明考虑按 \(P_\pi\) 由下到上，每行由左到右顺序遍历得到的排列和 \(\pi\) 的 k-LIS 子序列长度相同，故选择前 \(k\) 列是可能的最优情况。
懒得写这个应用了，例题扔在这。这定理被 C. Greene 和 D. J. Kleitman 于 1976 年提出。一个推广的尝试见此处。
References
\([1]\): yfz, 浅谈杨氏矩阵在信息学竞赛中的应用;
\([2]\): OI wiki, 杨氏矩阵;
\([3]\): Ron M. Adin et al., Enumeration of Standard Young Tableaux;
\([4]\): Curtis Greene, Albert Nijenhuis, and Herbert S. Wilf, A Probabilistic Proof of a Formula for the Number of Young Tableaux of a Given Shape.
以下是博客签名，与正文无关。
请按如下方式引用此页：
本文作者 joke3579，原文链接：https://www.cnblogs.com/joke3579/p/-/young-tableaux。
遵循 CC BY-NC-SA 4.0 协议。
请读者尽量不要在评论区发布与博客内文完全无关的评论，视情况可能删除。
