闲话 24.6.13

闲话

感觉写的有点长了，当半个社论发了吧（
没啥想写的闲话啊！

今日推歌：所以我放走了那天的流星 by 不鱼_P feat. 星尘 Minus

Stabilized Interval Free

对两个正整数 \(l,r\)，本文使用 \([l, r]\) 表示 \(\{x\in \mathbb N \mid l\le x \le r\}\)。

对排列 \(\pi = (\pi_1, \pi_2, \dots, \pi_n)\)，本文使用 \(\pi(k)\) 表示 \(\pi_k\)，\(\pi(A)\) 表示 \(\{\pi(a) \mid a\in A\}\)。

小周在和 \(n\) 个小孩召开法。她在地上顺序写下了 \(1\) 到 \(n\) 这 \(n\) 个数，并给每个小孩指定了 \(1\) 到 \(n\) 中的一个数，然后让他们随便站成一排，每个人都站在地上的一个数上，最后让他们移动到地上自己指定的数对应的数上。但小周发现，这些小孩有个毛病：如果移动前站在一个区间 \([l, r]\)（\([l, r] \not = [1, n]\)）上的小孩在移动后都还站在这个区间上，他们就会不高兴。小周困惑于：有多少种让这些小孩站成一排的方案，使得没有小孩会在移动后不高兴？

形式化地：定义一个长为 \(n\) 的排列 \(\pi\) 是好的，当且仅当对任意正整数 \(1\le l \le r \le n\) 且 \([l,r] \neq [1,n]\)，存在 \(l\le i \le r\)，使得 \(l\le \pi(i) \le r\) 不成立。计数长为 \(n\) 的好排列。

\(n \le 10^5\)。

本来想出成题的，被原题自动机 jijidawang 提醒存在类似的题。那我就写成闲话吧！

对一个排列 \(\pi\)，如果存在区间 \([l, r]\subsetneq [1, n]\)，使得 \(\pi([l,r]) = [l,r]\)，那么称这个区间是排列 \(\pi\) 的稳定区间（stabilized interval）。可以知道题目中好排列等价于不存在稳定区间的排列，下面称这样的排列是 sif（stabilized interval free）的。

答案对应的序列是 A075834。我们注意到这个页面提供给了我们一个很好看的式子，下面来证明一下。

定理 (D. Callan, 2003)

令 \(a_n\) 为长为 \(n\) 的 sif 排列数，\(A(x)\) 为其生成函数，则有

\[[x^{n-1}] A^n(x) = n! \]

证明：原命题可表述为，取 \(n\) 个可为空排列的 sif 排列，满足它们的长度相加为 \(n-1\)，并将它们顺序排成一个序列，可以构造出的方案数和长为 \(n\) 的排列数相同。下面用双射证明，我们将由一个排列 \(\pi\) 构造出对应的 sif 排列序列，而这种构造方法恰好对应一个双射。

下面将以 \(\pi = (2, 4, 3, 1, 8, 7, 6, 5, 13, 10, 9, 16, 11, 15, 14, 12)\) 为例，将每一步对应的构造展示出来。图源论文。

第一步：将排列分解。
我们总能将排列的下标划分为一系列不交的区间 \(I_1, I_2, \dots, I_k\)，使得 \(\forall I_i\) 是 \(\pi\) 的一个稳定区间。当 \(k\) 取到最大值时，这些区间被称作 \(\pi\) 的 \(k\) 个分量。若 \(\pi\) 只有一个分量，那么称它是连通的。注意：连通的排列不一定是 sif 的，每个分量可以导出的子排列也不一定是 sif 的。例如：\(\pi = (5, 4,3,2,1)\) 是连通的，但不是 sif 的。
我们将排列按照它的分量分解。具体地，对每个分量 \(I_i = [l_i, r_i]\)，令 \(\sigma_i = \left(\pi(l_i), \pi(l_i + 1), \dots, \pi(r_i)\right)\)。\(k\) 取到最大值的方案数必定是唯一的，由于增加分量必定会使某个原来的分量分成两部分，并且分量之间无关。这指出了这样的分解是双射。
例子的分解为 \(\sigma_1 = (2, 4, 3, 1), \sigma_2 = (8, 7, 6, 5) ,\sigma_3 = (13, 10, 9, 16, 11, 15, 14, 12)\)。

第二步：将 \(n\) 删掉。
令 \(p_0\) 满足 \(\sigma(p_0) = n\)，容易知道 \(p_0\) 与 \(n\) 均位于第 \(k\) 个分量。从 \(\sigma_k\) 中删除 \(n\) 后获得 \(\sigma_k'\)，使得 \(\sigma_k'(p_0) = \sigma_k(n)\)。也就是将 \(p_0 \to n\) 与 \(n \to \sigma_k(n)\) 的两条边合为一条。这时 \(\sigma_k'\) 不一定连通，但由于 \(\sigma_k\) 连通，\(p_0\) 必定位于 \(\sigma_k'\) 的第一个分量中。
例子的分解为 \((2, 4, 3, 1) - (8, 7, 6, 5) - (13, 10, 9, 12, 11, 15, 14)\)。

第三步：找到 sif 子序列。
我们将一个 sif 子序列称作原排列的一个块。对每个 \(\sigma_i\)，将其重标号为排列后找到它的稳定区间，按照它们初始时对应的数字记录为块后，将这些数移除。执行该过程若干次，直至 \(\sigma_i\) 重标号为排列后为 sif 排列。将剩余部分记录为块，并全部移除。假设共产生了 \(m\) 个块。
对每个块，按照块内最大元素由小到大排序，令第 \(1\le i\le m\) 个块中最大元素为 \(M_i\)，大小为 \(S_i\)。此时我们需要记录每个块内元素的相对大小关系。由于每个块都对应一个 sif 排列，我们可以用其重标号后的 sif 排列代表该块。
例如 \((2, 4, 3, 1) - (8, 7, 6, 5) - (13, 10, 9, 12, 11, 15, 14)\) 在第一次移除（不执行重标号）过程中移除了 \((3), (7, 6), (10), (12), (15, 14)\)，剩余 \((2, 4, 1) - (8, 5) - (13, 9, 11)\)。第二次移除过程中移除了 \((2,4,1), (8,5), (13, 9, 11)\)。最终的块（按最大值排序）为

\[(3) - (2,4,1) - (7, 6) - (8, 5) - (10) - (12) - (13,9,11) - (15,14) \]

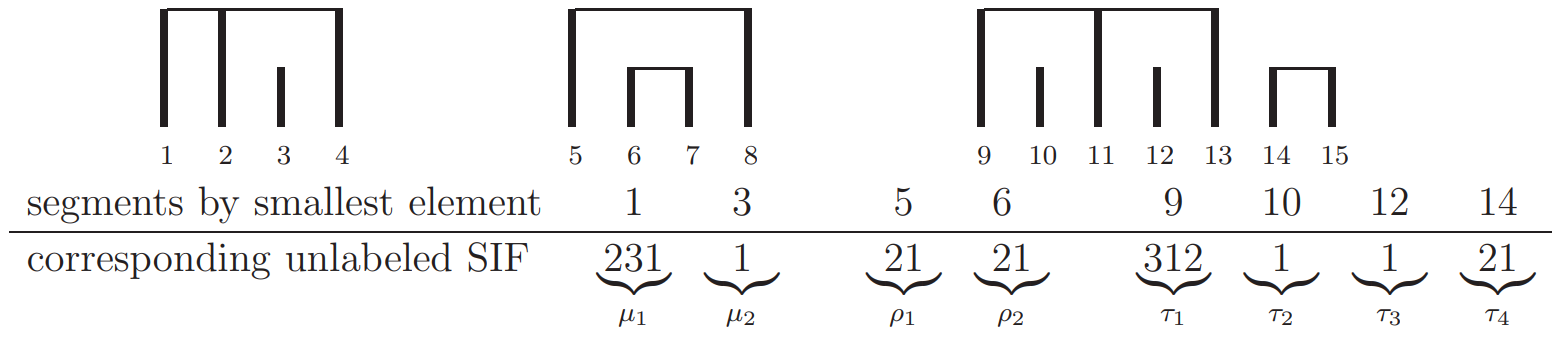
第四步：转成 Dyck 路。
不妨令 \(M_0 = 0\)，则我们可以按照块的信息，构造一个合法的 Dyck 路。具体地，我们从 \((0, 0)\) 出发按照 \(M_1 - M_0\) 个上升、\(S_1\) 个下降、\(M_2 - M_1\) 个上升、\(S_2\) 个下降……\(M_m - M_{m-1}\) 个上升、\(S_m\) 个下降的形式构造，最后会走到 \((2n - 2, 0)\) 的位置，并且不会越过 \(x\) 轴。这是由于一共走了 \(\sum_{i=1}^m (M_i - M_{i - 1}) = M_m - M_0 = M_m = n - 1\) 步上升，\(\sum_{i=1}^m S_i = n - 1\) 个下降，且任意 \(\sum_{i=1}^k (M_i - M_{i - 1}) = M_k \ge \sum_{i=1}^k S_i\)。最后记得标记出来 \(p_0\) 在 \(S_m\) 里对应的上升。
承接上面的，例子构造出的 Dyck 路如下：

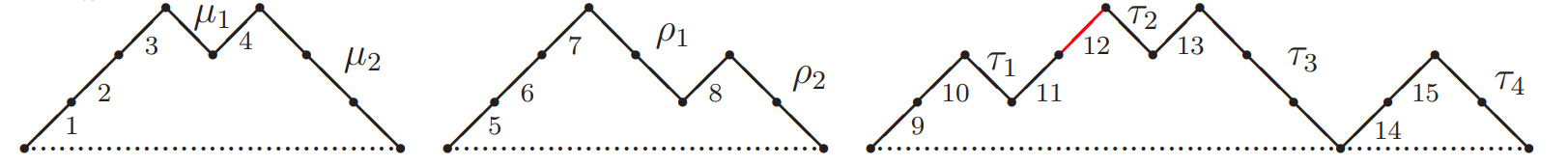
其中 \(M = (3,4,7,8,10,12,13,15)\), \(S = (1,3,2,2,1,1,3,2)\)。

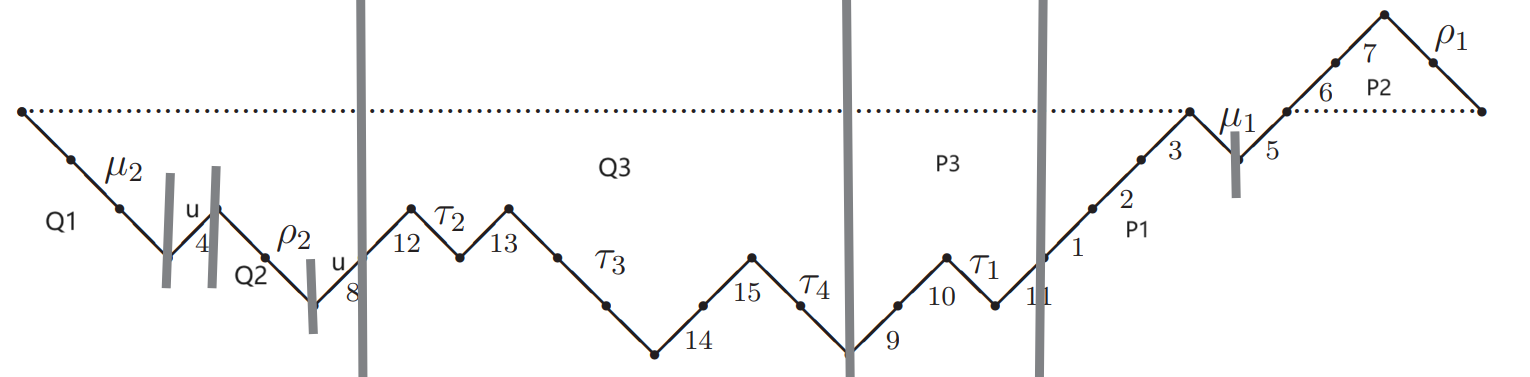
第五步：重新排列 Dyck 路。
对 \(\sigma_k'\) 对应的 Dyck 路，将其分为被标记的上升之前的部分 \(P_k\) 和上升及上升之后的部分 \(Q_k\)。对 \(\sigma_1, \sigma_2, \dots,\sigma_{k-1}\)，将其分为最后一次上升前的段 \(P_i\), 上升\(u\), 和上升后的段 \(Q_i\)。随后按照

\[Q_1, u, Q_2, u, \dots, Q_{k-1}, u, Q_k, P_k, P_1, P_2,\dots, P_{k-1} \]

的顺序重排 Dyck 路，得到一个平衡的格路 \(D\)。
这是一个双射，由于我们可以从重排后的 Dyck 路获得重排前的 Dyck 路。首先，第一个连续两次上升的中点即为 \(Q_k\) 的起点 \(p\)，这是由于 \(Q_k\) 以 \(p_0\) 对应的上升开始，且 \(Q_k\) 前有一个 \(u\)，并且由于 \(Q_i\) 不为空，在这之前的两个 \(u\) 无法连续。并且，\(Q_k\) 的终点是最右侧的最低点 \(l\)，这是由于 \(Q_i, u(i < k)\) 的组合必定不升，\(P_i\) 必定不降（原文说这依赖于被标记的上升位于 \(\sigma_k'\) 的第一个分量）。随后的构造就相对显然了，我们找到 \(l\) 右侧距离其最远的与 \(p\) 等高的点 \(q\)，\(P_k\) 即为 \(l\) 至 \(q\) 的部分。\(p\) 前的下降长度决定了每个 \(Q_i(i < k)\) 的大小，从而决定了 \(q\) 后 \(P_i\) 的长度。因此为双射。
当然需要对一些 corner cases 进行讨论。可能需要在 \(D\) 前后加入上升，来保证连续两次上升的存在，从而确定 \(p\) 点。若 \(D\) 以上升开始，那么 \(p\) 为 \(D\) 的起点，此时 \(k=1\)，原排列连通。若 \(p\) 为 \(D\) 的终点，那么原排列为单位排列，即 \((1, 2, \dots, n)\)。进一步地，若 \(\pi(n) = n\)，则最后一段 Dyck 路为空，就不存在被标记的上升，\(q\) 可能并不存在，此时 \(P_k, Q_k\) 均可为空。
对例子，重排后即为（标记很粗糙，凑合看）

第六步：获得 sif 序列。
将 D 按照 \(n - 1\) 个上升分割为 \(n\) 段，所有段都拥有 \(\ge 0\) 个下降，这些下降对应着一个块，从而对应着一个长为下降数的 sif 排列。除第 \(n\) 段外每段的结尾都为上升。由于一共有 \(n - 1\) 个下降，这些 sif 排列的长度相加为 \(n-1\)。
记空 sif 排列为 \(\emptyset\)，则例子对应的 sif 排列序列为

\[\{(2,3,1), (2,1), \emptyset, (1), (1), \emptyset, (2,1), \emptyset, (3,1,2), \emptyset,\emptyset,\emptyset, (2,3,1), \emptyset,\emptyset, (2,1)\} \]

这样我们就构造出了长为 \(n\) 的排列到符合条件的 sif 排列序列的一个双射。\(\square\)

接下来就是标准处理方法了。作换元

\[A(x) = \frac{x}{G^{\langle -1 \rangle}(x)} \]

有

\[n! = [x^{n-1}] A^n(x) = [x^{n-1}] \left(\frac{x}{G^{\langle -1 \rangle}(x)}\right)^n = n [x^n]G(x) \]

即 \([x^n]G(x) = (n-1)!\)，这指出

\[G(x) = x\sum_{k\ge 0} k!x^k \]

复杂度瓶颈在求 \(G(x)\) 的复合逆。总实际复杂度 \(O(\text M(n) \log n)\)。

code

需要我的多项式板子。

signed main() {
	int n; cin >> n;
	poly G(n + 2); 
	rep(i,1,n + 1) G[i] = gfac(i - 1);
	G = G.composite_inv();
	rep(i,0,n) G[i] = G[i + 1]; G.resize(n + 1);
	G = G.inv();
	cout << G[n] << endl;
}

Reference:

[1] David Callan, Counting Stabilized-Interval-Free Permutations.
[2] Private conversation with jijidawang.