闲话 24.7.10

闲话

啊，zzz 真好玩啊！
慢热型，战斗非重点，美术风格超赞。如果不排斥米家 f2p 游戏，推荐大家玩一玩。
我是冲着妹妹去的

未来会补一些杨表公式的证明。现在先咕！

推歌：辰砂 by Licis et al. feat 洛天依AI

增补：另类杨图对应杨表计数

前置知识：杨表

什么是另类？不是一般的杨图，就是另类的杨图。这里的另类杨图有可能不是杨图，而只是一张和分拆有关的图。

记 \([n] = \{k\in\mathbb N \mid 1\le k \le n\}\)。

\(1.\) 形状的另类：移位图

\(\textbf{定义 1 } \text{(移位)}\)

一个分拆 \(\lambda\) 是严格的，当且仅当 \(\forall i, \lambda_i > \lambda_{i + 1}\)。对一个严格分拆 \(\lambda\)，定义形状为 \(\lambda\) 的移位（shifted）图为集合

\[D = [\lambda^*] = \{ (i, j) \mid 1\le i \le \ell(\lambda), i \le j \le \lambda_i + i - 1 \} \]

注意数列 \(\{\lambda_n + n - 1\}\) 是非严格递减的。

移位表的定义与杨表类似，对数字的限制相同，只是需要将其填入移位图。

例如，若 \(\lambda = (4, 3, 1)\)，那么移位图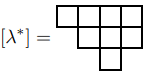

对严格分拆 \(\lambda\) 和它对应的移位图 \(D\)，令 \(\text{SYT}(D)\) 或 \(\text{SYT}(\lambda^*)\) 为形状为 \(D\) 的移位表，并令 \(g^\lambda = \lvert \text{SYT}(D) \rvert\)。

\(\textbf{定理 1 } \text{(I. Schur, 1911)}\)

对严格分拆 \(\lambda\)，有

\[g^\lambda = \frac{\lvert\lambda\rvert!}{\prod_{i = 1}^{\ell(\lambda)} \lambda_i!} \prod_{i < j} \frac{\lambda_i - \lambda_j}{\lambda_i + \lambda_j} \]

证明：繁。见 R. M. Thrall 的 A Combinatorial Problem。\(\square\)

为了得到移位图的钩长公式，我们得先有一个钩，还有它的钩长。但是这个钩长得就有点奇怪，更像是个篮子。

\(\textbf{定义 2 } \text{(移位钩)}\)

对严格分拆 \(\lambda\)，以及其移位图中的一个方格 \(c = (i, j) \in [\lambda^*]\)，定义其钩（hook）为

\[H_c^* = [\lambda^*] \cap \left(\{(i, j)\} \cup \{(i, j') \mid j' > j\} \cup \{(i', j) \mid i' > i\} \cup \{(j + 1, j') \mid j' \ge j + 1\} \right) \]

并定义其钩长为

\[h_c^* = \lvert H_c^* \rvert = \left\{\begin{aligned} &\lambda_i + \lambda_{j + 1}, & j < \ell(\lambda) \\ & \lambda_i - j + \left\lvert \{ i' \mid i' > i, \lambda_{i'} + i' \ge j + 1 \} \right\rvert, & j \ge \ell(\lambda) \end{aligned}\right. \]

只用符号会让眼花掉的。假设 \(\lambda = (5, 4, 2), c = (1, 2)\)，那么 \(H_c^*\) 便由 \(c\)、\(c\) 正下方的方格、\(c\) 正右方的方格和第 \(2 + 1 = 3\) 行中第 \(3\) 个及以后的方格组成。画出来就是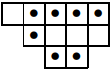

那么我们就能定义钩长公式了。

\(\textbf{定理 2 } \text{(移位钩长公式)}\)

对严格分拆 \(\lambda\)，有

\[g^\lambda = \frac{\lvert \lambda \rvert!}{\prod_{c\in [\lambda^*]} h_c^*} \]

证明：对每行的 \(c\) 分别展开可以发现，其等价于定理 \(1\)。\(\square\)

\(\textbf{定理 3 } \text{(移位行列式公式)}\)

令 \(\forall k < 0, (k!)^{-1} = 0\)。对严格分拆 \(\lambda\)，有

\[g^\lambda = \frac{\lvert \lambda \rvert!}{\prod_{i < j} (\lambda_i + \lambda_j)} \det \left\{ \frac{1}{\lambda_i - \ell(\lambda) + j}\right\}_{i, j=1}^{\ell(\lambda)} \]

证明：用与行列式公式类似的方式处理可以发现，其等价于定理 \(1\)。\(\square\)

\(2.\) 形状的限制：一些标准杨表

\(\text{(钩形)}\) 对分拆 \(\lambda\)，若 \(\forall 1 < i \le \ell(\lambda), \lambda_i = 1\)，则称 \(\lambda\) 和 \([\lambda]\) 是钩形的。图像上，其在左上角分成垂直的两条。

简记钩形分拆 \(\lambda = (n - k, 1, 1, \dots)\) 为 \((n - k, 1^k)\)。

对形状为某个钩形杨图 \((n - k, 1 ^k)\) 的杨表的计数是简单的。我们选出含 \(1\) 的 \(k + 1\) 个数顺序放在第一列，剩余的数依序放在第一行剩余空位。这样一个杨表就可以由从 \(2\sim n\) 选出的 \(k\) 个数唯一确定。也就是

\[f^{(n - k, 1^k)} = \binom{n - 1}{k} \]

从而，令 \(\lambda\) 枚举钩形分拆，我们有

\[\sum_{\lambda \vdash n} f^\lambda = \sum_{k} \binom{n - 1}{k} = 2^{n - 1} \]

我们也可以利用双射，将钩形杨表和 \([n]\) 的含 \(1\) 子集作一一对应（取第一行元素）。

\(\text{(两行形)}\) 对分拆 \(\lambda\)，若 \(\ell(\lambda) \le 2\)，则称 \(\lambda\) 和 \([\lambda]\) 是两行形的。图像上，其高度不超过 \(2\)。

在这里，我们要介绍一种杨表与投票（ballot）序列的映射关系，从而将杨表和格路建立联系，从而导出两行形杨表的计数。

一个正整数序列 \((a_1, \dots, a_n)\) 被称作投票序列，当且仅当对任意正整数 \(1\le k \le n\) 与任意 \(r\ge 1\)，有

\[\lvert \{ 1 \le i \le k \mid a_i = r \} \rvert \ge \lvert \{ 1 \le i \le k \mid a_i = r + 1 \} \rvert \]

也就是投票序列的每个前缀中，元素间出现次数大小的关系和元素大小关系相同。

投票序列其实抽象自这样一个情景：有 \(n\) 个人在给 \(m\) 个候选人投票，并令任意时刻，第 \(i\) 个候选人的得票数总多于第 \(i + 1\) 个候选人。\(a_i\) 就是第 \(i\) 个人所投票的候选人的编号。

考察 \(\lambda_r = \lvert \{ 1 \le i \le n \mid a_i = r \}\) 的 \(\lambda\)。根据上条件，\(\lambda\) 为一个 \(n\) 的分拆，这样我们称数列 \(\{a_n\}\) 的形状为分拆 \(\lambda\)。记所有形状为 \(\lambda\) 的投票序列为 \(\text{BS}(\lambda)\)。不加证明地，我们可以构造 \(\text{BS}(\lambda)\) 和 \(\text{SYT}(\lambda)\) 间的一个双射。令杨表为 \(D\)，对应的投票序列为 \(\{a_n\}\)，对每个 \(i\)，只需要让 \(a_i\) 为 \(D\) 中 \(i\) 所在方格的横坐标即可。

取一个投票序列 \(\{a_n\} \in \text{BS}(\lambda)\)，我们能由它唯一确定一条由 \((0, \dots, 0)\) 到 \((\lambda_1, \dots, \lambda_{\ell(\lambda)})\) 的 \(\ell(\lambda)\) 维格路。并且，知道这格路定被包含在一个锥形

\[\left\{\left.(x_1, \dots, x_{\ell(\lambda)}) \in \mathbb R^{\ell(\lambda)} \right\rvert x_1\ge \cdots \ge x_{\ell(\lambda)} \ge 0 \right\} \]

中。这样，我们就可以由一个杨表确定一条带限制格路了。若是斜杨表 \(D\in \text{SYT}(\lambda / \mu)\)，这条格路就是 \((\mu_1, \dots, \mu_{\ell(\lambda)}) \to (\lambda_1, \dots, \lambda_{\ell(\lambda)})\) 的。

现在，回到我们的两行形杨表，你是不是已经会了？

令我们的分拆是 \(\lambda = (n - k, k)\)，其中 \(k \le \lfloor n / 2\rfloor\)。根据上面的讨论，我们知道 \(f^\lambda = \lvert BS(\lambda)\rvert\)，即所有 \((0, 0) \to (n - k, k)\)，且不碰到 \(y = x + 1\) 的格路的计数。根据反射容斥，知道只需要计数所有 \((0, 0) \to (n - k, k)\) 的格路，再减去 \((0, 0) \to (n - k, k)\) 关于 \(y = x + 1\) 的对称点 \((k - 1, n - k + 1)\) 的格路。因此令 \(\binom{n}{-1} = 0\)，有

\[f^\lambda = \binom{n}{k} - \binom{n}{k - 1} \]

当 \(\lambda_1 = \lambda_2 = m\) 时即为 \(m\) 阶卡特兰数 \(C_m = \dfrac{1}{m + 1} \dbinom{2m}{m}\)。

从而，令 \(\lambda\) 枚举两行形分拆，我们有

\[\sum_{\lambda \vdash n} f^\lambda = \sum_{k = 0}^{\lfloor n / 2\rfloor} \binom{n}{k} - \binom{n}{k - 1} = \binom{n}{\lfloor n / 2\rfloor} \]

所有三行形的杨表的计数是 Motzkin 数。更高阶的计数参见 Enumeration of Standard Young Tableaux 的第 \(4\) 节。

\(\text{(之字形)}\) 对斜杨图 \(\lambda / \mu\)，若 \([\lambda / \mu]\) 四联通，且不存在 \(2\times 2\) 子方格，则其是之字形的。

之字形的英文是“zigzag shape”或“ring hook shape”，形状好像一条贪吃蛇。

那么我们该怎么最简要地确定一张之字形图呢？对一个 \(n\) 个方格的之字形图，考虑从左下角从 \(1\) 开始标号，并记录每个即将向上走的位置的标号，组成一个集合 \(S\subseteq [n - 1]\)。例如，\(n = 9, S = \{1, 3, 5, 6\}\) 导出的之字形图即为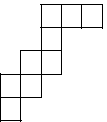

记由 \(n\) 和 \(S\) 唯一确定的斜杨图为 \(z_n(S)\)。我们下面要考虑 \(f^{z_n(S)}\) 的计算方法。

回顾之字形图的形状，我们惊喜地发现：每个方格最多和两个方格联通。这也就说明，方格内元素的关系可以被放在序列上说明。那么，需要什么样的序列呢？因为杨表填入的是 \(n\) 个不同的数字，我们自然会想到排列。取 \(\pi \in \mathcal S_n\)，并将其顺序（由左下角开始）填入 \(z_n(S)\)，那么

\[k\in S \iff \pi_i > \pi_{i + 1} \]

也就是说 \(S\) 标明了 \(\pi\) 的所有下降。记所有大小为 \(n\) 的斜杨表组成集合 \(Z_n\)，容易知道存在一个 \(Z_n\) 和 \(\mathcal S_n\) 的双射。因此有

\[\sum_{S \subseteq[n - 1]} f^{z_n(S)} = n! \]

那么，如果确定下了 \(S\)，我们又该如何计算 \(f^{z_n(S)}\) 呢？

这里我们就用排列的语言来说明了。考虑这问题相当于钦定了 \(\lvert S\rvert\) 个位置向上，而钦定问题一般要用容斥转化成任意。不妨固定 \(n\)，上升集为 \(S\) 的排列的计数为 \(f(S)\)，上升集是 \(S\) 的子集的排列的计数为 \(g(S)\)，那么据定义有

\[g(S) = \sum_{T\subseteq S} f(T) \]

根据容斥原理有

\[f(S) = \sum_{T \subseteq S}(-1)^{\lvert S\rvert - \lvert T\rvert} g(T) \]

我们知道，由于 \(g(S)\) 所计数的排列 \(\pi\) 不需要让每个 \(S\) 中的元素都标明一个下降，因此我们只需要让 \(S\) 的子排列内部递增即可。形式化地，令 \(S = \{s_1, \dots, s_k\}\)，并 \(1\le s_1 < \cdots < s_k \le n\)，那么我们只需要让 \(\pi_1 < \cdots < \pi_{s_1}\)，\(\pi_{s_1 + 1} < \cdots < \pi_{s_2}\)，\(\dots\)，\(\pi_{s_k} < \cdots < \pi_n\)。这限制是好满足的，我们只需要从 \([n]\) 中选出 \(s_1\) 个数顺序排列，再选出 \(s_2 - s_1\) 个数顺序排列，以此类推即可。因此有

\[g(S) = \binom{n}{s_1, s_2 - s_1, \dots, n - s_k} \]

因此，令 \(S = \{s_1, \dots, s_k\}\)，并 \(1\le s_1 < \cdots < s_k \le n\)，那么让 \(T = \{s_{i_1}, \dots, s_{i_j}\}\)，我们枚举 \(T\) 的元素，便有

\[f(S) = \sum_{1\le i_1 < \dots < i_j \le k} (-1)^{k - j} \binom{n}{s_{i_1}, s_{i_2} - s_{i_1}, \dots, n - s_{i_j}} \]

要把它化简，我们不如先暂停一下，转而思考一些更普遍的问题。取函数 \(f : [0, k + 1]^2 \to R\)，并令 \(\forall i, f(i, i) = 1\)，\(\forall i > j, f(i, j) = 0\)。我们断言

\[\sum_{1\le i_1 < \dots < i_j \le k} (-1)^{k - j} f(0, i_1) \cdots f(i_j, k + 1) = \det \begin{bmatrix} f(0, 1) &f(0, 2) &\cdots &f(0, k + 1) \\ f(1, 1) &f(1, 2) &\cdots &f(1, k + 1) \\ 0 &f(2, 2) &\cdots &f(2, k + 1) \\ \vdots &\vdots &\ddots &\vdots \\ 0 &0 &f(k, k) &f(k, k + 1) \\ \end{bmatrix}\]

RHS 矩阵为 \((i, j)\) 元为 \(f(i, j + 1)\) 的 Hessenberg 矩阵。

因此，我们令 \(f(i, j) = \dfrac{1}{(s_j - s_i)!}\)，其中 \(s_0 = 0, s_{k + 1} = n\) 即可使得上式的 \(\text{LHS}\times n!\) 满足 \(f(S)\) 的形式。因此我们知道

\[f^{z_n(S)} = n!\det\left\{\frac{1}{(s_{j + 1} - s_i)!}\right\}_{i, j = 0}^k \]

经过一些神秘的化简可以得到其等价于

\[f^{z_n(S)} = n!\det\left\{\binom{n - s_i}{s_{j + 1} - s_i}\right\}_{i, j = 0}^k \]

Reference

\([1]\): Ron M. Adin et al., Enumeration of Standard Young Tableaux
\([2]\): Richard P. Stanley, Enumerative Combinatorics.