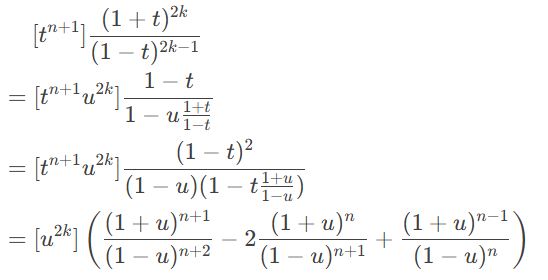闲话
怎么有人说了要补树上邻域数点但是天天打博德之门不补啊?是吧 gtm1514。
买到了咖啡炭烧味的酸奶。抽象
为啥没人看闲话了;;
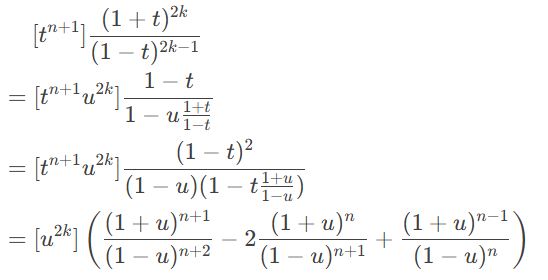
玄妙转化 from ℵ1022
但这个也就是 这个 的特殊情况吧?
推歌:Moonfall by 沉林川 feat. 诗岸
再见了啊 曾拥抱着我的月亮
你陪伴的每一个深夜啊
都不会 太冰凉
补题:新年的军队
最后还是来补了。当然本文基本复读 EI 题解,写的确实比较易懂。
没写有限微积分版本,纯 gf 推导。
文章最后有懒人版题解 /cy
U593
给定 \(n, m, k\)。定义长为 \(n\) 的排列 \(\pi\) 的一个下降是正整数 \(i < n\),使得 \(\pi_i > \pi_{i + 1}\)。对每个 \(1\le k'\le n\) 的 \(k'\),计数满足 \(\pi_k = k'\) 且恰有 \(m\) 个下降的长为 \(n\) 的排列 \(\pi\)。
\(n\le 5\times 10^5, 1\le k\le n, 0\le m \le n - 1\)。
看到这题面后想到的第一个结构大概是欧拉数,第二个结构没准是欧拉数的 bgf。
然后我们可能就已经意识到了,这题是 gf 科技题。事实的确如此。
随后我们会发现,恰有 \(m\) 个下降的性质易于用来在 gf 上区分不同的排列,但难以获得以该性质为基础的 gf。这的内核大概在于我们难以通过信息精简的 gf 表明每个元素是否已经出现。如果我们可以让选择某元素的可行性彼此独立,对下降的刻画就会变得相对简单。
如果想要达成这一点,我们就需要——稠密性。只要我们所刻画的对象是由稠密集里的元素组成的,那么“选择到两个相同元素”的概率就会无限趋近于 \(0\),这样我们要删除这种情况的难度就会无限小。
那么我们熟悉的哪个集合是稠密的呢?对啦!有理数集 实数集。至于为什么是实数集?因为概率密度函数总定义在实数集上。而这时排列的性质也可以自然地被刻画,我们只需要对 \(n\) 个实数离散化,得到的就是一个排列。
根据上面的思考,我们可以考虑概率密度扩充状态(咋用啊?)。记实数列 \(\alpha_1, \alpha_2, \dots, \alpha_n\) 为 \(\langle \alpha_n\rangle\),我们可以将问题转化为如下的等价形式:
定义实数列 \(\langle \alpha_n\rangle\) 的一个下降是正整数 \(i < n\),使得 \(\alpha_i > \alpha_{i + 1}\)。对每个 \(1\le k'\le n\) 的 \(k'\),计算满足 \(\alpha_k\) 的排名为 \(k'\) 且恰有 \(m\) 个下降的的实数列 \(\langle \alpha_n\rangle\) 的分布,其中 \(\langle \alpha_n\rangle\) 中每个元素都在 \([0, 1]\) 上均匀分布。
容易证明这转化和原问题等价,由于每个排列都可以被等概率地取到。同时,我们完美地规避了标记某元素是否被选择的问题。
处理其中某个 \(\alpha_k\) 时,我们可以将其视作随机变量,并使用概率密度函数刻画其分布。若实数列 \(\langle \alpha_n\rangle\) 中 \(\alpha_k\) 的排名为 \(r\),那么 \(\alpha_k = x\) 的概率密度即为 \(\dfrac{x^{r - 1}(1-x)^{n - r}}{(r - 1)!(n - r)!}\),考虑剩余 \(n - 1\) 个数的大小与其中大于/小于 \(\alpha_k\) 的数的排列顺序。
下面考虑加入元素对原来排列的概率密度函数的影响。设 \(f(x)\) 为实数列 \(\langle \alpha_n\rangle\) 关于 \(\alpha_n\) 的概率密度函数,则在 \(\langle \alpha_n\rangle\) 最后拼合一个 \(> \alpha_n\) / \(< \alpha_n\) 的元素 \(\alpha_{n + 1} = x\) 后 关于 \(\alpha_{n + 1}\) 的概率密度函数即 \(\int_0^x f(x) \mathrm dx\) / \(\int_x^1 f(x) \mathrm dx\)。
随后考虑如此刻画与原问题的转化。由于多项式的积分还是多项式,可以知道所讨论的概率密度函数都是多项式。假设 \(\langle \alpha_n\rangle\) 关于 \(\alpha_k\) 的概率密度函数为 \(f(x)\),并令该位置排名为 \(r\) 的方案数为 \(a_r\),则有
\[f(x) = \sum_{i = 0}^{n - 1} f_ix^i = \sum_{r = 0}^{n - 1}a_r \frac{x^{r}(1 - x)^{n - r - 1}}{r!(n - r - 1)!}
\]
EI 直接给出了上面式子的反演形式:
\[\sum_{r = 0}^{n - 1} \frac{a_r}{r!(n - r - 1)!}x^{r} = \sum_{k = 0}^{n - 1} f_k x^k(1 - x)^{n - k - 1}
\]
看上去就很对啊!那我先不证了。于是我们就可以先着手计算 \(f_k\),再考虑求出 RHS 的整个多项式。具体地,二项展开得到 RHS 就是
\[\sum_{k = 0}^{n - 1}x^k \sum_{i = 0}^k\binom{n - 1 - i}{k - i} f_i = \sum_{k = 0}^{n - 1} \frac{x^k}{(n - 1 - k)!} \sum_{i = 0}^k\frac{(n - 1 - i)! f_i}{(k - i)!}
\]
一次卷积即可。
接下来先把问题拆分。由于 \(\pi_k\) 的特殊性与加入元素位置的局限性,可以分别计算前 \(k-1\) 个元素与后 \(n - k\) 个元素对应的实数列关于末尾元素的概率密度函数,并拼合起来得到整个排列关于 \(\alpha_k\) 的概率密度函数。这过程只需要注意到排列的翻转会让上升与下降互相转换,分析一个部分即可。
令 \([u^nv^m]F(u,v,t)\) 为由 \(n\) 个上升,\(m\) 个下降组成的实数列关于其末尾的概率密度函数,其中 \(t\) 为变元。注意到 \(F(0, 0, t) = 1\),并由转移立得
\[F(t) = 1 + u\int_0^t F(x) \ \mathrm dx + v\int_t^1 F(t) \ \mathrm dt
\]
两侧对 \(t\) 微分得到 \(F'(t) = (u - v) F(t)\),这是一阶齐次线性微分方程,因此其解为
\[F(u, v, t) = Ce^{(u - v)t}
\]
随后确定常数,这 \(C\) 应当与 \(u, v\) 有关。令 \(I = \int_0^1 F(t) \mathrm dt\),则列出方程组
\[\left\{\begin{aligned} & 1 + uI = Ce^{u - v} \\ & 1 + vI = C\end{aligned}\right.
\]
解得
\[\left\{\begin{aligned} & C = \frac{u - v}{u - ve^{u - v}}\\ & F = \frac{\left(u - v\right)e^{(u - v)t}}{u - ve^{u - v}} \end{aligned}\right.
\]
随后令占位元 \(x\) 标明上升/下降总数量,\(y\) 标明下降数量,则前 \(n_1 = k - 1\) 个元素对应的实数列关于其末尾的概率密度函数关于下降的生成函数为 \([x^{n_1}]F(x, xy, t)\),后 \(n_2 = n - k\) 个元素对应的生成函数为 \([x^{n_2}]F(xy, x, t)\),这是由翻转决定的。而前 \(k\) 个元素组成的实数列对应 \(k - 1\) 个上升或下降,后 \(n - k + 1\) 个元素翻转组成的实数列对应 \(n - k\) 个上升或下降,并且这两个实数列末尾元素值相同,均为 \(\alpha_k\)。因此我们可以直接将对应的概率密度函数乘起来。
根据上面的讨论,不难发现 \(f(t)\) 对应的生成函数即为
\[\left([x^{n_1}]F(x, xy, t)\right)\left([x^{n_2}]F(xy, x, t)\right)
\]
而
\[\begin{aligned}
&[x^n] F(x, xy, t)
\\ = \ & [x^n] \frac{(1 - y)e^{x(1-y)t}}{1-ye^{x(1-y)}}
\\ = \ & [x^n] (1 - y)e^{x(1-y)t} \sum_{i\ge 0} e^{ix(1-y)} y^i
\\ = \ & (1 - y)\sum_{i\ge 0} \left([x^n] e^{(i + t)(1-y)x}\right) y^i
\\ = \ & (1 - y)^{n + 1}\sum_{i\ge 0} \frac{(i + t)^n}{n!} y^i
\end{aligned}\]
并且
\[\begin{aligned}
&[x^n] F(xy, x, t)
\\ = \ & [x^n] \frac{(y - 1)e^{x(y-1)(t-1)}}{1-ye^{x(1-y)}}
\\ = \ & [x^n] (y - 1)e^{x(y-1)(t-1)} \sum_{i\ge 0} e^{ix(1-y)} y^i
\\ = \ & (1 - y)\sum_{i\ge 0} \left([x^n] e^{(i - t + 1)(1-y)x}\right) y^i
\\ = \ & (1 - y)^{n + 1}\sum_{i\ge 0} \frac{(i - t + 1)^n}{n!} y^i
\end{aligned}\]
因此
\[\begin{aligned}
&\left([x^{n_1}]F(x, xy, t)\right)\left([x^{n_2}]F(xy, x, t)\right)
\\ = \ & \left((1 - y)^{n_1 + 1}\sum_{i\ge 0} \frac{(i + t)^{n_1}}{{n_1}!} y^i\right)\left((1 - y)^{{n_2} + 1}\sum_{i\ge 0} \frac{(i - t + 1)^{n_2}}{{n_2}!} y^i\right)
\\ = \ & \frac{1}{n_1!n_2!} (1 - y)^{n + 1} \left(\sum_{i\ge 0} (i + t)^{n_1} y^i\right)\left(\sum_{i\ge 0} (i - t + 1)^{n_2} y^i\right)
\end{aligned}\]
\(f_k\) 对应的生成函数即为上式的 \(y^m\) 次系数。到这里似乎就存在 \(O(n \log^2 n)\) 的插值做法了,但我不会 /dk
所以我们还是接着推吧。我喜欢生成函数,所以选 gf 推法。
\(f_k\) 对应的生成函数其实就是 \([ p^{n_1} q^{n_2}y^m] F(p, py, t) F(qy, q, t)\),展开得到
\[[ p^{n_1} q^{n_2}y^m] \frac{(1-y)^2\exp\left(pt(1-y) + q(1-t)(1-y)\right)}{\left(1 - ye^{p(1-y)}\right)\left(1 - ye^{q(1-y)}\right)}
\]
并且这就是
\[[p^{n_1} q^{n_2}y^m] \frac{(1-y)^{n + 1}\exp\left(pt + q(1-t)\right)}{\left(1 - ye^{p}\right)\left(1 - ye^{q}\right)}
\]
如果觉得不是很显然的话,可以看看上面只有 \(y,t\) 式子的最终形态。施分式分解(可以用 mma 的 Apart[, y] 函数)得到这就是
\[[p^{n_1} q^{n_2}y^m] (1-y)^{n + 1} \frac{\exp\left(pt + q(1-t)\right)}{e^p - e^q} \left(\frac{e^p}{1 - ye^p} - \frac{e^q}{1-ye^q}\right)
\]
但是这形式怎么看怎么难看。具体地,\(e^p - e^q\) 的常数项为 \(0\),我们没法直接对他求逆。但由于原式显然为形式幂级数,我们不能独立地看这一部分。
神秘操作:对 \(t\) 求导。得到
\[\begin{aligned}
&[p^{n_1} q^{n_2}y^m] (1-y)^{n + 1}\exp\left(pt + q(1-t) \right)\frac{p-q}{e^p - e^q} \left(\frac{e^p}{1 - ye^p} - \frac{e^q}{1-ye^q}\right)
\\ = \ & [p^{n_1} q^{n_2} y^m] (1-y)^{n + 1}\exp\left( (p-q)t \right)\frac{p-q}{e^{p-q} - 1} \left(\frac{e^p}{1 - ye^p} - \frac{e^q}{1-ye^q}\right)
\end{aligned}\]
我们神奇地发现了伯努利数的生成函数 \(B(x) = \dfrac{x}{e^x - 1}\) 的形式。由于分式分解得到的两部分分别只和 \(p,q\) 有关,讨论一部分对 \(y\) 的系数提取即可。这就是
\[\begin{aligned}
G(p) = \ & [y^m] (1-y)^{n + 1} \frac{e^p}{1 - ye^p}
\\ = \ & [y^m] \left(\sum_{i = 0}^{n + 1} (-1)^i \binom{n + 1}{i} y^i\right)\left(\sum_{i\ge 0} e^{(i + 1)p} y^i\right)
\\ = \ & \sum_{i = 0}^m (-1)^{m - i} \binom{n + 1}{m - i}e^{(i + 1)p}
\end{aligned}\]
原式即
\[[p^{n_1} q^{n_2}] e^{(p-q)t}B(p - q) \left(G(p) - G(q)\right)
\]
这是对称的。因此我们只需要处理两个部分:
第一部分:\([p^{n_1} q^{n_2}] e^{(p-q)t}B(p - q) G(p)\)。作换元 \(r = q/p\),原式即
\[\begin{aligned}
&[p^{n_1} (pr)^{n_2}] e^{(p-(pr))t}B(p - (pr)) G(p)
\\ = \ & [p^{n - 1} r^{n_2}] e^{p(1-r)t}B(p(1-r)) G(p)
\\ = \ & \sum_{j = 0}^{n-1} \left([p^{n - 1 - j}]G(p)\right) \left([p^jr^{n_2}]e^{p(1-r)t}B(p(1-r))\right)
\end{aligned}\]
由于后半部分可以被写成多项式复合 \(p(1-r)\) 的形式,可以知道 \(p^j\) 项的系数中 \(r\) 以 \((1-r)^j\) 的形式存在。因此
\[\begin{aligned}
\\ = \ & \sum_{j = 0}^{n-1} \left([p^{n - 1 - j}]G(p)\right) \left([r^{n_2}](1-r)^j\right)\left([p^j]e^{pt}B(p)\right)
\\ = \ & \sum_{j = 0}^{n-1} q_{n - 1 - j}\left([p^j]e^{pt}B(p)\right)
\\ = \ & \sum_{j = 0}^{n-1} \left([p^{n - 1 - j}] Q(p)\right)\left([p^j]e^{pt}B(p)\right)
\\ = \ & [p^{n - 1}]Q(p)B(p) e^{pt}
\\ = \ & \sum_{i = 0}^{n - 1} [p^{n - 1 - i}]Q(p)B(p) \frac{t^i}{i!}
\end{aligned}\]
其中
\[Q(p) = \sum_{i = 0}^{n - 1}q_i p^i = \left([p^{i}]G(p)\right) \left([r^{n_2}](1-r)^{n - 1 - i}\right) p^i
\]
第二部分:\([p^{n_1} q^{n_2}] e^{(p-q)t}B(p - q) G(q)\)。作换元 \(r = p/q\),原式即
\[\begin{aligned}
&[(qr)^{n_1} q^{n_2}] e^{((qr)-q)t}B((qr) - q) G(q)
\\ = \ & [q^{n - 1}r^{n_1}] e^{q(r-1)t}B(q(r - 1)) G(q)
\\ = \ & \sum_{j = 0}^{n-1} \left([q^{n - 1 - j}]G(q)\right) \left([q^jr^{n_1}]e^{q(r-1)t}B(q(r-1))\right)
\end{aligned}\]
\(q^j\) 项的系数中 \(r\) 以 \((r-1)^j\) 的形式存在。因此
\[\begin{aligned}
\\ = \ & \sum_{j = 0}^{n-1} \left([q^{n - 1 - j}]G(q)\right) \left([r^{n_1}](r-1)^j\right)\left([q^j]e^{qt}B(q)\right)
\\ = \ & \sum_{j = 0}^{n-1} d_{n - 1 - j}\left([p^j]e^{pt}B(p)\right)
\\ = \ & \sum_{i = 0}^{n - 1} [q^{n - 1 - i}]D(q)B(q) \frac{t^i}{i!}
\end{aligned}\]
其中
\[D(q) = \sum_{i = 0}^{n - 1}d_i q^i = \left([q^{i}]G(q)\right) \left([r^{n_1}](r-1)^{n - 1 - i}\right) q^i
\]
这样计算出来的 gf 是 \(f_k\) 对应的生成函数 \(F(x)\) 的导数。除了 \(f_0\) 外的数都好复原。但 \(f_0\) 呢?根据组合意义(?),我们(你们)知道 \(f_0\) 会平等地影响每一个 \(a_k\)。我们还知道 \(\sum a_k\) 应当为某欧拉数,因此只需要最后计算出这欧拉数减去目前的 \(\sum a_k\) 即可,只需将这一差值除 \(n\) 加入每个数。
最后一个问题就是如何计算 \(G(x)\) 的系数。
令 \(G(x) = e^x g(x) = e^x f(e^x)\),则
\[f(x) = \sum_{i = 0}^m (-1)^{m - i} \binom{n + 1}{m - i}x^i = (-1)^m\binom{n + 1}{m} {}_2F_1\left(\left.\begin{matrix}1,-m\\n+2-m\end{matrix}\right\rvert x\right)
\]
线性求算系数后再复合 \(e^x\) 即可做到 \(O(n\log^2 n)\) 的复杂度,但是跑的超级慢。能过就算赢!Sumbission
那不这么做了,还是抄写题解吧。
注意到
\[(n - m + 1 + i) f_i = (i - m - 1) f_{i - 1} + [i = 0] (n - m + 1)f_0
\]
令 \(C = (n - m + 1)f_0 = (-1)^m (n - m + 1) \dbinom{n + 1}{m}\),知道这就是
\[(n - m + 1)f + xf' = -mxf + x^2f' + C
\]
两侧复合 \(e^x\) 并求导得到
\[(n - m + 1)g + g' = -me^xg + e^xg' + C
\]
\[(n - m + e^x + me^x)g + (1 - e^x)(g + g') = C
\]
\[((n - m)e^{-x} + 1 + m)G + (e^{-x} - 1)G' = C
\]
提取系数得到
\[(n - m) \sum_{j = 0}^i \frac{(-1)^j}{j!}G_{i - j} + (m + 1)G_i + \sum_{j = 1}^i \frac{(-1)^j}{j!}(i - j + 1)G_{i - j + 1} = [i = 0]C
\]
把 \(G_i\) 单独拿出来可以得到
\[(n + 1 - i) G_i = [i = 0]C - (n - m)\sum_{j = 0}^{i - 1} \frac{(-1)^{i - j}}{(i - j)!} G_j - \sum_{j = 1}^{i - 1}\frac{(-1)^{i - j + 1}}{(i - j + 1)!} jG_j
\]
\[(n + 1 - i) G_i = [i = 0]C - \sum_{j = 0}^{i - 1} \left(\frac{(n - m)(-1)^{i - j}}{(i - j)!} + \frac{j(-1)^{i - j + 1}}{(i - j + 1)!}\right) G_j
\]
而 \(G_0\) 满足
\[(n + 1) G_0 = C
\]
那么就可以半在线卷积了。总时间复杂度是 \(O\left(\frac{n\log^2 n}{\log\log n}\right)\) 的。但我使用 fjzzq 的板子失败了。下面这段代码会递归爆栈,xdm 看看为什么 /kk
code
poly G_src(int n) {
pipeline g; poly a(n + 1), b(n + 1);
rep(i,0,n) {
if (i & 1) a[i] = - rfac[i], b[i] = rfac[i + 1];
else a[i] = rfac[i], b[i] = - rfac[i + 1];
}
mi C = (n - m + 1) * gC(n + 1, m);
if (m & 1) C = -C;
poly c(1); c[0] = C;
g.set(rfac[m + 1] * fac[m] * (c - (n - m) * a * g - b * gshl(gde(g), 1)));
return g.await(n + 1);
}
写了个 \(O(n\log^2 n)\) 的半在线卷积。因为退化了,不会写多叉。Submission。
tl;dr
令
\[G(x) = \sum_{i \ge 0} G_i x^i = \sum_{i = 0}^m (-1)^{m - i} \binom{n + 1}{m - i} e^{(i + 1)x}
\]
知道
\[((n - m)e^{-x}+1+m)G + (e^{-x}-1) G' = (-1)^m (n - m + 1) \binom{n + 1}{m}
\]
也就是
\[(n + 1 - i) G_i = [i = 0]C - \sum_{j = 0}^{i - 1} \left(\frac{(n - m)(-1)^{i - j}}{(i - j)!} + \frac{j(-1)^{i - j + 1}}{(i - j + 1)!}\right) G_j, \qquad G_0 = (-1)^m \frac{n - m + 1}{n + 1} \binom{n + 1}{m}
\]
使用半在线卷积即可 \(O(n\log^2 n)\) 或 \(O\left(\frac{n\log^2 n}{\log\log n}\right)\) 求解。
令
\[P(x) = \sum_{i = 0}^{n - 1} \left([q^{i}]G(q)\right) \left([r^{n_1}](r-1)^{n - 1 - i}\right) x^i, \quad Q(x) = \sum_{i = 0}^{n - 1} \left([p^{i}]G(p)\right) \left([r^{n_2}](1-r)^{n - 1 - i}\right) x^i, \quad B(x) = \frac{x}{e^x - 1}
\]
并令 \(f'(t) = [p^{n - 1}] B(p)Q(p) e^{pt} - [q^{n - 1}] B(q)P(q) e^{qt}\),我们可以自然还原出 \(f(t)\) 除常数项外的部分 \(f_1, f_2, \dots, f_{n - 1}\)。令 \(k'\) 对应的答案为 \(a_{k'- 1}\),则我们有
\[a_k = k!\sum_{i = 0}^k\frac{(n - 1 - i)! f_i}{(k - i)!}
\]
因此我们在不考虑 \(f_0\) 的情况下可以用上式以卷积的方式算出一列 \(a'_0, a'_1, \dots, a'_{n - 1}\)。由于真实的答案满足
\[\left\langle \begin{matrix} n \\ m \end{matrix} \right\rangle = \sum_{i = 0}^{n - 1} a_i
\]
而我们知道 \(f_0\) 对每个 \(a_i \leftarrow a'_i\) 的贡献相同,因此存在整数 \(b\) 使得
\[\sum_{i = 0}^{n - 1} \left( a_i - a'_i\right) = nb
\]
算出来 \(b\) 对答案修正即可。