基尼不纯度简介 - Gini Impurity

基尼不纯度Gini Impurity是理解决策树和随机森林分类算法的一个重要概念。我们先看看下面的一个简单例子 -

假如我们有以下的数据集

 

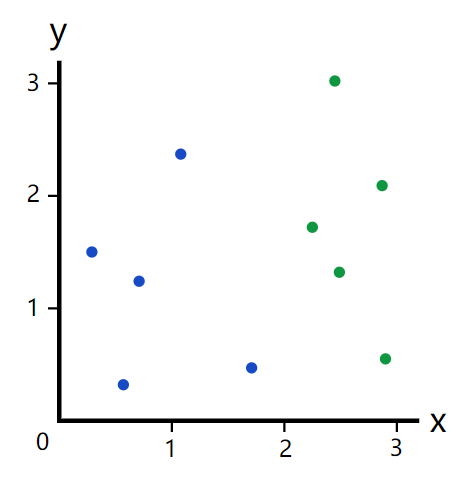
 我们如何选择一个很好的分割值把上面的5个蓝点和5个绿点完美的分开呢？通过观察，我们选择分隔值x=2

 

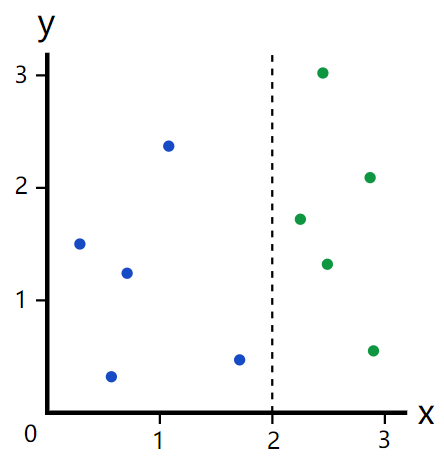
 如果我们选取x=1.5呢？

 

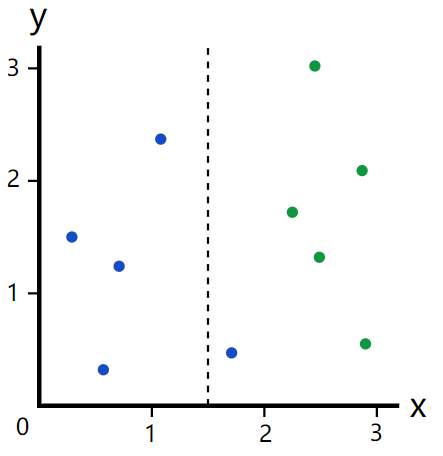
 这样做的结果是左边是4个蓝点，右边是5个绿点和1个蓝点。很显然，这种划分没有上面的好，可是我们如何定量地比较划分结果的好坏呢？

为了解决这个问题，人们引入了基尼不纯度这个概念，英文名称是Gini Impurity。接下来我们看看它是怎么计算出来的。

1. 随机从数据集中选出一个点

2. 计算数据集中数据分布概率：由于数据集中共有5个蓝点和5个绿点，所以随机选取的数据点有50%的可能性是蓝点，50%的可能性是绿点

3. 计算我们把上面随机选取的数据点分错类的概率（这个概率就是基尼不纯度Gini Impurity）：直觉告诉我们这个分错类的概率是0.5，因此使用随机分类的基尼不纯度就是0.5

这是一个最简单的情况，如果我们的数据集中有C个分类，一个数据点正好是第i个分类的概率是p(i)，那么计算基尼不纯度的公式就是

 

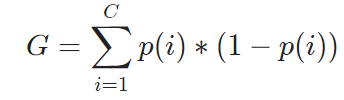
 使用这个公式计算前面随机分类的例子，我们还是得到同样的结果0.5

 

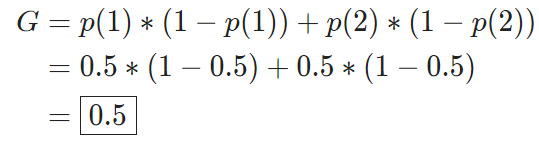
 如果我们使用x=2进行分类，相对应的基尼不纯度是多少呢？

 

使用x=2进行分类的决策树会有左右2给分支，左边有5个蓝点，右边有5个绿点。套用上面的公式，我们分别得到左右分支的基尼不纯度：

 

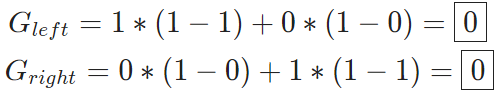
 因为这个一个完美的分类，因此这个不纯度为0，这也是最理想的分类结果。

我们再看看使用x=1.5进行分类的情况 -

因为左边分支只有4个蓝点，没有绿点，因此它的基尼不纯度为0；而右边分支有5个绿点1个蓝点，因此基尼不纯度为：

 

 

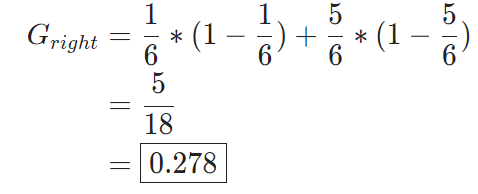
 有了上面的计算，我们应该如何选择最好的分类方法呢？

对应选择x=1.5的情况，我们知道在分类前的基尼不纯度为0.5，分类后左边分支为0，右边分支为0.278。如果我们考虑到2个分支各自拥有的数据点个数，我们得到一个加权平均值：

 

 跟分类前的基尼不纯度0.5相比，我们可以认为这个不纯度在分类后被降低了0.5 - 0.167 = 0.333，因此又把它称作基尼增益（Gini Gain）。基尼增益值越高，说明我们的分类效果越好。