C#快速排序算法实现及循环条件细节思考
C#快速排序算法实现及循环条件细节思考
快速排序是一种分治思想的递归排序算法,其基本思想为:
- 在每一步中,挑选一个主元(pivot)出来,比如第一个元素
- 然后遍历除主元外的剩下的元素,把所有小于主元的元素放在主元左边,把所有大于主元的元素放在主元右边,那么此时该主元元素所在的位置就是正确的位置,因为已经实现了所有左边的元素都比它小,所以有右边的元素都比它大
- 然后将数组分为两个子数组,分别是主元左边的所有比它小的元素组成的子数组,和右边的所有比它大的元素组成的子数组
- 对左右数组再进行上述步骤的操作,直至排序结束
实现左右相数组的相对顺序是通过交换实现的。
先上代码为敬:
public class QuickSort
{
private int[] arr;
public QuickSort(int[] array)
{
arr = array;
}
public virtual void Sort()
{
int size = arr.Length;
QuickSortUtil(arr, 0, size - 1);
}
private void Swap(int[] arr,int first,int second)
{
int temp = arr[first];
arr[first] = arr[second];
arr[second] = temp;
}
private void QuickSortUtil(int[] arr, int lower, int upper)
{
if (upper <= lower)
return;
int pivot = arr[lower];
int start = lower;//储存排序前的开端索引
int stop = upper;//储存排序前的尾端索引
while (lower < upper)
{
while(arr[lower]<=pivot && lower < upper) //此循环用来找到大于pivot的索引
{
lower++;
}
while(arr[upper]>pivot && lower <= upper)//此循环用来找到小于等于pivot的索引
{
upper--;
}
if (lower < upper)
Swap(arr, lower, upper);//如果上面两个循环都找到相应的索引,那么交换找到的两个索引对应的值
}
Swap(arr, upper, start);
QuickSortUtil(arr, start, upper - 1);
QuickSortUtil(arr, upper + 1, stop);
}
}
class Program
{
public static void Main()
{
int[] array = new int[] { 3, 4, 2, 1, 6, 5, 7, 8, 12, 1, 11, 4 };
QuickSort m = new QuickSort(array);
m.Sort();
foreach (var n in array)
Console.Write(n.ToString() + ",");
}
}
output:
1,1,2,3,4,4,5,6,7,8,11,12,
在代码中,有个细节问题,就是while外循环里的两个小的while循环的循环条件为什么一个是lower<upper,另一个是lower<=upper?
“天下大事,必作于细,天下难事,必作于易”,为了搞清楚这个细节,首先让我们看看最简单的情况,即上述代码对于已经排好序的数组,是如何起作用的,我们发现第一个小循环总是结束,不会执行,因为后面的元素都比它大(如果最小元素只有一个的话,没有重复),因此第一个小循环的作用就是在发现大于pivot的元素上停下来,同理,第二个小循环的作用就是在发现小于或者等于pivot的元素上停下来,然后交换两个元素的位置,那么,按照这样的逻辑,lower迟早与upper相遇,并且相遇时,lower处的元素一定是大于pivot的,而upper处的元素一定是不大于pivot的,那么关于lower<upper,lower<=upper的原因就在于这里,相遇时候的必然逻辑。
如下图:
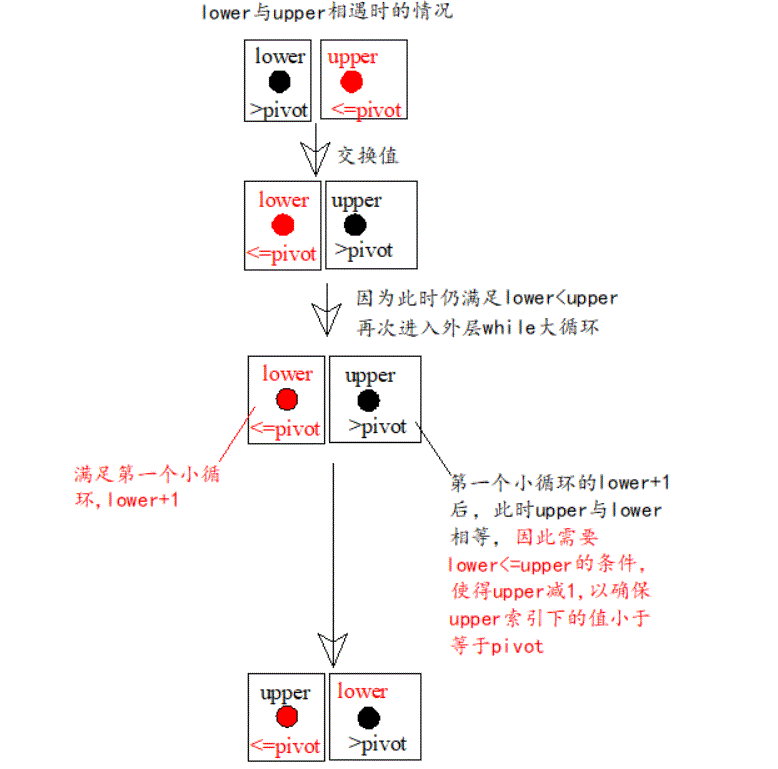
由此,可知,第二个小循环的lower <= upper中的等号存在的原因就是当lower与upper相遇时,lower在第一个小循环中自增了1,此时lower与upper相等,因此第二个小循环的lower<=upper才能使得upper自减1,确保每次退出大循环都是严格的upper<lower,而没有upper==lower的情况,如果有这种情况,那么就不能完全保证最后的upper下的元素是小于等于pivot的。
最后实际分析一个小例子,更形象:
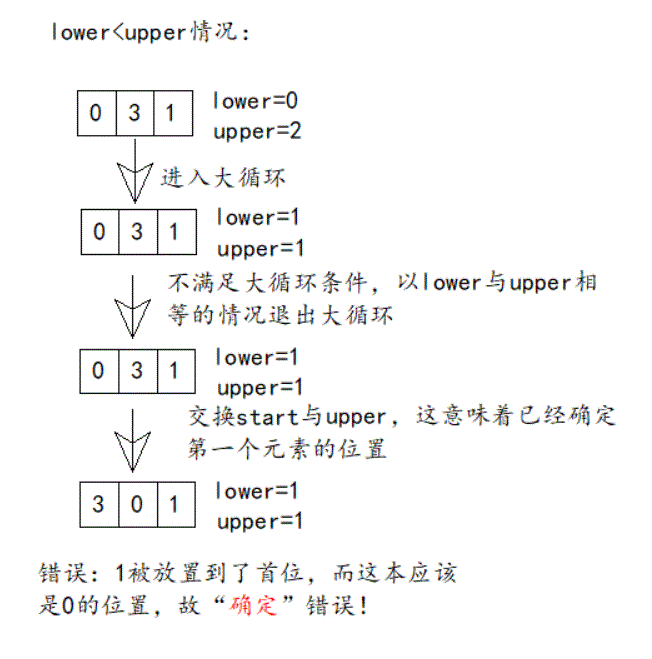

#####
愿你一寸一寸地攻城略地,一点一点地焕然一新
#####


 浙公网安备 33010602011771号
浙公网安备 33010602011771号