求最大的正整数n使满足n^2+2000n是完全平方数
将这一类题目汇集在一起
题目1：求最大的正整数n使满足n^2+2000n是完全平方数？
解：
讲问题更一般化，设Ａ=1000，当n^2+2An是完全平方数，求正整数n的值？
设平方数为m，则有：n^2+2An=m^2 （在本题目中A=1000）
n^2+2An+A^2-A^2=m^2
(n+A)^2 - A^2 = m^2
(n+A)^2 - m^2 = A^2
[(n+A)+m] [(n+A)-m] = A^2
设：
(n+A)+m = C 式子1
(n+A)-m = D 式子2
C * D = A^2
式子1 + 式子2 等于：
2(n + A) = C + D
求得： n = (C + D)/2 - A
如果想要n最大，必须 (C + D)/2 最大。并且C和D是A^2的两个因数。
在本题中 A = 1000
C * D = 1000*1000
C和D的可能值为(1000*1000 , 1) ,(1000*1000/2 , 2) ,(1000*1000/4 , 4) ,(1000*1000/5 , 5) ,(1000*1000/8 , 8) ,(1000*1000/10 ,10) ......
当 D =1 ， C = (1000 * 1000) 时，(C + D)/2 (C + D)/2最大，但不是整数。[注1]
只有当 D = 2 ， C = (1000 * 1000)/ 2 时，(C + D)/2 为正整数 ,并且(C + D)/2最大：
(C + D)/2 = [ (1000 * 1000)/ 2 + 2 ] /2 。
故 n = [ (1000 * 1000)/ 2 + 2 ] /2 -1000 = 500^2 + 1 - 1000
解得当 n= 249001 时，n是最大的正整数，使的 n^2+2000n 是完全平方数
题目2：求使n^2+1997n是一个完全平方数的最大正整数n的值
解：
将问题一般化，设：A是个质数。（本题中A=1997），求使n^2+An是一个完全平方数的最大正整数n的值
n^2+An=m^2
4n^2+2(2n)A=4m^2
(2n)^2 +2(2n)A + A^2 = (2m)^2 + A^2
(2n+A)^2 - (2m)^2 = A^2
[(2n+A) + 2m] [ (2n+A) - 2m] = A^2
设：C=[(2n+A) + 2m] , D= [ (2n+A) - 2m]
C * D = A^2
C+D=[(2n+A) + 2m] + [ (2n+A) - 2m] = 2(2n＋A)
n = [(C+D)/2-A]/2
如果想要n最大，必须 (C + D)/2 最大。并且C和D是A^2的两个因数。（因为C * D = A^2）
当C = A^2 & D = 1 时，(C+D)最大，为1+A^2,且(C+D)/2为整数。[解释看注1]
本题中 A=1997 & C+D = 1997*1997 +1
n = [(C+D)/2-A]/2
n =［（1997*1997 +1）/2－1997］/2 = ［（3988009 +1）/2－1997］/2 =［（3988010）/2－1997］/2= (1994005－1997)/2 = 1992008/2 =996004 (是整数)
则：n=996004时，是使n^2+1997n是一个完全平方数的最大正整数n的值
题目3：已知n^2+15n+26是一个完全平方数，求n的值？
简单解：
n^2+15n+26 =(n+13)(n+2)
设：
n+13=a^2
n+2=b^2
两式子相减：
a^2-b^2 = 11
(a+b)(a-b) = 11*1
a+b = 11
a-b = 1
a=6
n+13=6*6
则：n=23
[注1] 的解释：
题目4 已知 c*d=A(c,d,A均为正整数， A>1),求在[1，A]区间中，c+d 的最大值。
解：
由不等式 c+d >= 2*(c*d)^(1/2)
当c = d 时， c+d有最小值2*(A)^(1/2)。故函数y=c+d,当
c=d=(A)^(1/2)时，y有最小值是2*(A)^(1/2)。
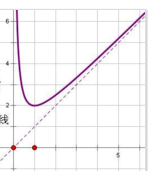
函数y=c+d = c + A/c 是双钩函数
函数y在c取值 0<c<(A)^(1/2)时，是单调递减的：证明参见附录
函数y在c 的取值(A)^(1/2) <c<正无穷 时，是单调递增的：证明参见附录
又因为c=A，y=A+1 & c=1 y=1+A
1 <c=(A)^(1/2) 并且 c=(A)^(1/2)<A
y的最小值点，c的取值在闭[1，A]区间中，
故在闭[1，A]区间中，c = A 或 c=1 时，y=c+d有极大值1+A
附录：
题目：f(x) = x+ A/x ,A>1 ，x>0 ,分析函数f的单调性。
解：设e>0
f(x+e)- f(x) = [x+e + A/(x+e)]–(x+A/x)
=e+A*[1/(x+e) – 1/x)=e{1-A/[x*(x+e)]}
当x>A^(1/2)
{1-A/[x*(x+e)]}>0
f(x+e)- f(x) >0 ,函数f(x)是递增的。
当0<x<A^(1/2)
{1-A/[x*(x+e)]}<0
f(x+e)- f(x) <0 ,函数f(x)是递减的。
