数据结构之环形队列
概述
队列是一种具有先进先出（FIFO）的数据类型，可以使用多种数据结构来实现队列：数组和链表。
简单队列的应用场景比较有限，于是那些牛人们就发明一些复杂的队列：
- 环形队列
- 双端队列
- 优先队列
应用场景
- Memory Management: The unused memory locations in the case of ordinary queues can be utilized in circular queues.
- Traffic system: In computer controlled traffic system, circular queues are used to switch on the traffic lights one by one repeatedly as per the time set.
- CPU Scheduling: Operating systems often maintain a queue of processes that are ready to execute or that are waiting for a particular event to occur.
- Lock Free Queue: When high performance is required, we don’t want to use lock. Circular Queue can is the top 1 data structure for lock free queue.
一般应用于需要高效且频繁进行多线程通信传递数据的场景，例如：Linux捕包、发包等等，（Linux系统中对PACKET_RX_RING和PACKET_TX_RING的支持实质就是内核实现的一种环形队列），或者用于在进程间的异步数据传输或记录日志文件时，为解决某些特殊情况下的竞争问题提供一种免锁的方法。
分析
Circular Queue，环形缓冲区，RingBuffer，先进先出，提供对缓冲区的互斥访问，通常有一个读指针和写指针。实际环形队列在工作时有3种情况：
- 入队速度=出队速度
一般情况，即入队速度和出队速度大致一样，即使某个突然时刻入队速度陡然变高或者出队速度陡然变低，都能通过队列这个缓冲区把这些数据先存起来，等到能处理的时候再处理。
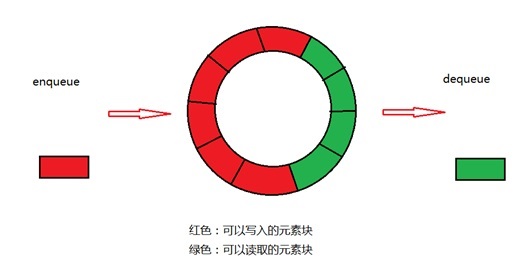
- 入队速度>出队速度
队列写入的速度>读取的速度，一段时间后，队列中大多数全是写入但没读取的元素，当又一个新的元素产生时，可以把这个新元素drop掉或者放在另一个缓冲区保存起来，此时说明你需要对出队处理元素的算法或逻辑优化处理速度。
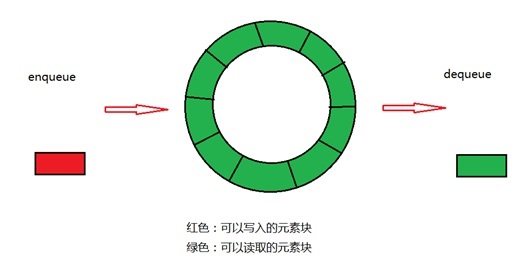
- 入队速度<出队速度
队列读取速度>写入速度，说明程序出队处理元素的速度很快，这是比较好的情况，不足之处：读取队列时可能经常会轮询队列是否有新的元素，造成cpu占用过高。
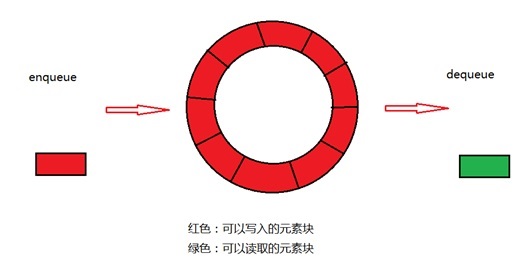
引申
引入环形队列，为了解决什么问题？？
顺序队列的假溢出问题：队列的存储空间未满，却发生溢出。比如 rear 现在虽然指向最后一个位置的下一位置，但是之前队头也删除一些元素，队头指针经历若干次的 +1 之后，遗留下很多空位置，但是顺序队列还在傻乎乎的以为再有元素入队，就溢出呢！肯定不合理。故循环队列诞生！
有两种可行的解决方法：
- 平移元素：把元素平移到队列的首部。效率低。否决
- 将新元素插入到第一个位置上，构成循环队列，入队和出队仍按先进先出的原则进行。操作效率高、空间利用率高。
使用循环队列解决假溢出问题，但引入新问题：判空。
满足front = rear条件的队列有两种情况：队列空和队列满：
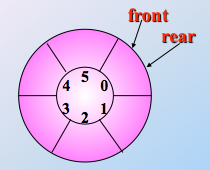
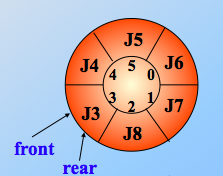
解决办法：
- 另设一个布尔变量以区别队列的空和满；
- 少用一个元素的空间，约定入队前测试尾指针在循环下加 1 后是否等于头指针，若相等则认为队满；（常用）
- 使用一个计数器记录队列中元素的总数。
实现
C参考实现GitHub
环形队列可使用数组或链表来实现，一般很少用链表来实现，因为访问链表需要挨个遍历。
需要维护两个属性，即2个index，一个是写入index，标示当前可以写入元素的index，入队时使用。一个是读取index，标示当前可以读取元素的index，出队时使用。
另外，节点状态的切换也是一个问题，即当前节点是可读还是可写。解决方案：在队列中每个元素的头部加一个元素标示字段，标示这个元素是可读还是可写，而这个的关键就在于何时设置元素的可读可写状态，当这个元素读取完之后，要设置可写状态，当这个元素写入完成之后，要设置可读状态。
public class RingBuffer {
/**
* 最大总量
*/
private final int maxSize;
/**
* 表示队列的第一个元素的位置,初始值默认为0
*/
private int front;
/**
* 表示队列的最后一个元素的后一个位置,初始值默认为0,需要空出一个空间作为“约定”
*/
private int rear;
/**
* 存放数据用的数组队列
*/
private final int[] queueArray;
/**
* 初始化一个maxSize长度的数组队列。
*/
public RingBuffer(int maxSize) {
this.maxSize = maxSize;
this.queueArray = new int[maxSize];
}
/**
* 判断队列是否满
*/
public boolean isFull() {
return (rear + 1) % maxSize == front;
}
/**
* 判断队列是否为空
*/
public boolean isEmpty() {
return rear == front;
}
/**
* 往队列中添加一个元素
*/
public boolean addQueue(int element) {
if (isFull()) {
return false;
}
// 队尾后移一位
queueArray[rear] = element;
rear = (rear + 1) % maxSize;
return true;
}
/**
* @return 弹出&获取当前队首任务
*/
public int takeQueue() {
if (isEmpty()) {
throw new RuntimeException("队列为空");
}
// 队首后移一位
int value = queueArray[front];
queueArray[front] = 0;
front = (front + 1) % maxSize;
return value;
}
/**
* 显示队列里的数据
*/
public void showQueue() {
if (isEmpty()) {
System.out.println("队列里没有数据");
return;
}
for (int i = front; i < front + size(); i++) {
System.out.println("当前数据顺序位数 = " + queueArray[i]);
}
}
/**
* @return 队列中有效数据个数
*/
public int size() {
return (rear + maxSize - front) % maxSize;
}
public static void main(String[] args) {
int size = 10;
RingBuffer ringBuffer = new RingBuffer(size);
for (int i = 0; i < size; i++) {
boolean success = ringBuffer.addQueue(i);
System.out.println(success ? "插入" + i + "成功" : "插入" + i + "失败");
}
for (int i = 0; i < size + 1; i++) {
if (i == size - 1) {
int item = ringBuffer.takeQueue();
System.out.println("取出" + item + "成功");
}
if (i == size) {
int item = ringBuffer.takeQueue();
System.out.println("取出" + item + "成功");
}
boolean putSuccess = ringBuffer.addQueue(i);
// 只有在i=9和10时才会各读取一次,所以这里的插入大部分都会失败,因为前面写入一轮缓冲区已经满
System.out.println(putSuccess ? "插入" + i + "成功" : "插入" + i + "失败");
}
}
}
输出：
插入0成功
插入1成功
插入2成功
插入3成功
插入4成功
插入5成功
插入6成功
插入7成功
插入8成功
插入9失败
插入0失败
插入1失败
插入2失败
插入3失败
插入4失败
插入5失败
插入6失败
插入7失败
插入8失败
取出0成功
插入9成功
取出1成功
插入10成功
Process finished with exit code 0
