迪杰斯特拉算法
前言
复习计算机网络, 这里总结一下迪杰斯特拉算法过程, 方便复习.
迪杰斯特拉算法过程
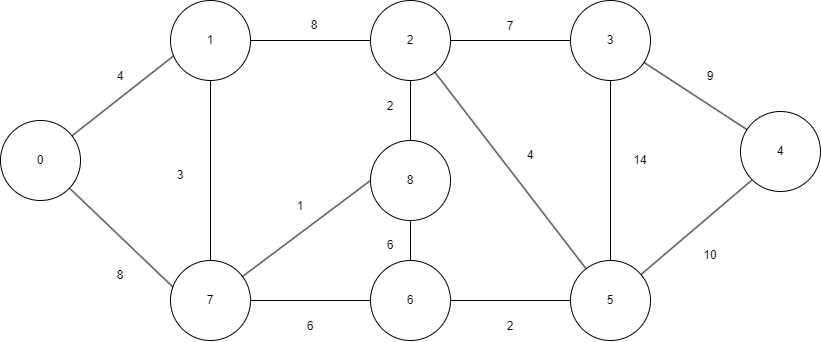
表格中 "step" 代表算法代表第几步, Node代表目前已经求出的最短路径的节点, 每一步都更新一遍所有节点的最短的路径的值(∞代表没走到那个节点), 并确定一个路径最短的节点, 画下划线的是已经求出全局路径最小的节点.
| step | Node | D(1),P(1) | D(2),P(2) | D(3),P(3) | D(4),P(4) | D(5),P(5) | D(6),P(6) | D(7),P(7) | D(8),P(8) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | (4, 0) | ∞ | ∞ | ∞ | ∞ | ∞ | (8, 0) | ∞ |
第一步, 从0节点开始, 只可以到达节点1和节点7, 最选出最短的节点1.
| step | Node | D(1),P(1) | D(2),P(2) | D(3),P(3) | D(4),P(4) | D(5),P(5) | D(6),P(6) | D(7),P(7) | D(8),P(8) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | (4, 0) | ∞ | ∞ | ∞ | ∞ | ∞ | (8, 0) | ∞ |
| 2 | 0, 1 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | ∞ | (7, 1) | ∞ |
第二步, 从节点1开始, 只可到达节点2和节点7, 通过 0 -> 1 -> 7 路径为7, 比路径8更短, 更新节点7的值, 并选出最短的节点7.
| step | Node | D(1),P(1) | D(2),P(2) | D(3),P(3) | D(4),P(4) | D(5),P(5) | D(6),P(6) | D(7),P(7) | D(8),P(8) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | (4, 0) | ∞ | ∞ | ∞ | ∞ | ∞ | (8, 0) | ∞ |
| 2 | 0, 1 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | ∞ | (7, 1) | ∞ |
| 3 | 0, 1, 7 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | (13, 7) | (7, 1) | (8, 7) |
第三步, 从节点7开始, 只可到达节点6和节点8, 选出最短的节点8.
| step | Node | D(1),P(1) | D(2),P(2) | D(3),P(3) | D(4),P(4) | D(5),P(5) | D(6),P(6) | D(7),P(7) | D(8),P(8) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | (4, 0) | ∞ | ∞ | ∞ | ∞ | ∞ | (8, 0) | ∞ |
| 2 | 0, 1 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | ∞ | (7, 1) | ∞ |
| 3 | 0, 1, 7 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | (13, 7) | (7, 1) | (8, 7) |
| 4 | 0, 1, 7, 8 | (4, 0) | (10, 8) | ∞ | ∞ | ∞ | (13, 7) | (7, 1) | (8, 7) |
第四步, 从节点8开始, 只可到达节点2和节点6, 选出最短的节点2.
| step | Node | D(1),P(1) | D(2),P(2) | D(3),P(3) | D(4),P(4) | D(5),P(5) | D(6),P(6) | D(7),P(7) | D(8),P(8) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | (4, 0) | ∞ | ∞ | ∞ | ∞ | ∞ | (8, 0) | ∞ |
| 2 | 0, 1 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | ∞ | (7, 1) | ∞ |
| 3 | 0, 1, 7 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | (13, 7) | (7, 1) | (8, 7) |
| 4 | 0, 1, 7, 8 | (4, 0) | (10, 8) | ∞ | ∞ | ∞ | (13, 7) | (7, 1) | (8, 7) |
| 5 | 0, 1, 7, 8, 2 | (4, 0) | (10, 8) | (17, 2) | ∞ | (14, 2) | (13, 7) | (7, 1) | (8, 7) |
第五步, 从节点2开始, 只可到达节点3和节点5, 选出最短的节点6.
| step | Node | D(1),P(1) | D(2),P(2) | D(3),P(3) | D(4),P(4) | D(5),P(5) | D(6),P(6) | D(7),P(7) | D(8),P(8) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | (4, 0) | ∞ | ∞ | ∞ | ∞ | ∞ | (8, 0) | ∞ |
| 2 | 0, 1 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | ∞ | (7, 1) | ∞ |
| 3 | 0, 1, 7 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | (13, 7) | (7, 1) | (8, 7) |
| 4 | 0, 1, 7, 8 | (4, 0) | (10, 8) | ∞ | ∞ | ∞ | (13, 7) | (7, 1) | (8, 7) |
| 5 | 0, 1, 7, 8, 2 | (4, 0) | (10, 8) | (17, 2) | ∞ | (14, 2) | (13, 7) | (7, 1) | (8, 7) |
| 6 | 0, 1, 7, 8, 2, 6 | (4, 0) | (10, 8) | (17, 2) | ∞ | (14, 2) | (13, 7) | (7, 1) | (8, 7) |
第六步, 从节点6开始, 可到达节点5, 选出最短的节点5.
| step | Node | D(1),P(1) | D(2),P(2) | D(3),P(3) | D(4),P(4) | D(5),P(5) | D(6),P(6) | D(7),P(7) | D(8),P(8) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | (4, 0) | ∞ | ∞ | ∞ | ∞ | ∞ | (8, 0) | ∞ |
| 2 | 0, 1 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | ∞ | (7, 1) | ∞ |
| 3 | 0, 1, 7 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | (13, 7) | (7, 1) | (8, 7) |
| 4 | 0, 1, 7, 8 | (4, 0) | (10, 8) | ∞ | ∞ | ∞ | (13, 7) | (7, 1) | (8, 7) |
| 5 | 0, 1, 7, 8, 2 | (4, 0) | (10, 8) | (17, 2) | ∞ | (14, 2) | (13, 7) | (7, 1) | (8, 7) |
| 6 | 0, 1, 7, 8, 2, 6 | (4, 0) | (10, 8) | (17, 2) | ∞ | (14, 2) | (13, 7) | (7, 1) | (8, 7) |
| 7 | 0, 1, 7, 8, 2, 6, 5 | (4, 0) | (10, 8) | (17, 2) | (24, 5) | (14, 2) | (13, 7) | (7, 1) | (8, 7) |
第七步, 从节点5开始, 可到达节点3和节点4, 选出最短的节点3.
| step | Node | D(1),P(1) | D(2),P(2) | D(3),P(3) | D(4),P(4) | D(5),P(5) | D(6),P(6) | D(7),P(7) | D(8),P(8) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | (4, 0) | ∞ | ∞ | ∞ | ∞ | ∞ | (8, 0) | ∞ |
| 2 | 0, 1 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | ∞ | (7, 1) | ∞ |
| 3 | 0, 1, 7 | (4, 0) | (12, 1) | ∞ | ∞ | ∞ | (13, 7) | (7, 1) | (8, 7) |
| 4 | 0, 1, 7, 8 | (4, 0) | (10, 8) | ∞ | ∞ | ∞ | (13, 7) | (7, 1) | (8, 7) |
| 5 | 0, 1, 7, 8, 2 | (4, 0) | (10, 8) | (17, 2) | ∞ | (14, 2) | (13, 7) | (7, 1) | (8, 7) |
| 6 | 0, 1, 7, 8, 2, 6 | (4, 0) | (10, 8) | (17, 2) | ∞ | (14, 2) | (13, 7) | (7, 1) | (8, 7) |
| 7 | 0, 1, 7, 8, 2, 6, 5 | (4, 0) | (10, 8) | (17, 2) | (24, 5) | (14, 2) | (13, 7) | (7, 1) | (8, 7) |
| 8 | 0, 1, 7, 8, 2, 6, 5, 3 | (4, 0) | (10, 8) | (17, 2) | (24, 5) | (14, 2) | (13, 7) | (7, 1) | (8, 7) |
第八步, 从节点3开始, 可以到达节点4, 选出最后一个节点: 节点4.
