递归
- 递归模式:
多递归基:为保证有穷性,递归算法都必须设置递归基,且确保总能执行到。为此,针对每一类可能出现的平凡情况,都需设置对应的递归基,故同一算法的递归基可能(显式或隐式的不止一种);
例如:数组倒置问题:
void reverse (int *,int,int); void reverse (int * A, int n){ reverse(A,0,n-1); } void reverse (int * A, int l, int r){ if ( l < r ) {//递归基可能是l=r或者l>r swap(A[l],A[r]); reverse(A, l+1, r-1); } }
多向递归:递归调用可能有多种可供选择的分支
例如:计算幂函数 。按照线性递归的构思,该函数可重新定义如下:
。按照线性递归的构思,该函数可重新定义如下:
 。按照线性递归的构思,该函数可重新定义如下:
。按照线性递归的构思,该函数可重新定义如下:
若从其他角度分析,可给出:

一般的,若n的二进制展开式为: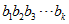 ,则:
,则: ,
,
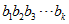 ,则:
,则: ,
,若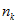 和
和 的二进制展开式分别为:
的二进制展开式分别为: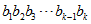 和
和 ,则有:
,则有:
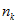 和
和 的二进制展开式分别为:
的二进制展开式分别为: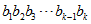 和
和 ,则有:
,则有: ,
,由此,可归纳得如下递推式:
 ,
,基于这一递归式,有如下多项递归版本:
inline __int64 sqr( __int64 a ) { return a * a ; } __int64 power2_re ( __int64 n ) { if ( n == 0) { return 1; } return ( n & 1) ? sqr ( power2_re( n >> 1)) * 2 : sqr ( power2_re( n >> 1)); }
上述递归算法的时间复杂度为: ,因为每次递归调用入参均缩小一半
,因为每次递归调用入参均缩小一半
 ,因为每次递归调用入参均缩小一半
,因为每次递归调用入参均缩小一半


