Frequency-domain adaptive Kalman filter for acoustic echo control in hands-free telephones(频域卡尔曼滤波器)

1. 本文介绍

本文组织如下：在第 2 节中，我们将重新审视回声消除器和后置滤波器的概念，并推导出这种双自适应滤波器结构的维纳解。在第 3 节中，我们将介绍频域中时变回波路径的随机状态空间模型。在第 4 节中，我们将在 DFT 域中开发一个有效版本的卡尔曼滤波器，在第 5 节中，我们将把它分解为数字信号处理的标准组件。第 6 节评估了现实条件下的算法性能，本文的结论将在第 7 节中得出。

2. 重新审视回声消除器和后置滤波器

2.1 免提通信系统的统计模型

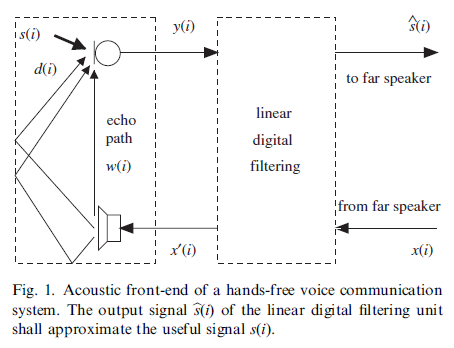
麦克风接收信号$y(i)$:

$$\begin{aligned}
y(i) &=s(i)+d(i) \\
&=s(i)+w(i) * x(i) \\
&=s(i)+\sum_{p} w(p) x(i-p)
\end{aligned}$$

由于语音信号$s(i)$不能单独观察，它被建模为具有零均值和自相关为$\varphi_{s s}(n)=\mathscr{E}\{s(i) s(i+n)\}$的平稳随机过程。附加回声信号$d(i)$由可测量（即确定性）扬声器信号$x(i)$和未知回声路径系数$w(i)$的线性卷积给出。由于声学回声路径的这种不确定性，系数序列$w(i)$被建模为具有统计期望$w_{0}(i)$和协方差$\varphi_{w_{r} w_{r}}(n)$的独立随机过程：

$$\begin{array}{l}
w_{o}(i)=\mathscr{E}\{w(i)\} \\
w_{r}(i)=w(i)-w_{o}(i) \\
\varphi_{w_{r} w_{r}}(n)=\mathscr{E}\left\{w_{r}(i) w_{r}(i+n)\right\}
\end{array}$$

麦克风输出信号$\widehat{s}(i)$作为输入信号$x(i)$和$y(i)$的线性组合：

$$\begin{aligned}
\widehat{s}(i) &=w_{2}^{\prime}(i) * y(i)+w_{1}^{\prime}(i) * x(i) \\
&=w_{2}(i) *\left[y(i)-w_{1}(i) * x(i)\right] \\
&=w_{2}(i) * e(i)
\end{aligned}$$

我们将$w_{1}(i)$称为回声消除器，将$w_{2}(i)$称为用于残余回声抑制的后置滤波器。$e(i)=y(i)-w_{1}(i)*x(i)$意味着回声消除后的错误信号。

2.2 广义维纳解

3. 回波路径的随机状态空间建模

4. 频域自适应卡尔曼滤波器

4.1 条件均值和协方差的精确卡尔曼滤波器

4.2 近似值

这里提出的近似值主要基于这样的假设，即 DFT 以足够的精度对协方差矩阵进行对角化。一般来说，如果向量长度和矩阵维度覆盖了相关信号的相关跨度，这个假设是合理的。如果我们确保满足这一点，近似值与可以实现的巨大简化相比，相关的算法降级很小。首先，观测噪声$\mathbf{S}(k)=\mathbf{F}_{M} \mathbf{Q s}(k)$和过程噪声$\Delta \mathbf{W}(k)$的协方差矩阵的近似：

$$\begin{array}{l}
\boldsymbol{\Psi}_{s s}(k) \approx R \cdot \operatorname{diag}\left\{\boldsymbol{\Phi}_{s s}(k)\right\} \\
\boldsymbol{\Psi}_{\Delta \Delta}(k) \approx M \cdot \operatorname{diag}\left\{\boldsymbol{\Phi}_{\Delta \Delta}(k)\right\}
\end{array}$$